
- •XII. Обыкновенные дифференциальные уравнения
- •1. Определение дифференциального уравнения. Задача Коши
- •2. Уравнение с разделяющимися переменными
- •3. Однородные дифференциальные уравнения
- •4. Линейные дифференциальные уравнения первого порядка
- •5. Уравнение Бернулли
- •6. Уравнение в полных дифференциалах
- •7. Дифференциальные уравнения, допускающие понижение порядка
- •8. Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами
- •9. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами
- •10. Метод вариации постоянных
- •11. Задачи, приводящие к дифференциальным уравнениям
- •12. Системы дифференциальных уравнений. Линейные системы
- •13. Линейные однородные системы с постоянными коэффициентами
- •14. Линейные неоднородные системы дифференциальных уравнений
- •Задание 12.1
- •Задание 12.11
- •Задание 12.12
- •Библиографический список
- •Бородицкий м.П., Каибханов к.Э.,
XII. Обыкновенные дифференциальные уравнения
1. Определение дифференциального уравнения. Задача Коши
Обыкновенным дифференциальным уравнением называется уравнение
![]() (1)
(1)
связывающее
независимое переменное x,
искомую функцию
![]() и ее производные
и ее производные![]() .
.
Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Функция ![]() называется (частным) решением
дифференциального уравнения (1), если
называется (частным) решением
дифференциального уравнения (1), если![]() .
Уравнение (1) имеет, как правило,
бесчисленное множество решений. Общим
решением уравнения (1) называется
семейство функций
.
Уравнение (1) имеет, как правило,
бесчисленное множество решений. Общим
решением уравнения (1) называется
семейство функций![]() ,
зависящих отn
параметров
,
зависящих отn
параметров
![]() ,
таких, что для любого допустимого набора
,
таких, что для любого допустимого набора![]() получается частное решение
получается частное решение![]() уравнения (1).
уравнения (1).
Равенство ![]() ,
неявно задающее общее решение уравнения
(1), называется общим интегралом уравнения
(1).
,
неявно задающее общее решение уравнения
(1), называется общим интегралом уравнения
(1).
При решении практических задач приходится искать не общее решение уравнения (1), а его частное решение, удовлетворяющее некоторым определенным условиям. Примером такой задачи является так называемая задача Коши, состоящая в нахождении решения уравнения (1), удовлетворяющего начальным условиям
![]() . (2)
. (2)
При некоторых не очень жестких ограничениях на функцию F задача Коши (1), (2) имеет единственное решение.
2. Уравнение с разделяющимися переменными
Уравнение
вида
![]() называется уравнением с разделяющимися
переменными. Для решения такого уравнения
достаточно
представить
называется уравнением с разделяющимися
переменными. Для решения такого уравнения
достаточно
представить
![]() в виде отношения дифференциалов
в виде отношения дифференциалов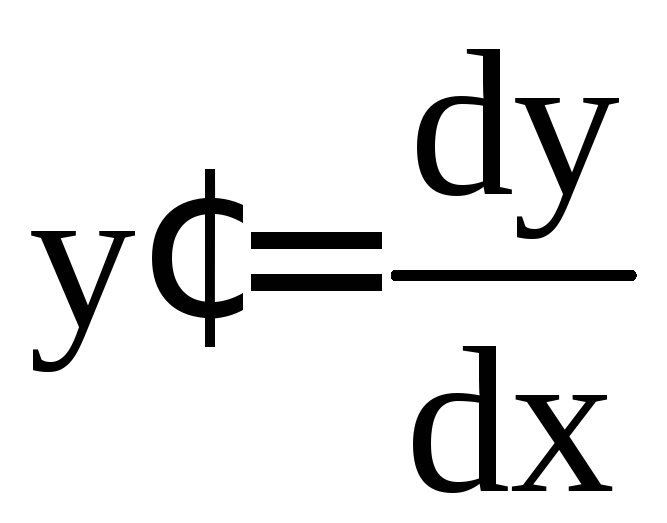 ,
разделить переменные и проинтегрировать
обе части уравнения:
,
разделить переменные и проинтегрировать
обе части уравнения:
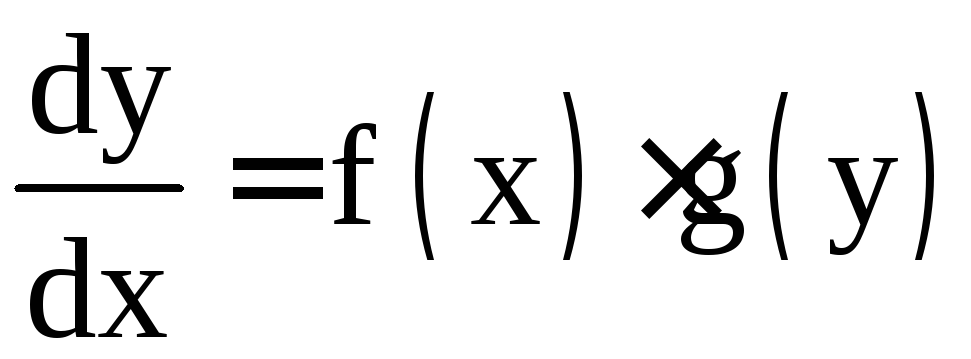 ;
; 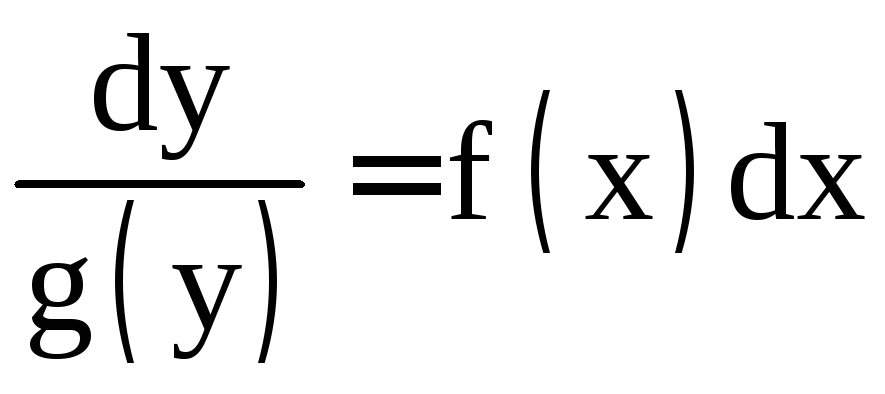 ;
;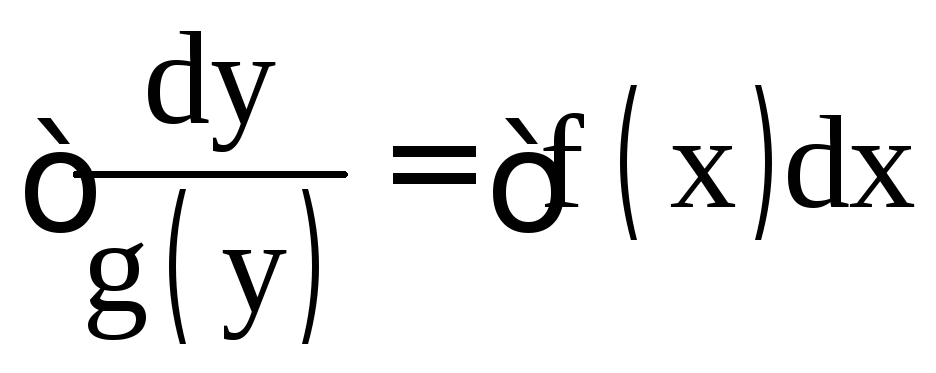 .
.
Пример
1. Решить
уравнение
![]() .
.
Решение.
Имеем:
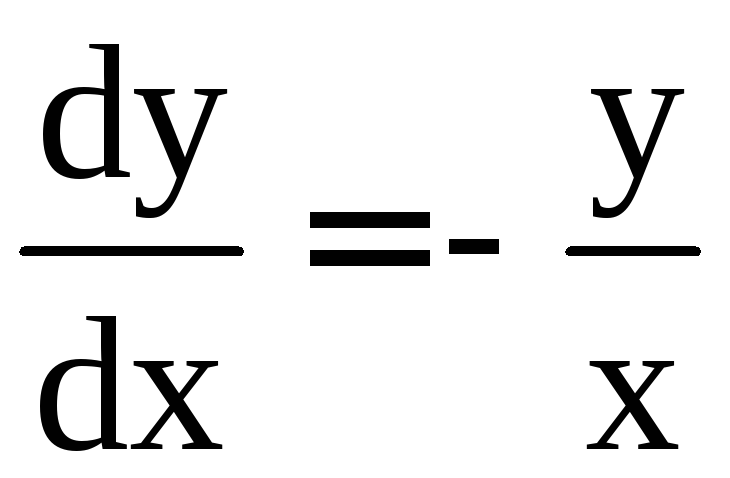 .
.
Разделяя переменные, получим
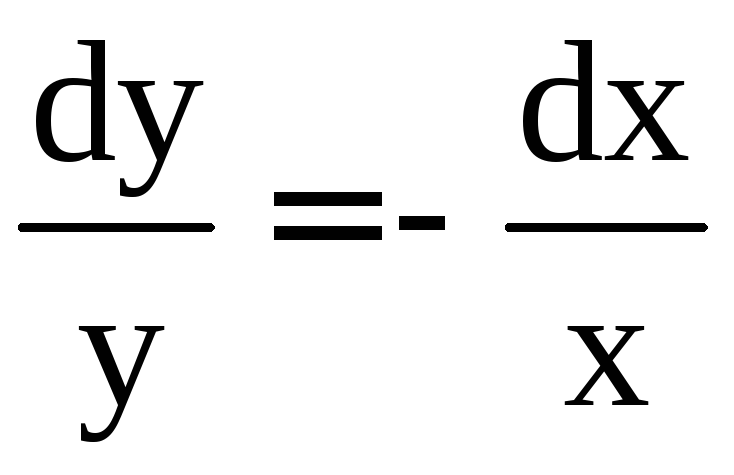 ;
; 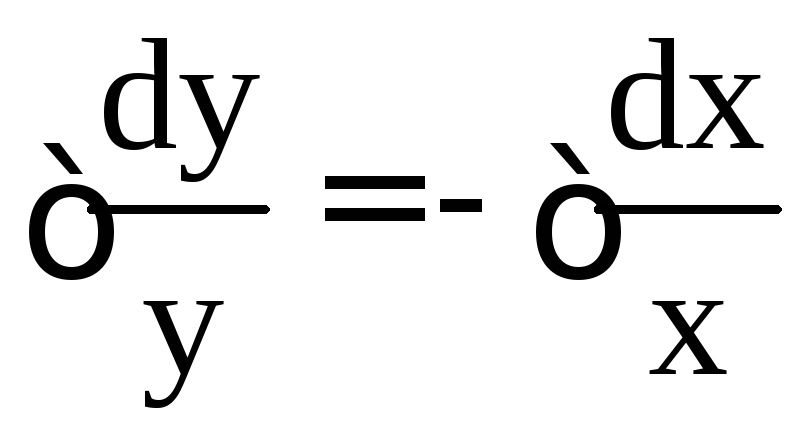 ;
;![]()
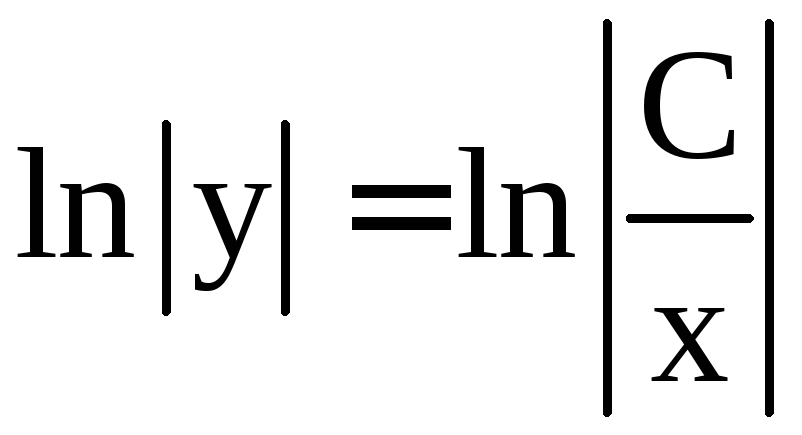 ;
;
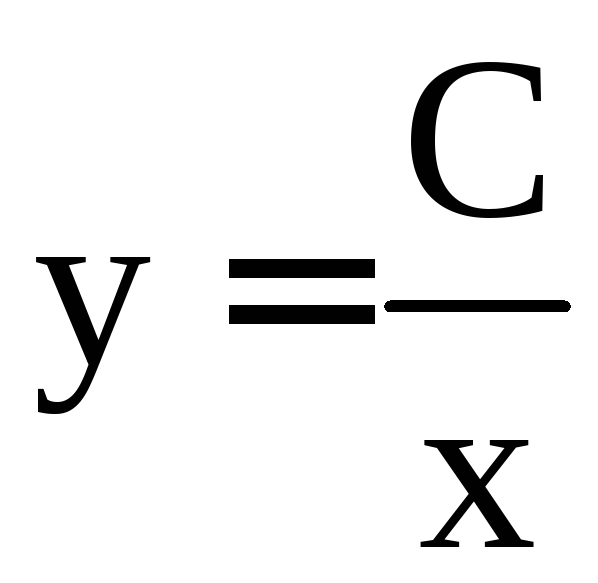 –это
и есть общее решение нашего уравнения.
(Мы положили
–это
и есть общее решение нашего уравнения.
(Мы положили
![]() ;
равенство
;
равенство можно заменить на
можно заменить на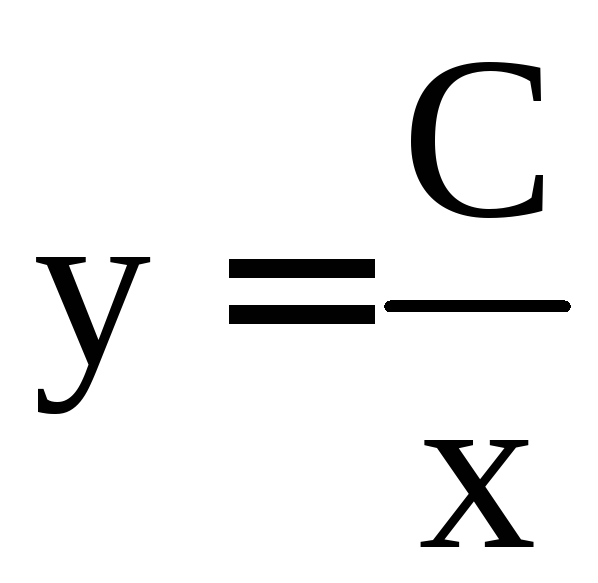 ,
так как неопределенность знака поглощается
константойC.)
,
так как неопределенность знака поглощается
константойC.)
Уравнения с разделяющимися переменными часто пишут в другой форме:
![]() .
.
Пример 2. Решить задачу Коши
![]() ,
, 
Решение. Разделим переменные в уравнении:
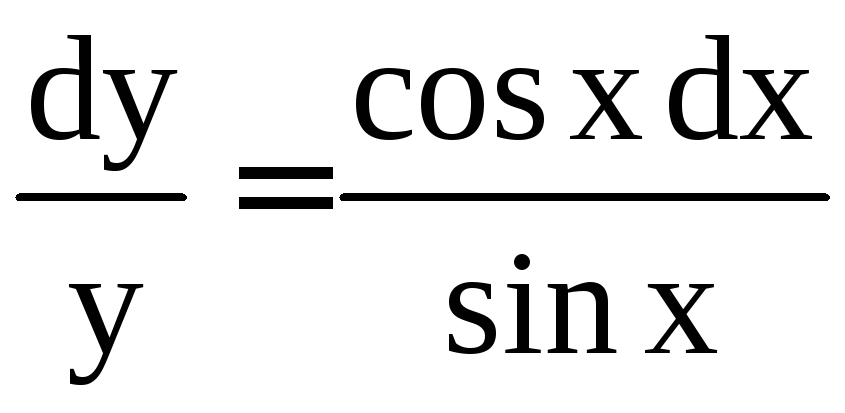 ;
; 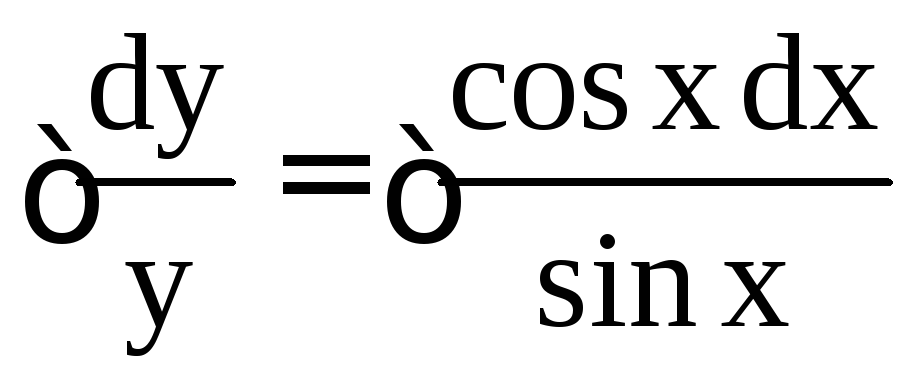 ;
;
![]()
![]() .
.
Отсюда
находим общее решение
![]() .
Для определения константыC
воспользуемся начальным условием
.
Для определения константыC
воспользуемся начальным условием
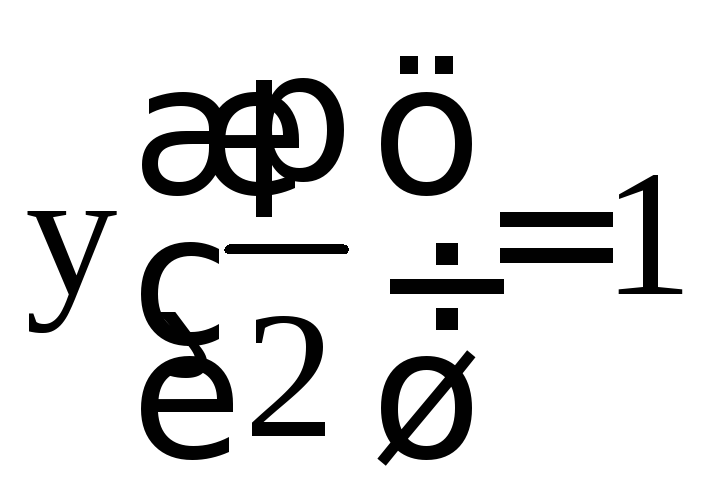 :
:
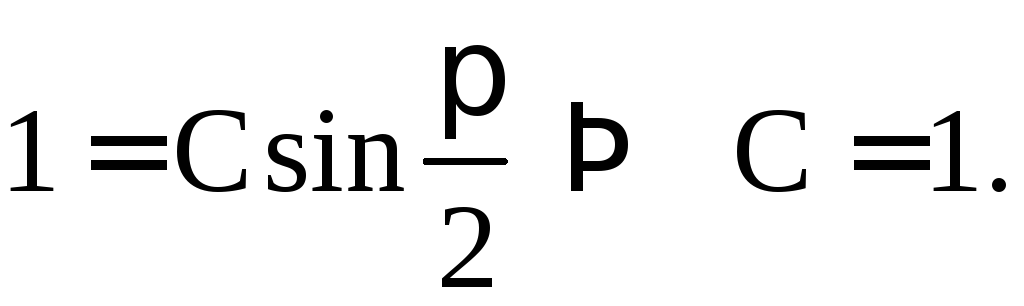 Таким
образом, решением задачи Коши является
Таким
образом, решением задачи Коши является
![]() .
.
Дифференциальное уравнение вида
![]()
c
помощью подстановки
![]() приводится к уравнению с разделяющимися
переменными.
приводится к уравнению с разделяющимися
переменными.
Пример
3. Решить
уравнение
![]() .
.
Решение.
Введем новую
неизвестную функцию
![]() .
.
Тогда
![]() ,
и наше уравнение примет вид
,
и наше уравнение примет вид
![]() .
.
Это уравнение с разделяющимися переменными:
![]()
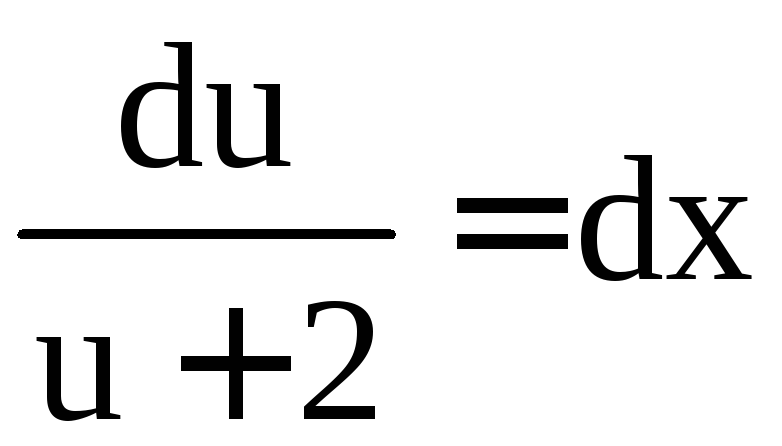 ;
;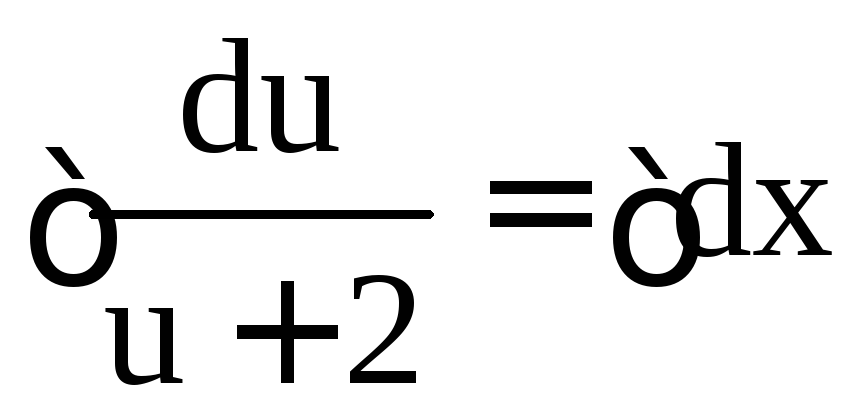 ;
;
![]()
![]() .
.
Отсюда
находим
![]() ;
;![]() – общее решение исходного уравнения.
– общее решение исходного уравнения.
3. Однородные дифференциальные уравнения
Функция
двух переменных называется однородной
функцией n-го
порядка, если
![]() для всех допустимых значений
для всех допустимых значений![]() .
.
Дифференциальное уравнение
![]() (3)
(3)
называется
однородным, если
![]() является однородной функцией нулевого
порядка, т.е. если
является однородной функцией нулевого
порядка, т.е. если![]() .
Однородная функция нулевого порядка
фактически является функцией частного
.
Однородная функция нулевого порядка
фактически является функцией частного![]() :
:
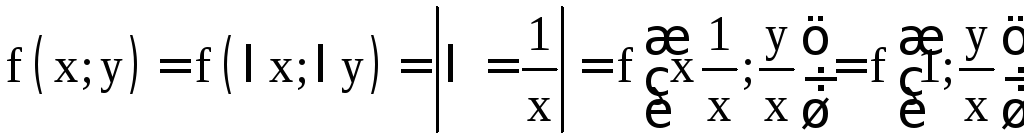 .
.
Поэтому
введением нового переменного (новой
неизвестной функции)
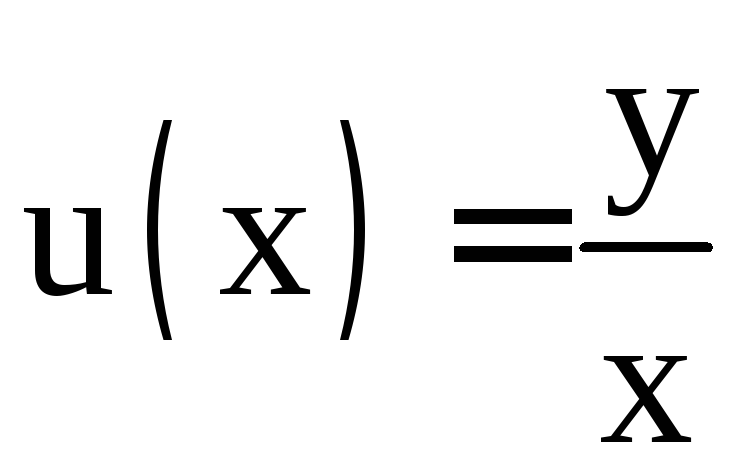 уравнение (3) приводится к уравнению с
разделяющимися переменными:
уравнение (3) приводится к уравнению с
разделяющимися переменными:![]()
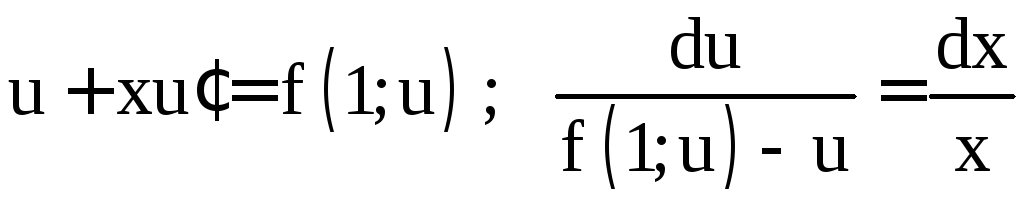 .
.
Пример
4. Решить
уравнение
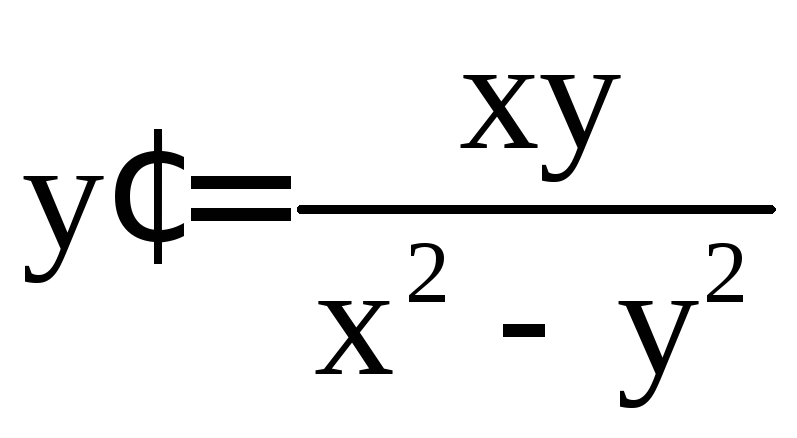 .
.
Решение.
Проверим
функцию
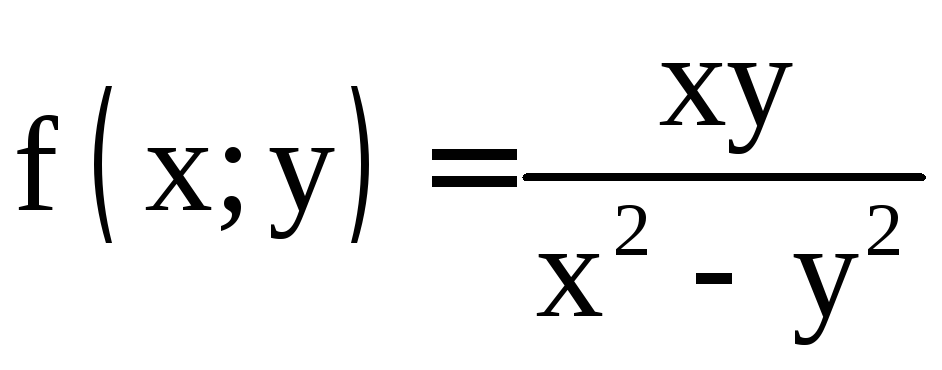 на однородность:
на однородность:
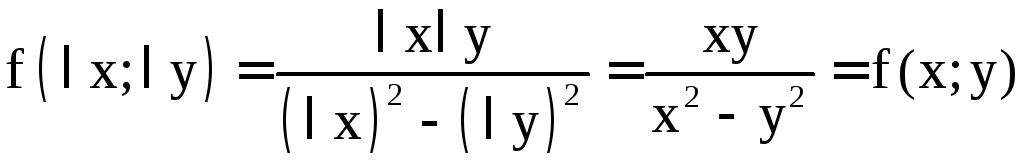 .
.
Следовательно,
наше уравнение является однородным.
Делаем подстановку
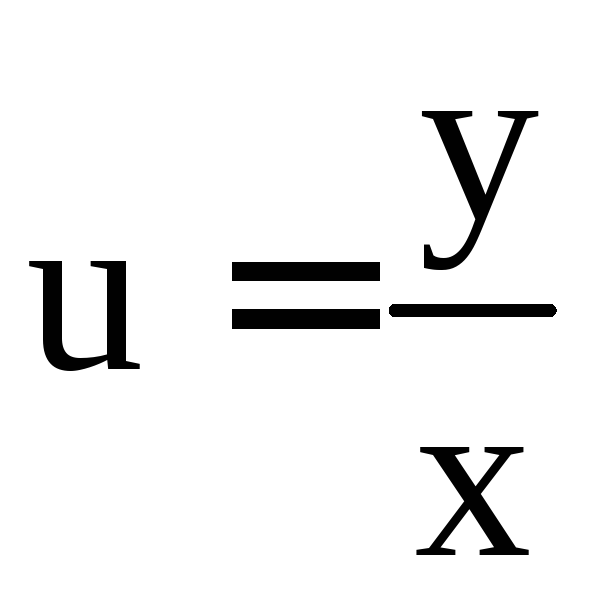 ,
тогда
,
тогда![]() и уравнение принимает вид
и уравнение принимает вид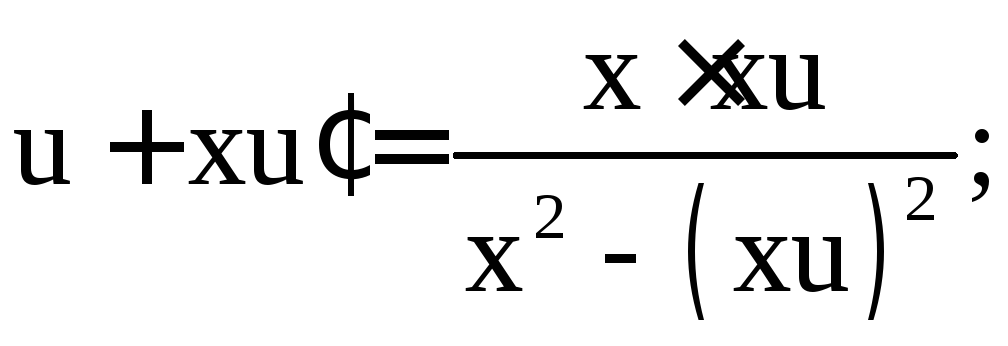
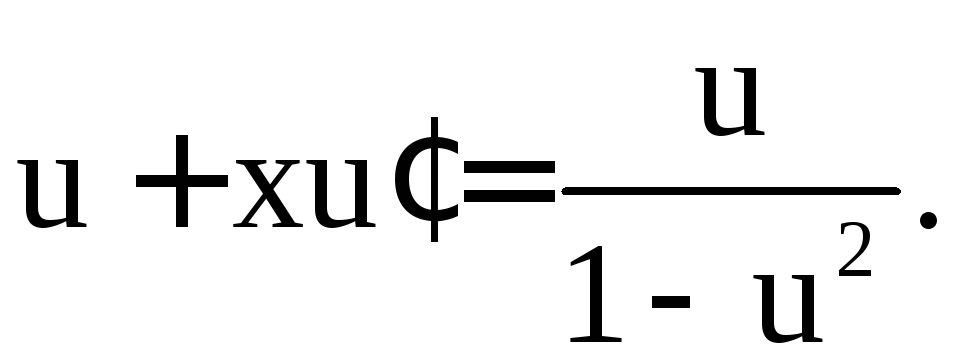
Получим дифференциальное уравнение с разделяющимися переменными:
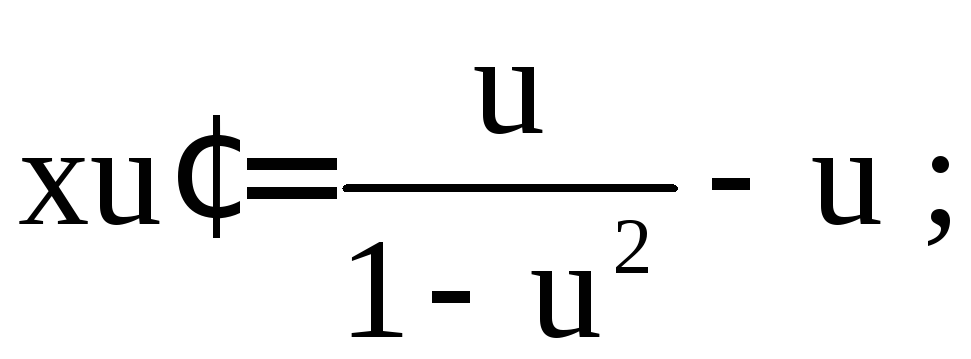
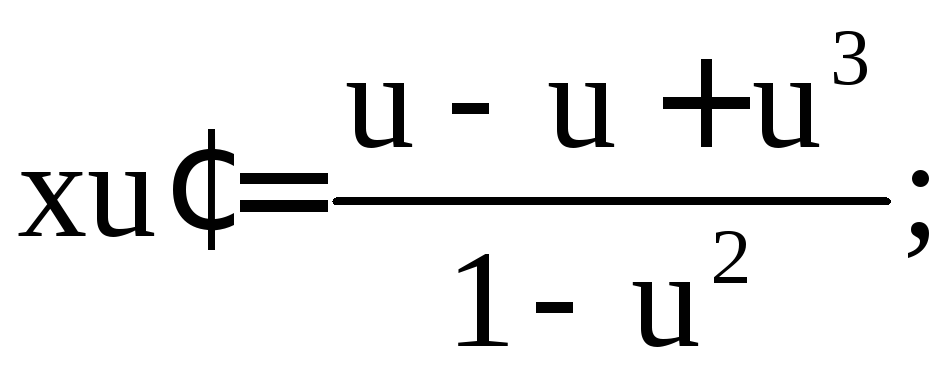
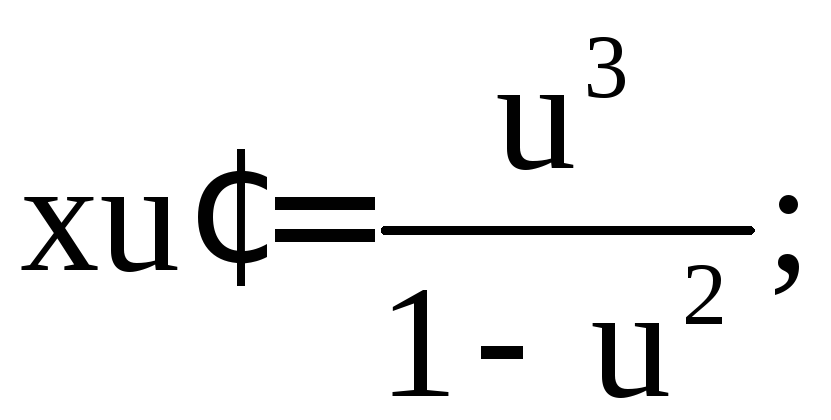
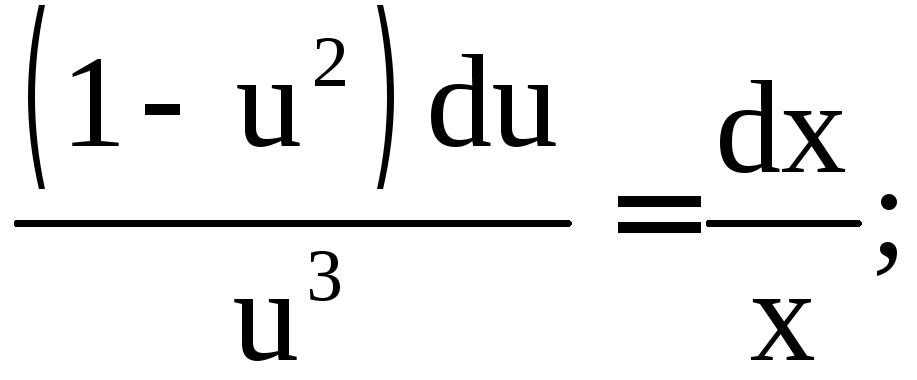

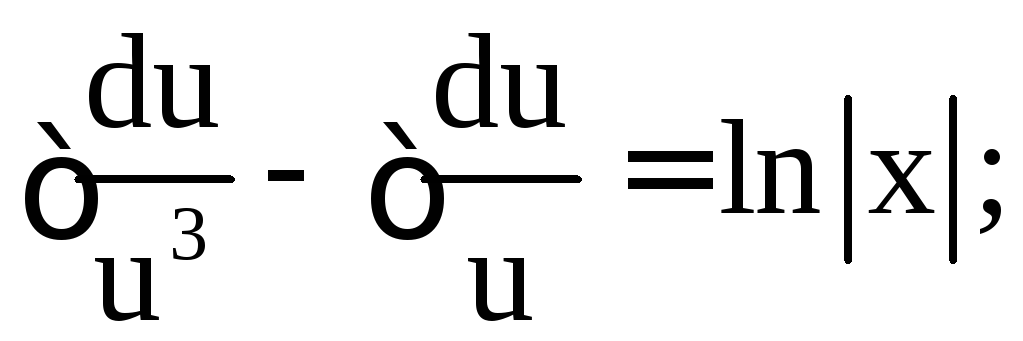


Подставив
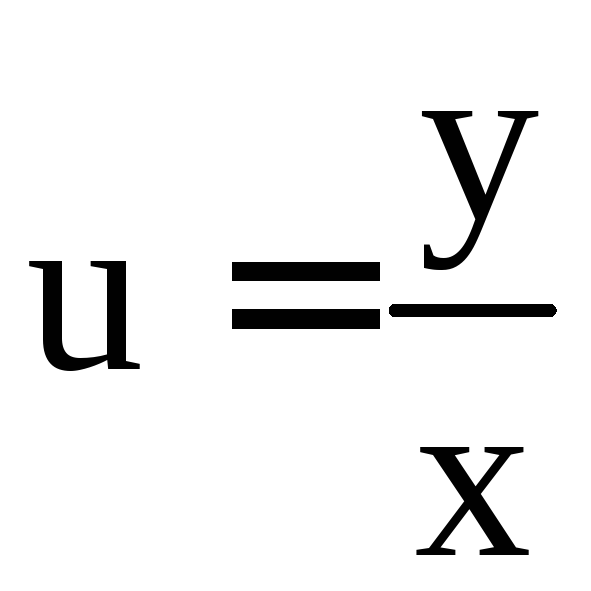 ,
получим
,
получим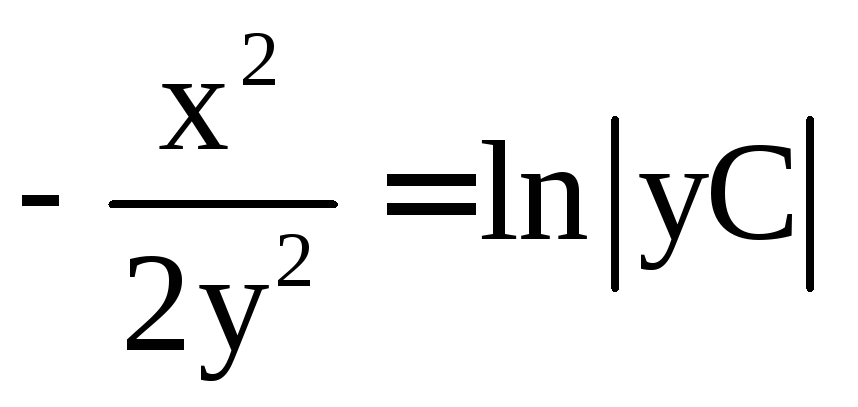 ,
что приводит к общему интегралу исходного
уравнения:
,
что приводит к общему интегралу исходного
уравнения:![]() .
.
Дифференциальное уравнение вида
![]() будет однородным, если
будет однородным, если![]() являются однородными функциями одного
порядка.
являются однородными функциями одного
порядка.
Уравнение
вида 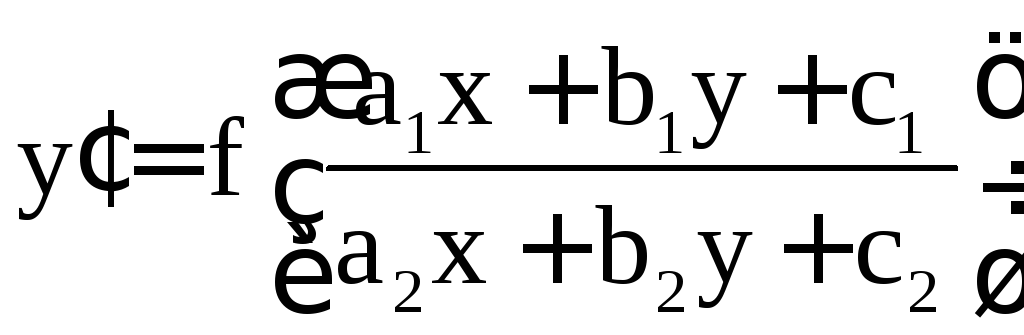 (4)
(4)
в
случае
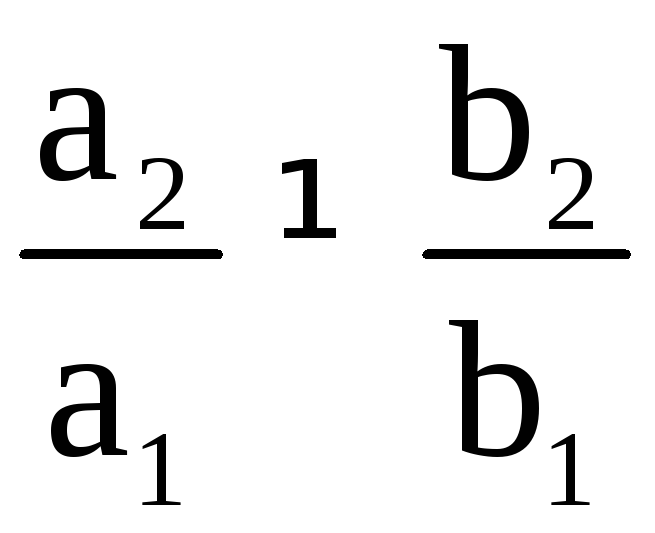 ,
приводится к однородному с помощью
замены переменных
,
приводится к однородному с помощью
замены переменных
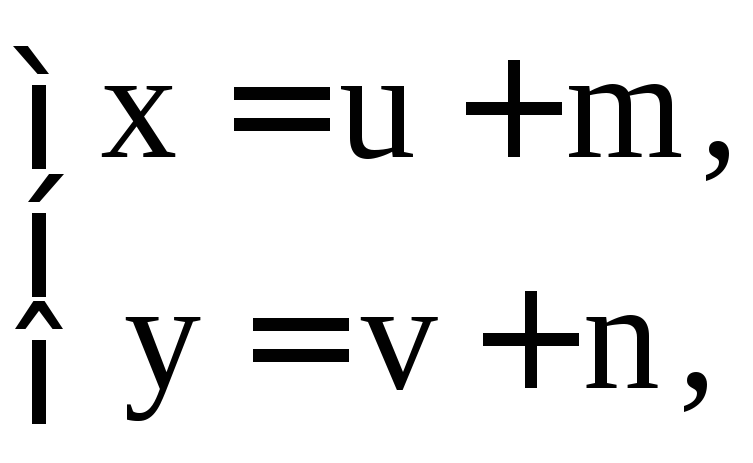
где m и n являются решением системы
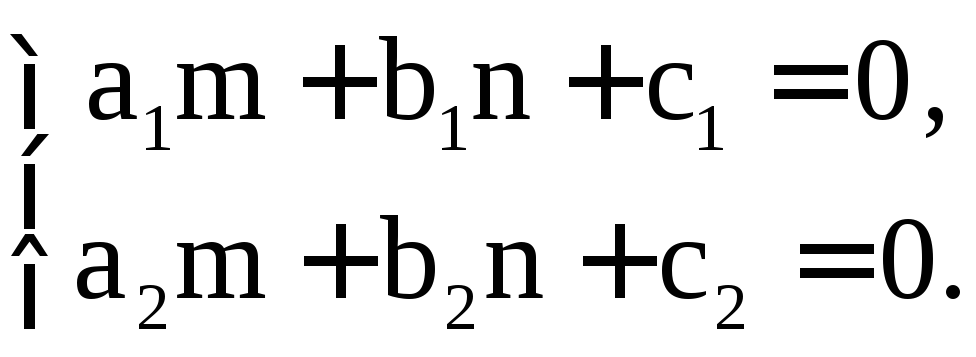
Пример
5. Решить
уравнение
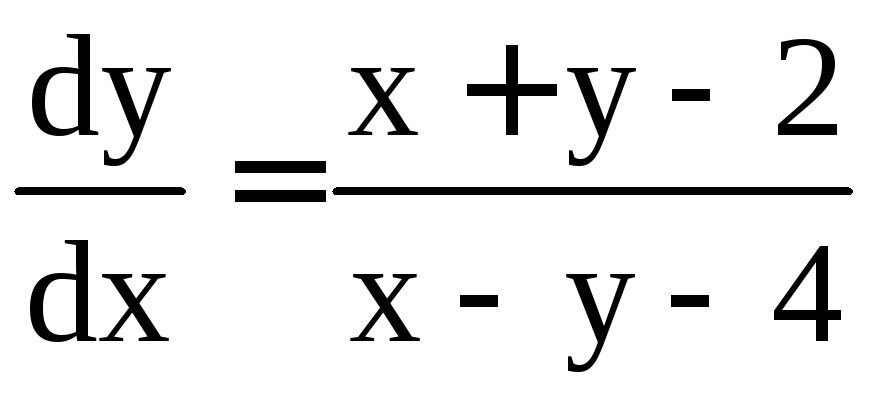 .
.
Решение.
В этом случае
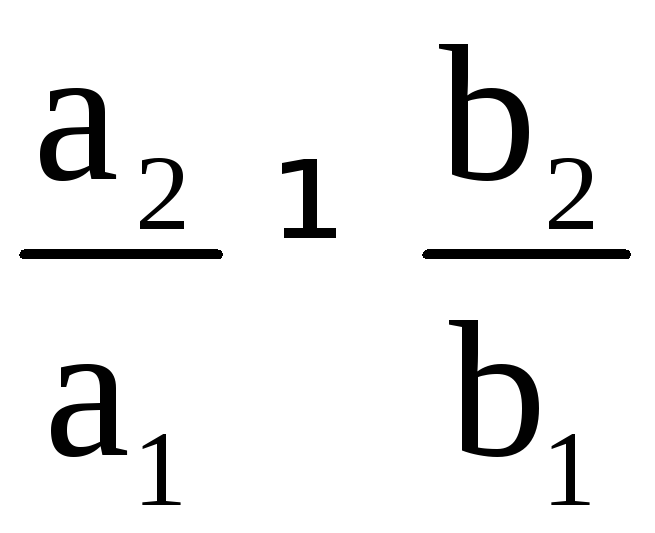 .
Сделаем замену переменных
.
Сделаем замену переменных
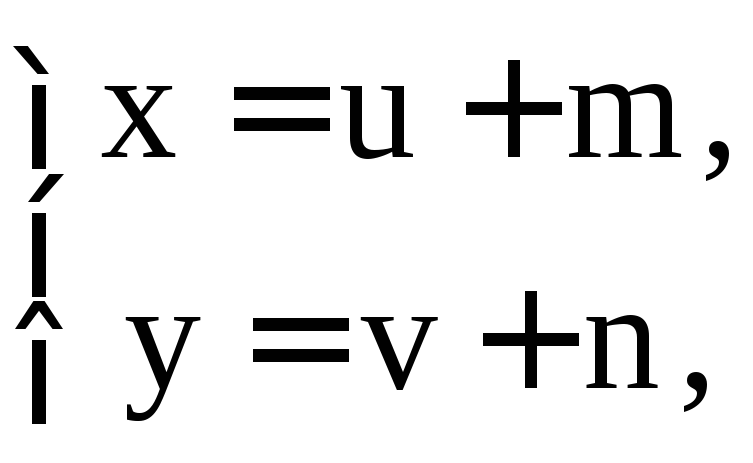
dx =du, dy =dv. Уравнение примет вид
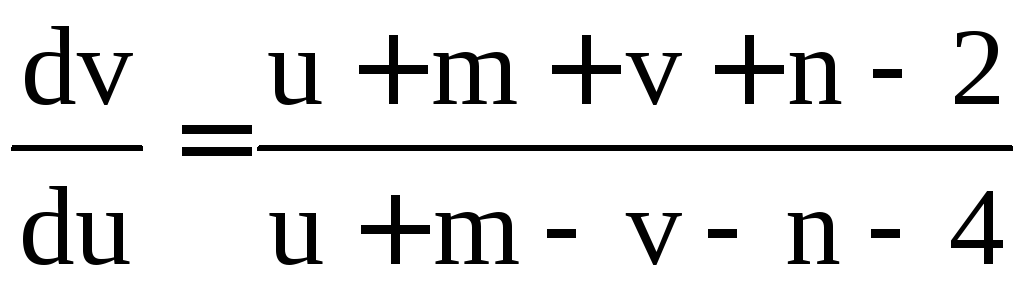 .
.
Подберем m и n так, чтобы выполнялись равенства
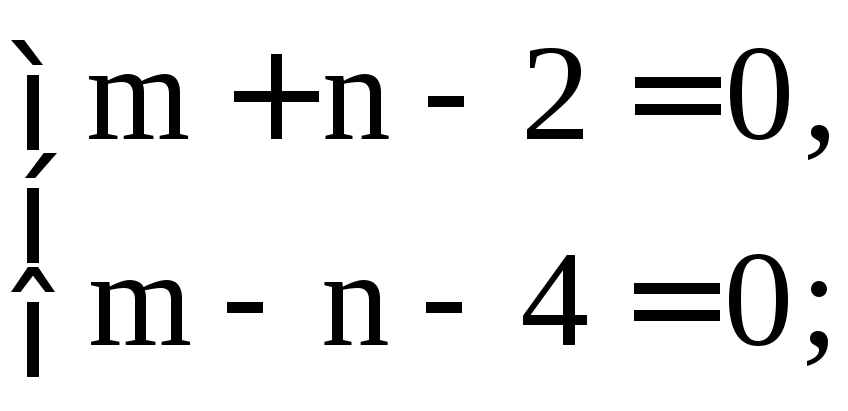 =>
=>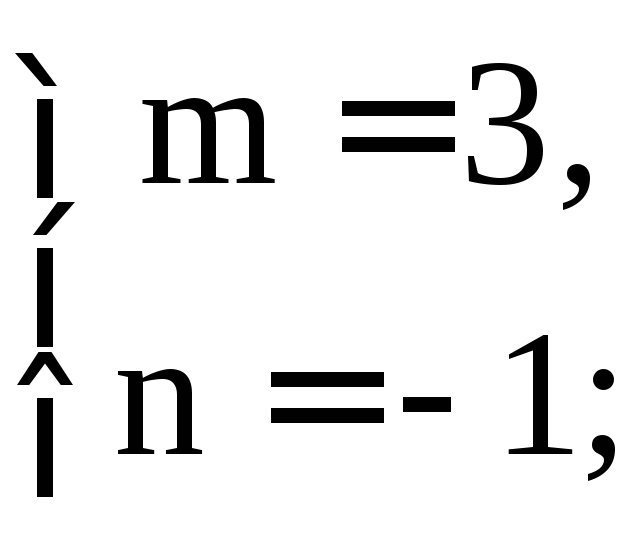
Подставляя эти значения m и n в уравнение, получим
 .
.
Положим
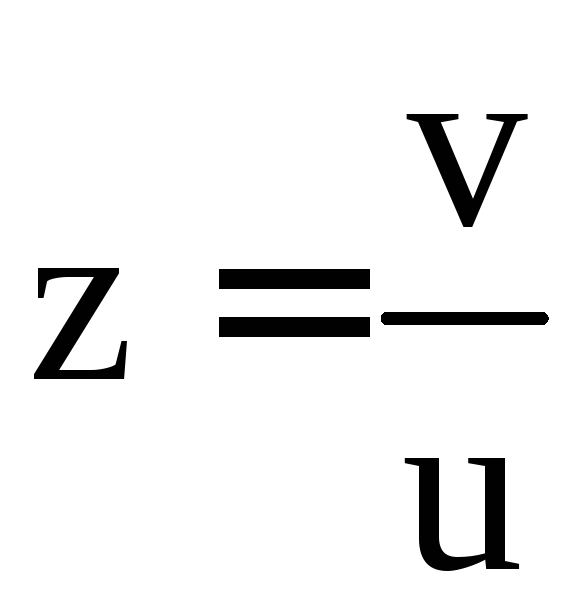 ,
тогда
,
тогда![]() ,
,![]() .
Уравнение примет вид
.
Уравнение примет вид
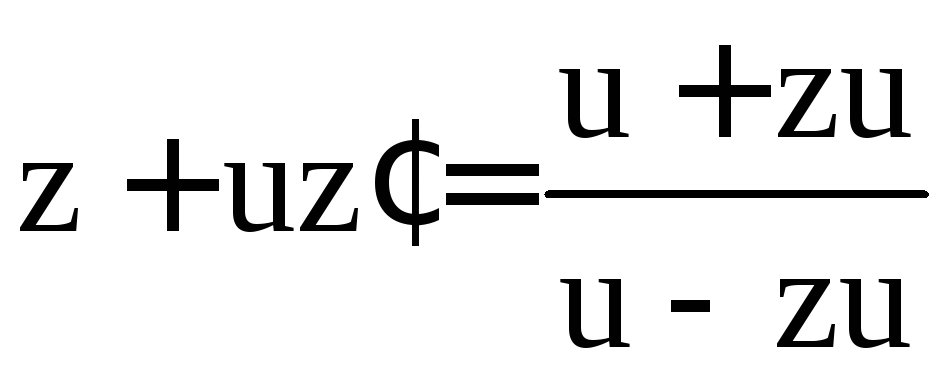 ;
; 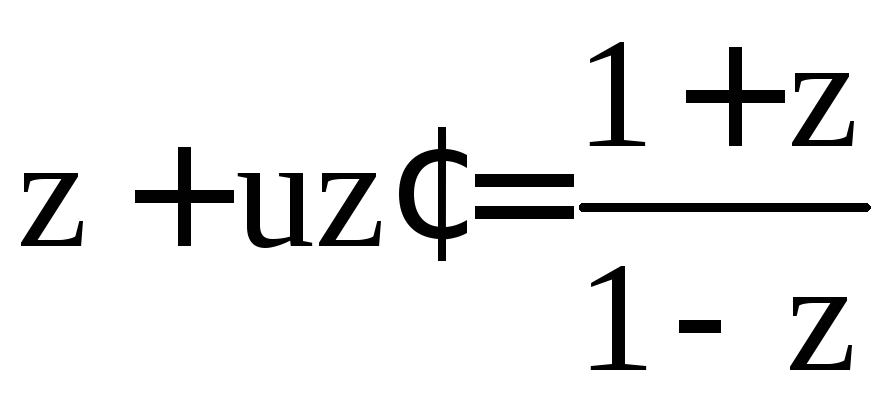 ;
;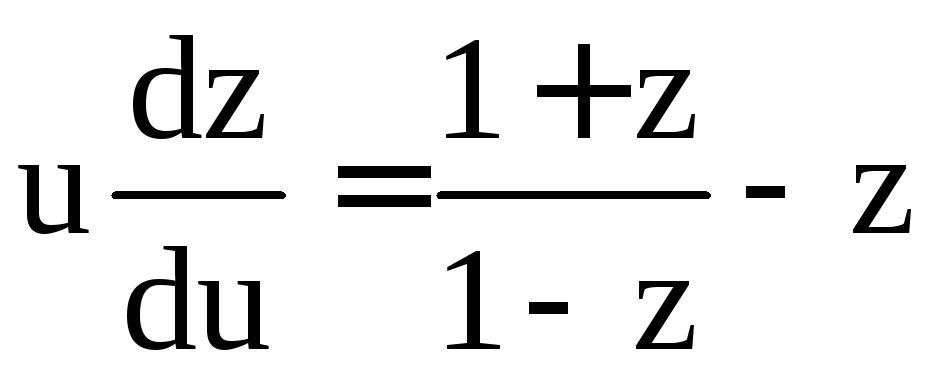 ;
;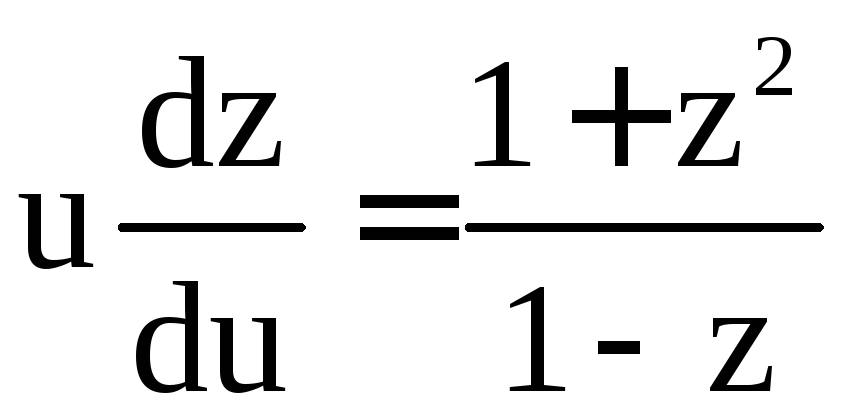 .
.
Разделяя переменные, решим это уравнение:
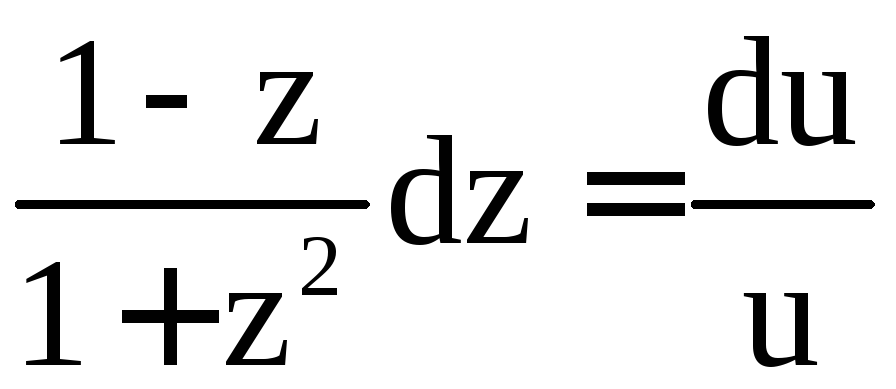 ;
; 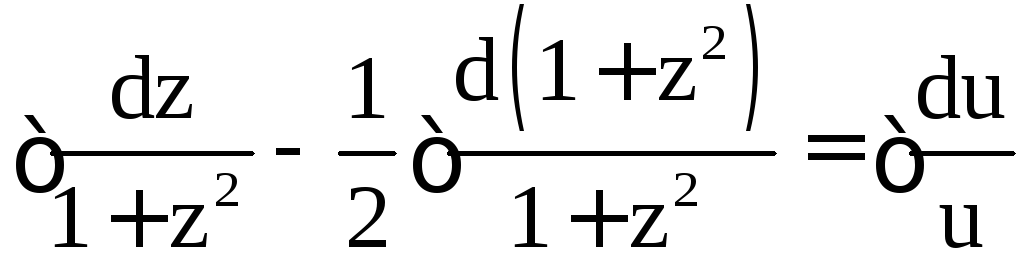 ;
;
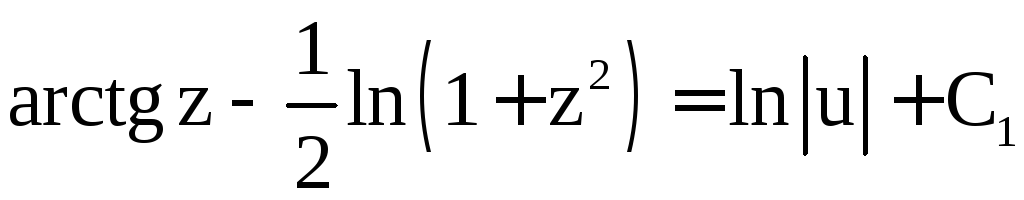 ;
;
![]()
Вспомним,
что
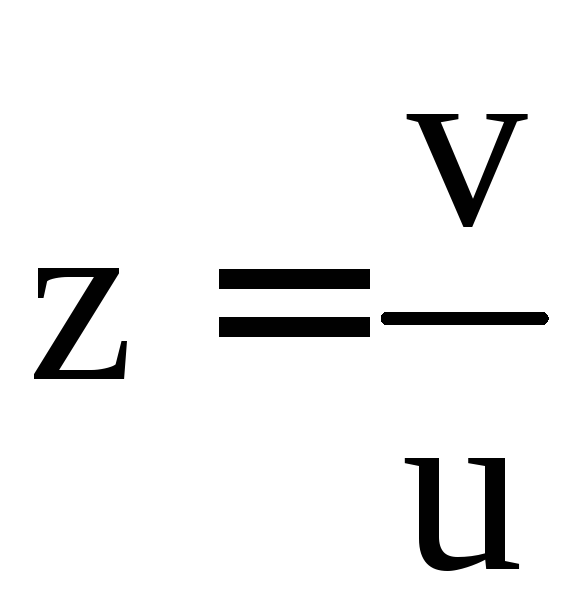 :
:
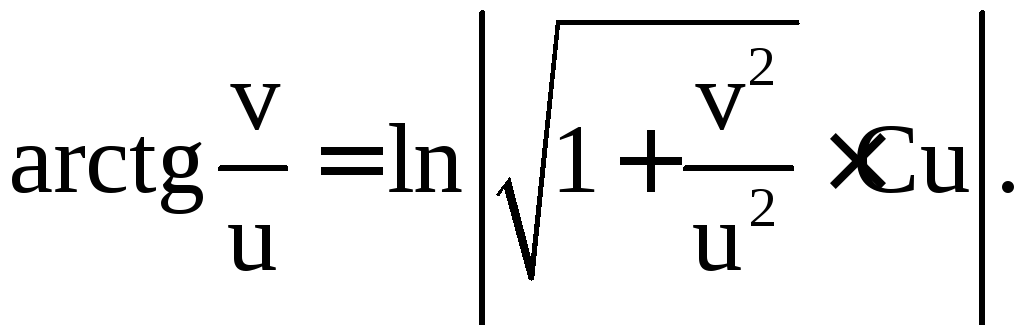
Учтем,
что
![]()
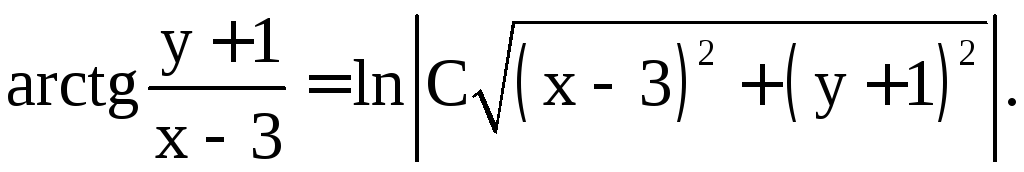
Это и есть общий интеграл исходного уравнения.
Если
в уравнении (4)
 ,
т.е.
,
т.е.![]() ,
то это уравнение принимает вид
,
то это уравнение принимает вид
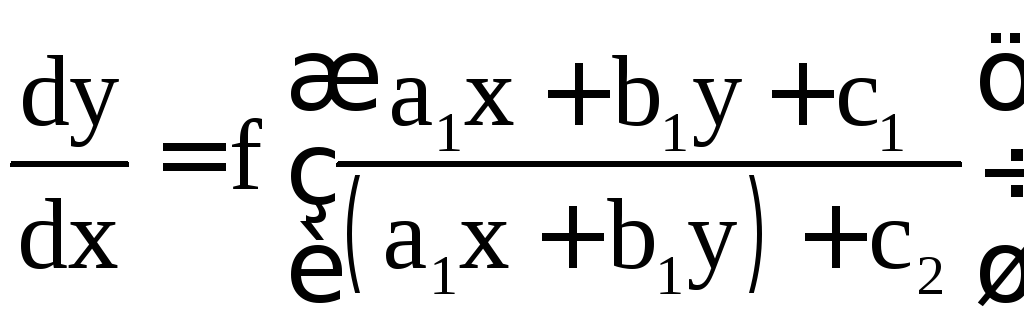 . (5)
. (5)
Подстановкой
![]() последнее уравнение приводится к
уравнению с разделяющимися переменными.
последнее уравнение приводится к
уравнению с разделяющимися переменными.
Пример
6. Решить
уравнение
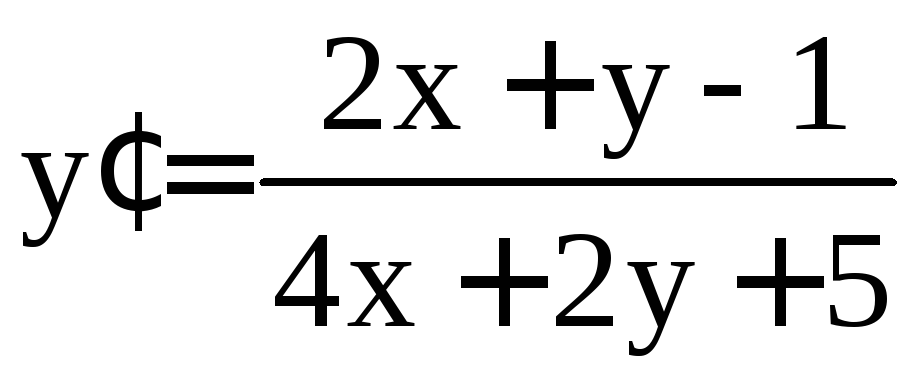 .
.
Решение.
В этом случае
 .
Введем новую неизвестную функцию
.
Введем новую неизвестную функцию![]() .
Тогда
.
Тогда![]()
![]() Наше уравнение примет вид
Наше уравнение примет вид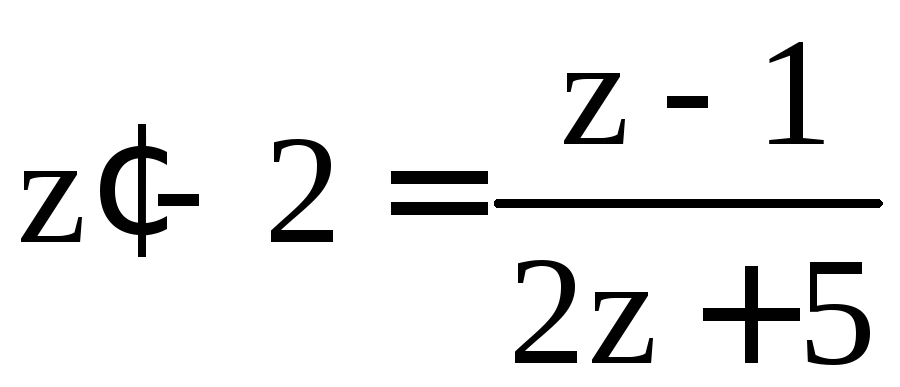 ;
;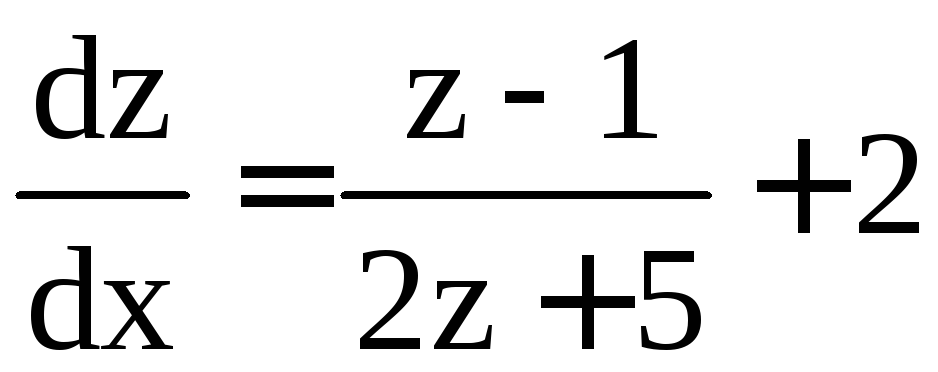 ;
;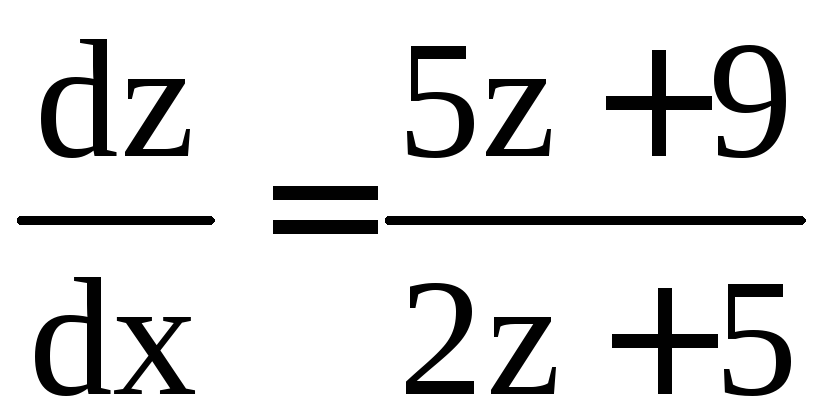 ;
;
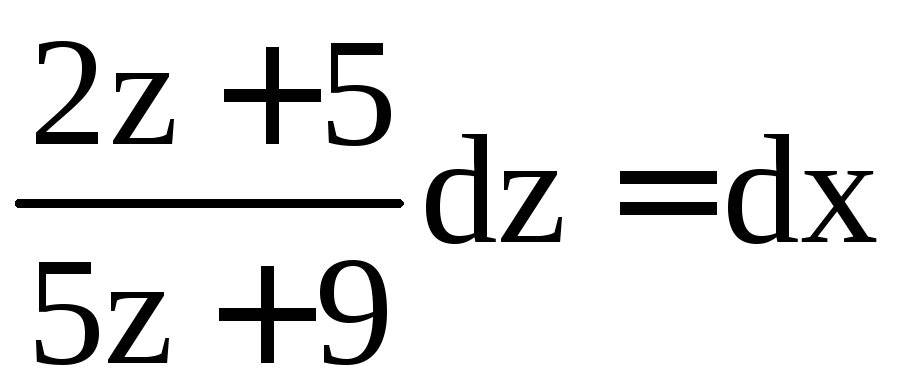 ;
; 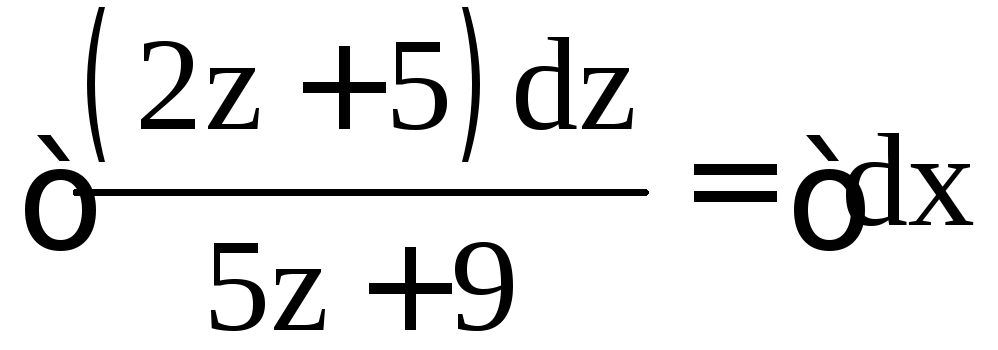 ;
;
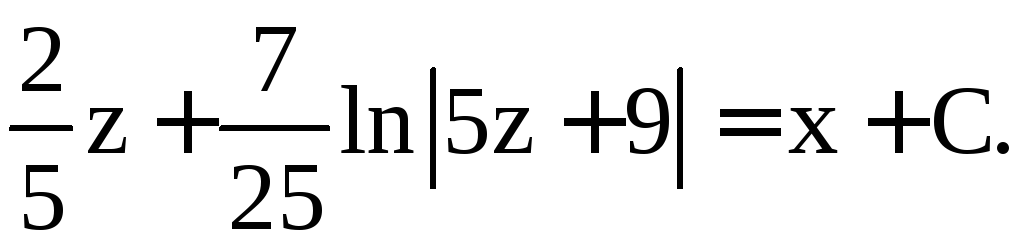
Подставив
![]() ,
получим
,
получим
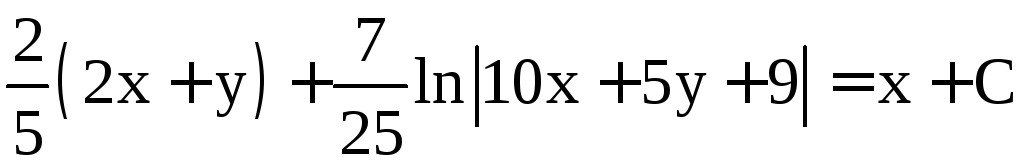 .
.
Это и есть общий интеграл нашего уравнения.
