14. Линейные неоднородные системы дифференциальных уравнений

Рассмотрим линейную неоднородную систему дифференциальных уравнений

(23)

Здесь – известныe функции, – искомые функции.

Система (23) может быть записана в матричной форме

,

где .

Если – общее решение линейной однородной системы дифференциальных уравнений

(22)

соответствующей неоднородной системе (23) (т.е. имеющей те же коэффициенты ), и– некоторое частное решение неоднородной системы (23), то согласно теореме 5 общее решение неоднородной системы (23) имеет вид

(27)

Другими словами, если – ФСР однородной системы (22), а– некоторое частное решение неоднородной системы (23), то общим решением системы (23) будетгде–произвольные постоянные.

Если известна фундаментальная система решений однородной системы (22), то общее решение неоднородной системы (23) может быть найдено методом вариации постоянных. Это означает, что общее решение системы (23) ищется в виде

где – неизвестные функции. Подстановка такой вектор-функции X(t) в (23) приводит к системе

Решив эту систему относительно функций , найдем

.

В случае, если в системе (23) функции являются постоянными величинами, а функцииимеют вид, где– многочлены степени меньше либо равныеk, и – корень кратностью r характеристического уравнения,, то частное решение системы (23) следует искать в виде

,

где  k – наибольшая степень многочленов . Если жене является корнем характеристического уравнения, т.е., то частное решениеищется в виде

.

Если – частное решение системы

–частное решение системы

то вектор-функция является частным решением системы

Аналогичное утверждение справедливо и для большего числа слагаемых.

Пример 27. Решить систему

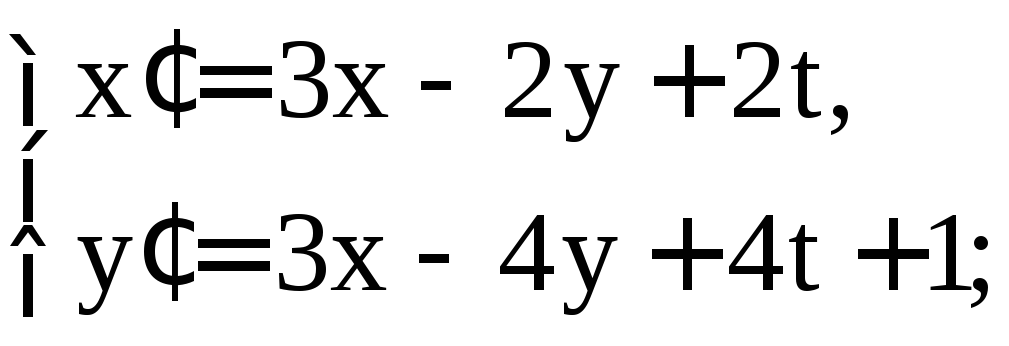(28)

а) методом вариации постоянных;

б) методом подбора специального частного решения.

Решение. а) Найдем общее решение однородной системы

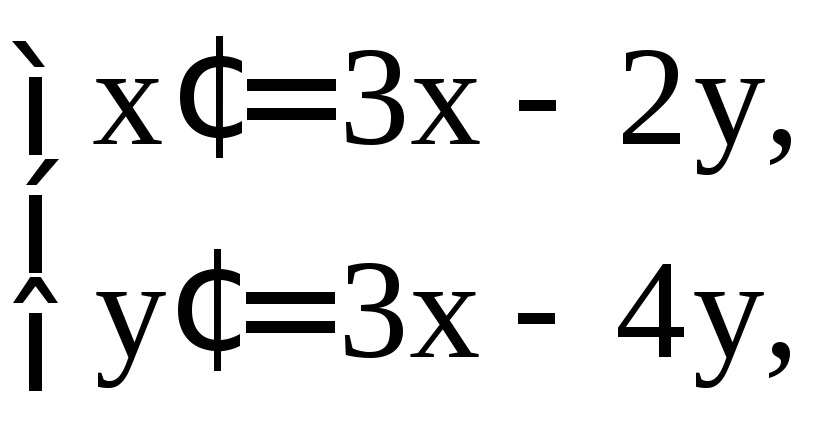
Соответствующие однородное СЛАУ и характеристическое уравнение имеют вид:

()

;

Найдем собственные векторы, отвечающие собственным значениям

Подставляя в СЛАУ (), получаем систему алгебраических уравнений

которая равносильна уравнению . В качестве собственного вектора можно взять. Ему соответствует вектор-функция

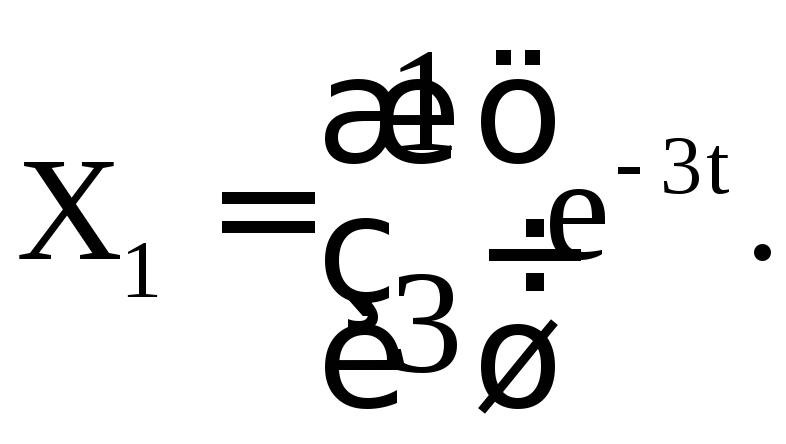
приводит к системе

которая равносильна уравнению . В качестве собственного вектора возьмем, которому отвечает вектор-функция

Вектор-функции образуют фундаментальную систему решений однородной системы дифференциальных уравнений, поэтому общее решение этой однородной системы имеет вид

или

Будем искать решение нашей неоднородной системы дифференциальных уравнений в виде

(29)

Подставляя (29) в (28) приходим к системе уравнений относительно и

Решим эту линейную относительно исистему методом Крамера

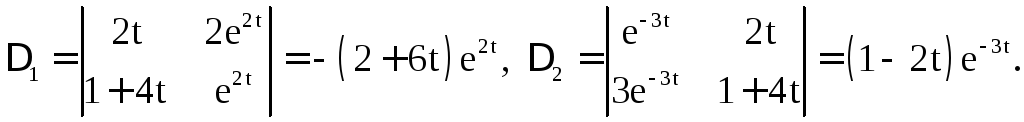
Отсюда находим

Интегрированием этих функций найдем и:

Значит, общим решением неоднородной системы является

;

или

б) Как мы видели выше, общее решение соответствующей однородной системы имеет вид

Найдем частное решение неоднородной системы. В нашем случае

Число не является корнем характеристического уравнения

,

поэтому ищем в виде

т.е. .

Имеем

Подставим x(t), y(t) в нашу неоднородную систему, получим систему

Приравняв коэффициенты при соответствующих степенях t, приходим к системе

Таким образом,

и общим решением неоднородной системы является

или

Пример 28.  Решить      неоднородную     систему     линейных дифференциальных уравнений с постоянными коэффициентами

Решение. Путем исключения одной из неизвестных функций систему можно свести к уравнению второго порядка с одной неизвестной функцией.

Например, путем исключения функции систему сведем к уравнению второго порядка относительно функции.

Найдем из 1-го уравнения системы:. Отсюда имеем. Подставив значенияиво второе уравнение системы, получим неоднородное линейное дифференциальное уравнение второго порядка относительно неизвестной функции:

Найдем его общее решение по формуле , где- общее решение однородного уравнения, а-некоторое частное решение неоднородного уравнения.

Характеристическое уравнение соответствующего однородного дифференциального уравнения имеет коренькратностью    2, следовательно, общее решение однородного дифференциального уравнения имеет вид

.

Частное решение неоднородного дифференциального уравнения найдем методом неопределенных коэффициентов.

Правая часть неоднородного дифференциального уравнения имеет вид

Поэтому

Найдем и:

Подставив в заданное неоднородное дифференциальное уравнение, приведем подобные члены

Сравнивая коэффициенты при иполучим СЛАУ для определения неизвестных

Итак,

Следовательно, общее решение имеет вид

Функцию определим, воспользовавшись соотношением

Таким образом, общее решение данной системы дифференциальных уравнений имеет вид