4. Линейные дифференциальные уравнения первого порядка
Линейное дифференциальное уравнение первого порядка имеет вид
. (6)
Для решения уравнения (6) пользуются двумя методами: вариации постоянной и методом подстановки.
А. Метод вариации постоянной. Рассмотрим сначала линейное однородное уравнение (при котором правая часть равна нулю)
. (7)
Это уравнение с разделяющимися переменными; его общим решением является
.
Будем
искать решение уравнения (6) в виде
,
где
–
неизвестная функция. Имеем
.
Подставляя
в уравнение (6), получим
,
или
.
Последнее
уравнение является уравнением с
разделяющимися переменными, в котором
неизвестной функцией выступает
:
; 
.
Таким образом, решением уравнения (6) является
.
Б. Метод
подстановки. Будем
искать решение уравнения (6) в виде
.
Тогда
и уравнение (6) примет вид
,
или
. (8)
Потребуем, чтобы выражение в скобках было равно нулю:
Это
уравнение с разделяющимися переменными;
найдем некоторое частное решение
этого уравнения:
; 
.
Подставим
в формулу (8):
Это
дифференциальное уравнение также
является уравнением с разделяющимися
переменными. Пусть
– общее решение последнего уравнения.
Тогда общим решением уравнения (6)
является
.
Пример
7. Решить
уравнение
.
Решение. А. Метод
вариации постоянной.
Решим сначала соответствующее однородное
уравнение
.
Это уравнение с разделяющимися
переменными:
;
–общее
решение однородного уравнения. Общее
решение неоднородного уравнения будем
искать в виде
,
где
– неизвестная функция. Имеем
.
Исходное уравнение примет вид
;
; 
;
.
Таким образом, общим решением исходного уравнения является
.
Б.
Метод подстановки. Будем
искать решение линейного уравнения
в виде
.
Тогда
и уравнение принимает вид
,
или
. (*)
Потребуем, чтобы выражение в скобках было равно нулю:
;
решим это уравнение с разделяющимися
переменными:
; 
;
;
; 
.
Положив
,
найдем частное решение этого уравнения:
.
Подставим
в (*) (при этом первое слагаемое обратится
в 0):
;
; 
.
Итак, общим решением исходного уравнения является
.
5. Уравнение Бернулли
Уравнением
Бернулли называется дифференциальное
уравнение вида
где
.
Как
и линейное уравнение, уравнение Бернулли
можно решить с помощью подстановки
.
Пример
8. Решить
уравнение
.
Решение.
Будем искать решение этого уравнения
в виде
.
Имеем
;
уравнение примет вид
;
. (**)
Выберем
так, чтобы
:
; 
;
.
Положив
,
получаем частное решение
.
Подставим
в уравнение (**):
;
;
.
Решим это уравнение с разделяющимися переменными:
; 
;
;
.
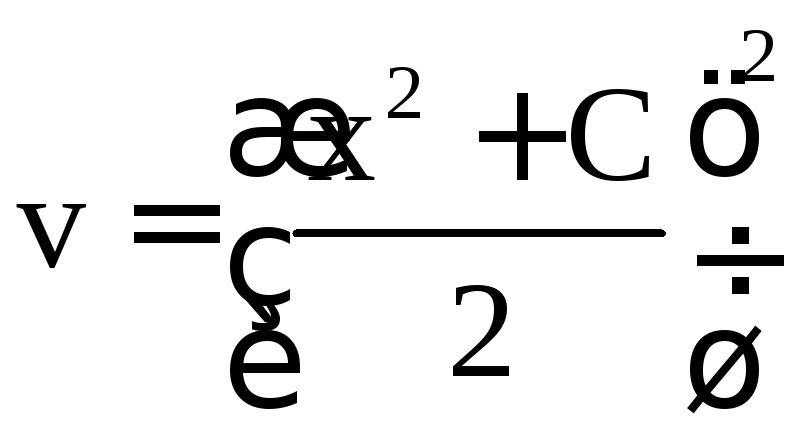Таким образом, общим решением исходного уравнения является
.
6. Уравнение в полных дифференциалах
Дифференциальное уравнение вида
(9)
называется
уравнением
в полных дифференциалах,
если существует такая дифференцируемая
функция
,
что
Общим
интегралом уравнения (9) является
.
Для того чтобы уравнение (9) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось условие
во всех допустимых точках.
Функцию
можно
найти из равенства
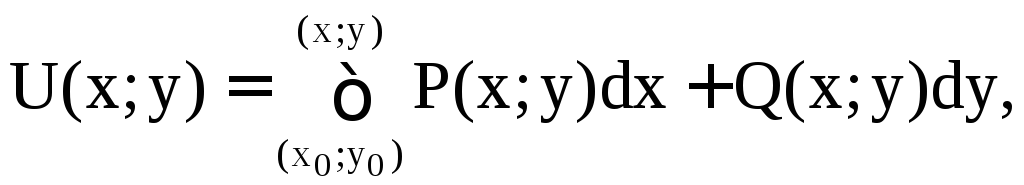
или
.
Пример
9. Решить
уравнение
.
Решение.
Здесь
Так
как
,
то это уравнение в полных дифференциалах.
Найдем функцию
Таким образом, общим интегралом исходного уравнения является
