VIII. Дифференциальное исчисление функций многих переменных

1. Арифметическое пространство. Функции многих переменных

Арифметическим n-мерным пространством A_n называется совокупность всевозможных упорядоченных наборов действительных чисел (x₁; x₂; ...; x_n), называемых точками A_n. В A_n вводится расстояние между точками и

по формуле

.

n-мерным открытым (замкнутым) шаром радиуса r с центром в точке называется множество точек, координаты которых удовлетворяют неравенству

.

Открытый шар радиусом  с центром в точке называется-окрестностью точки M.

Множество (D)  A_n называется открытым, если оно наряду с каждой своей точкой содержит и некоторую её -окрестность. Точка называется граничной точкой множества (D), если любая -окрестность точки M содержит как точки, принадлежащие (D), так и точки, не принадлежащие (D); граничная точка может принадлежать, может и не принадлежать множеству (D). Совокупность всех граничных точек множества (D) образует границу множества (D). Множество, содержащее в себе свою границу, называется замкнутым.

Множество (D)  A_n называется ограниченным, если его можно заключить в некоторый n-мерный шар конечного радиуса.

Множество (D)  A_n называется связным, если любые две его точки можно соединить непрерывной линией, целиком лежащей в (D).

Открытое связное множество в A_n называется открытой областью (или просто областью). Область вместе со своей границей образует замкнутую область.

Пусть (D) – некоторое множество в A_n. Если задано правило f, согласно которому каждой точке ставится в соответствие вполне определённое число, то говорят, что на множестве (D) задана функцияот переменныхМножество (D) называется множеством определения функции f, а множествосуществует M (D), такое что называется множеством значений этой функции. Множество точекпространстваA_n+1 называется графиком функции . В случае функции двух переменныхграфик функции (при некоторых ограничениях на f) оказывается поверхностью в пространствеR₃.

Пример 1. Найти область определения функции . Найти.

Решение. Областью определения функции является решение неравенства или. Последнее неравенство определяет круг радиусом 2 с центром в точке 0(0; 0)..

2. Предел и непрерывность функции

Число A называется пределом функции при стремлении точкик точке, если для любогосуществует такое, что неравенствовлечет неравенство.

При этом пишут или.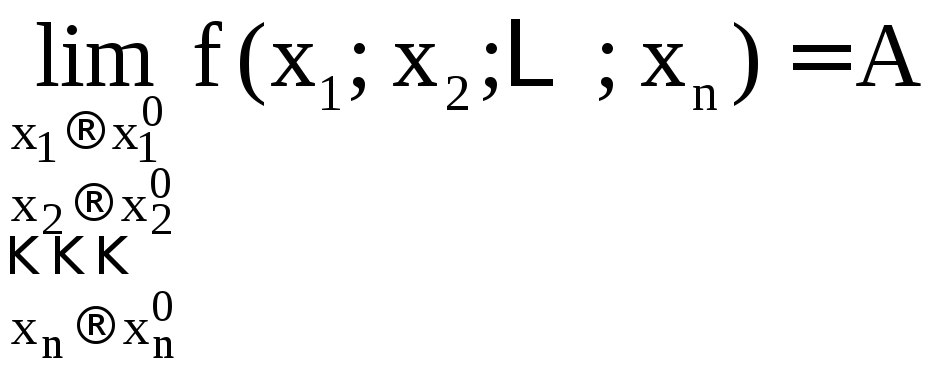

Предел функции многих переменных обладает практически теми же свойствами, что и предел функции от одного переменного (предел суммы равен сумме пределов и т. п.).

Пример 2. Найти предел .

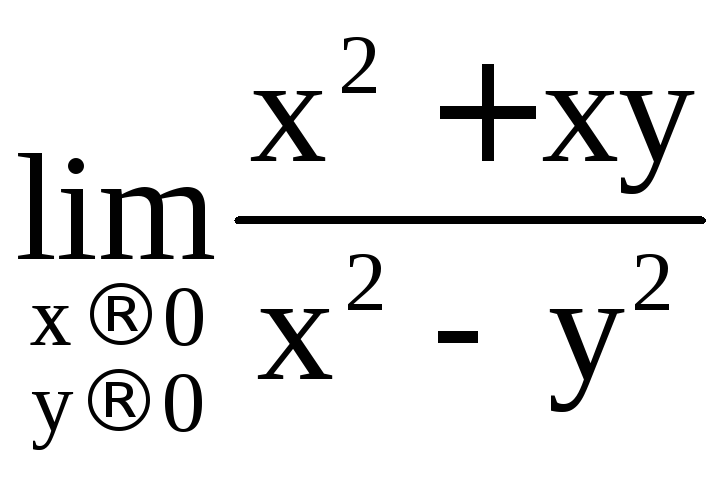Решение. Пусть точка N(x; y) стремится к точке 0(0; 0) вдоль прямой y = kx, x  0. Тогда

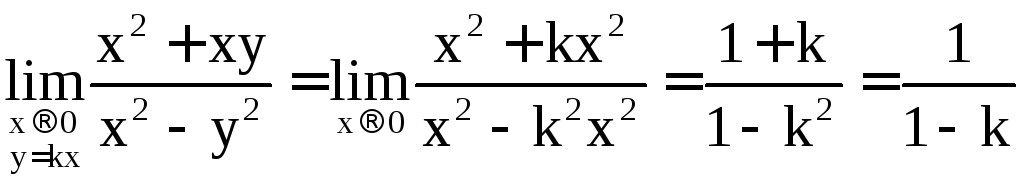, k  1.

Видим, что предел зависит от коэффициента k. Следовательно, наша функция не имеет предела при .

Функция , определённая в некоторой окрестности точки, называется непрерывной в этой точке, если. В противном случае (т.е. f(M) не определена или не существует конечного предела) точка M называется точкой разрыва функции. Функция, непрерывная в каждой точке области (D), называется непрерывной в (D). Сумма, произведение, частное (при условии, что знаменатель не стремится к нулю), суперпозиция непрерывных функций являются непрерывными функциями.