9. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами

Линейным неоднородным дифференциальным уравнением (ЛНДУ) n-го порядка называется уравнение вида

(13)

где – известные функции,y(x) – искомая функция.

Теорема 2. Пусть – ФСР однородного уравнения (10) и пусть– некоторое частное решение уравнения (13). Тогда общее решение уравнения (13) имеет вид

где – произвольные постоянные; другими словами,общим решением уравнения (13) является сумма где– общее решение соответствующего однородного уравнения, а– некоторое частное решение уравнения (13).Пусть теперь в уравнении (13) являются постоянными величинами. Тогда общее решение однородного уравнения находим по правилам, изложенным в п.8. и задача интегрирования уравнения (13) сводится к отысканию некоторого частного решения этого уравнения.

Если в уравнении (13) имеет специальный вид

(14)

или

, (15)

то удается найти частное решение этого уравнения.

А. Пусть имеет вид (14) и числоне является корнем характеристического уравнения соответствующего однородного уравнения. Тогда частное решениеуравнения (13) ищется в виде

где коэффициенты находятся путем подстановкив уравнение (13).

Б. Пусть имеет вид (14) и числоявляется корнем кратности r характеристического уравнения соответствующего однородного уравнения. В этом случае частное решениеищется в виде

В. Пусть имеет вид (15) и числоне является корнем характеристического уравнения. Тогда частное решениеищется в виде

где .

Г. Пусть имеет вид (15) и числоявляется корнем кратности r характеристического уравнения. Тогда частное решение

где, как и прежде, .

Отметим теорему, которая бывает полезной при решении ЛНДУ.

Теорема 3. Пусть даны два ЛНДУ

,,

имеющие частными решениями исоответственно.

Тогда функция является частным решением уравнения

Пример 16. Решить задачу Коши

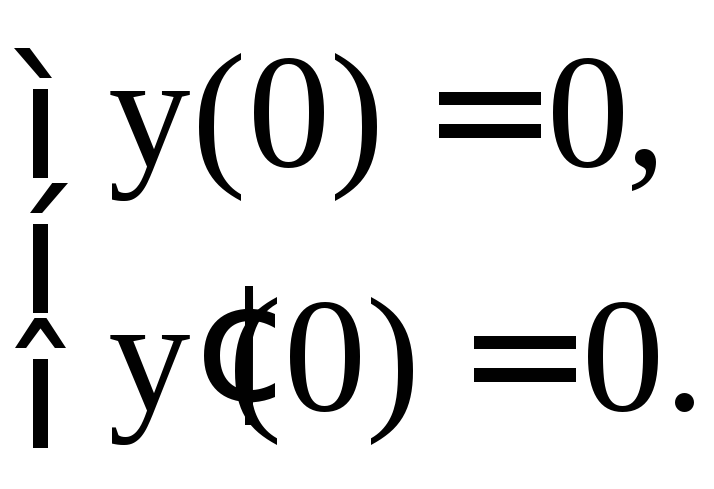
Решение. Сначала найдем общее решение дифференциального уравнения. Характеристическое уравнение имеет два простых вещественных корняпоэтому общим решением соответствующего однородного уравненияявляется

Найдем частное решение неоднородного уравнения. Так как числоне является корнем характеристического уравнения, а правая часть имеет вид (14) при, то решение надо искать по правилуА в виде Имеем

Подставим в исходное дифференциальное уравнение:

откуда находим .

Таким образом, общим решением дифференциального уравнения является

Для нахождения коэффициентов воспользуемся начальными условиями

Составим и решим систему уравнений

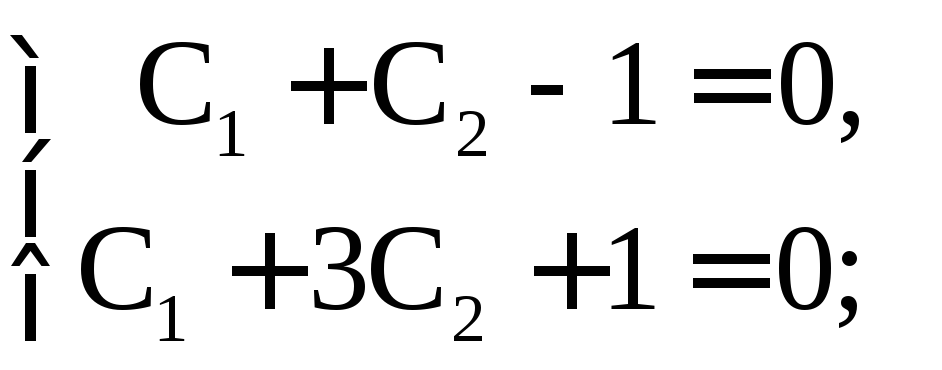
Итак, решением задачи Коши является функция

Пример 17. Найти частное решение уравнения удовлетворяющее начальным условиям

Решение. Общее решение этого уравнения имеет вид где– общее решение соответствующего однородного уравнения

(16)

а – некоторое частное решение нашего неоднородного уравнения. Характеристическое уравнение однородного уравнения (16) имеет видотсюда находим

Таким образом, Найдем

Правая часть уравнения имеет вид (15) при Так как числоне является корнем характеристического уравнения, то решениенадо искать по правилуВ в виде:

Для определения коэффициентов А и В подставим в исходное неоднородное уравнение. Имеем:

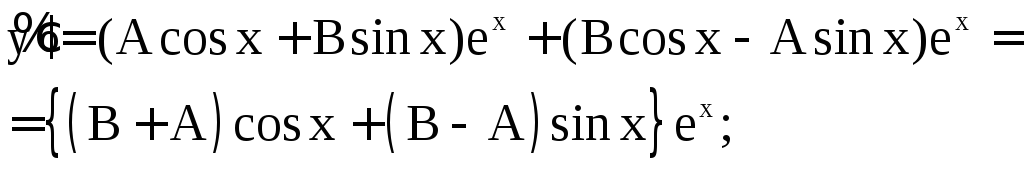
Сократим обе части на и приведем подобные:

Последнее равенство приводит к системе

Таким образом,

и общим решением неоднородного уравнения является

Для нахождения коэффициентов воспользуемся начальными условиями

Составим и решим систему уравнений

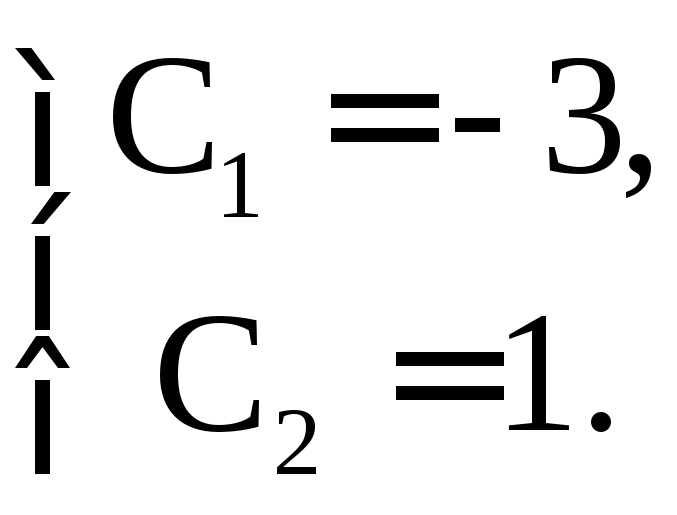
Итак, решением задачи Коши является функция

Пример 18. Решить уравнение

Решение. Характеристическое уравнение имеет простые корни. Общим решением соответствующего однородного уравнения является

Правая часть неоднородного уравнения имеет вид (15) при Числоявляется простым корнем характеристического уравнения. Поэтому частное решениенашего уравнения ищем по правилуГ

Имеем

Подставим в исходное уравнение:

Приравняв соответствующие коэффициенты, получим систему

Таким образом,

и общим решением исходного неоднородного уравнения является

Пример 19. Записать вид частного решения линейного неоднородного дифференциального уравнения (без нахождения коэффициентов):

Решение. a) Характеристическое уравнение имеет один коренькратностью 2. Числосовпадает с этим корнем, поэтому частное решениенеоднородного уравнения имеет вид

или

б) Характеристическое уравнение имеет два простых комплексных взаимно сопряженных корня:и. Числосовпадает с одним из этих корней, поэтому частное решениенеоднородного уравнения следует искать в виде

в) Характеристическое уравнение имеет два простых корня:Числоне   является корнем характеристического уравнения, следовательно, частное решениеимеет вид

Пример 20. Найти общее решение уравнения

Решение. Общее решение неоднородного уравнения имеет вид

где – общее решение однородного уравнения

а – некоторое частное решение исходного неоднородного уравнения.

Начнем с    нахождения   Характеристическое уравнениеимеет корниТаким образом, общее решение однородного уравнения имеет вид:

Так как число есть двукратный корень характеристического уравнения, а правая часть имеет вид (14) при, то решение надо искать по правилуБ в виде Для определения коэффициентов А и В подставимв исходное неоднородное уравнение. Имеем:

Это равенство приводит к системе:

Таким образом,

Общим решением нашего уравнения является

где – произвольные постоянные.