Задание 1.6

Найдите все нули многочлена и разложите его на неразложимые множители с действительными коэффициентами, если известен один из его нулей z₁ .

1) ,;

2) ,;

3) ,;

4) ,;

5) ,;

6) ,;

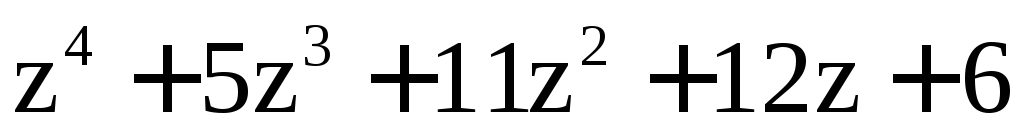7) ,;

8) ,;

9) ,;

10) ,;

11) ,;

12) ,;

13) ,;

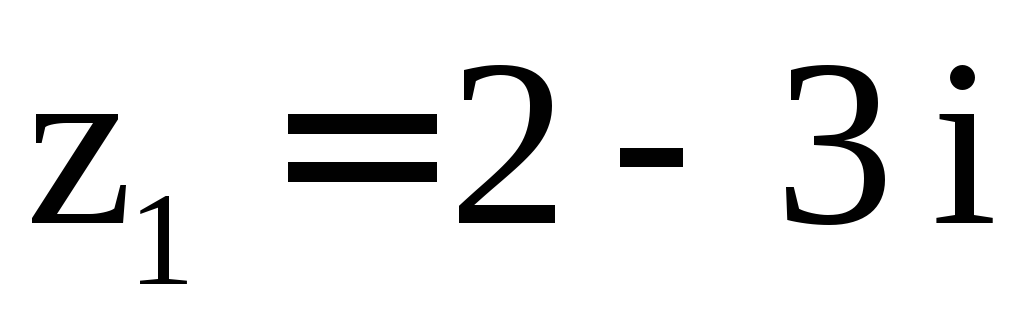14) ,;

15) ,;

16) ,;

17) ,;

18) ,;

19) ,;

20) ,;

21) ,;

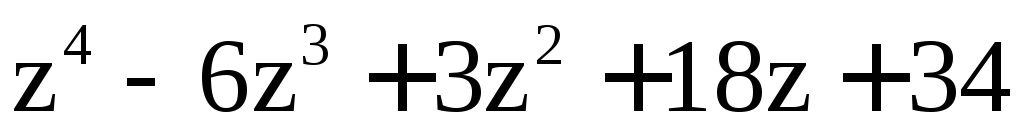22) ,;

23) ,;

24) ,;

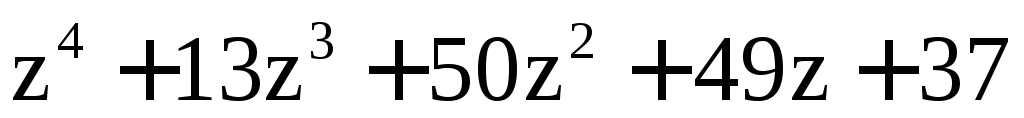25) ,;

26) ,;

27) ,;

28) ,;

29) ,;

30) ,.

Задание 1.7

Даны многочлены f(z) и g(z): а) подберите нули многочлена f(z) среди делителей свободного члена; б) разложите f(z) на линейные и неразложимые квадратичные множители с действительными коэффициентами; в) разложите f(z) на линейные множители с комплексными коэффициентами; г) разложите дробь g(z)/f(z) на сумму простейших дробей с действительными коэффициентами.

1) f(z) = z⁴ – 3z³ + z² + 4, g(z) = z² – 2z – 3;

2) f(z) = z⁴ – 4z³ + 2z² + z + 6, g(z) = z² – 2z – 4;

3) f(z) = z⁴ – 5z³ + 3z² +2 z + 8, g(z) = z² – 3z – 5;

4) f(z) = z⁴ – 2z² – 3 z – 2, g(z) = z² + z – 2;

5) f(z) = z⁴ – 6z³ + 4z² + 3z + 10, g(z) = z² – 5z – 6;

6) f(z) = z⁴ – z³ – 4z² – 5z – 3, g(z) = z² – 3z – 5;

7) f(z) = z⁴ – 7z³ + 5z² + 4z + 12, g(z) = z² – 6z – 5;

8) f(z) = z⁴ – 2z³ – 6z² – 7z – 4, g(z) = z² – 4z – 6;

9) f(z) = z⁴ – 3z³ – 8z² – 9z – 5, g(z) = z² – 5z – 7;

10) f(z) = z⁴ – 4z³ – 10z² – 11z – 6, g(z) = z² – 6z – 8;

11) f(z) = z⁴ – z³ – 2z² – 2z + 4, g(z) = z² – 2z – 3;

12) f(z) = z⁴ – 3z³ – 2z² + 2z + 12, g(z) = z² – 3z – 3;

13) f(z) = z⁴ – 2z³ – 3z² – 2z + 6, g(z) = z² – 3z – 2;

14) f(z) = z⁴ – 4z³ – 2z² + 4z + 16, g(z) = z² – 4z – 2;

15) f(z) = z⁴ – 3z³ – 4z² – 2z + 8, g(z) = z² + 4z –2;

16) f(z) = z⁴ – 5z³ – 2z² + 6z + 20, g(z) = z² – 5z – 5;

17) f(z) = z⁴ – 4z³ – 5z² – 2z + 10, g(z) = z² – 5z – 6;

18) f(z) = z⁴ – 6z³ – 2z² + 8z + 24, g(z) = z² – 6z –6;

19) f(z) = z⁴ + 3z³ + 2z² – 2z – 4, g(z) = z² – z – 3;

20) f(z) = z⁴ – 5z³ – 6z² – 2z + 12, g(z) = z² – 6z – 6;

21) f(z) = z⁴ + 2z³ – 2z² – 8z – 8, g(z) = z² – 2z – 4;

22) f(z) = z⁴ + z³ – 6z² – 14z – 12, g(z) = z² – 3z – 3;

23) f(z) = z⁴ – 3z³ + 4z² – 3z + 1, g(z) = z² – z – 3;

24) f(z) = z⁴ – z³ – 3z² + 4z – 4, g(z) = z² – 2z – 4;

25) f(z) = z⁴ – 4z³ + 6z² – 5z + 2, g(z) = z² – 2z + 4;

26) f(z) = z⁴ – 2z³ – 4z² + 5z – 6, g(z) = z² – 3z + 3;

27) f(z) = z⁴ – 5z³ + 8z² – 7z + 3, g(z) = z² + 3z – 3;

28) f(z) = z⁴ – 3z³ – 5z² + 6z – 8, g(z) = z² – 4z – 4;

29) f(z) = z⁴ – 6z³ + 10z² – 9z + 4, g(z) = z² + 4z – 4;

30) f(z) = z⁴ – 4z³ – 6z² + 7z – 10, g(z) = z² – 5z – 5.

31