2. Многочлены

Многочленом (или полиномом) степени ,называется функция

, (10)

где – известные комплексные числа (коэффициенты), при этом старший коэффициентотличен от 0,z – переменная комплексная величина. Степень многочлена f(z) обозначается deg f(z).

На множестве всех многочленов очевидным образом вводятся операции сложения и умножения. Число z₀ называется нулём многочлена f(z) , если f(z₀) = 0.

Теорема 1 (о делении многочленов). Для любых многочленов f(z) и g(z) существуют многочлены h(z) и r(z) такие, что:

1) f(z) = h(z) g(z) + r(z),

2) deg r(z) < deg g(z).

При этом h(z) и r(z) определяются однозначно.

Многочлен h(z) называется частным, а r(z) – остатком от деления f(z) на g(z). При этом оказывается, что deg f = deg g + deg h. Если r(z)  0, то говорят, что f(z) делится на g(z).

Теорема 2. Число z₀ является нулём многочлена f(z) в том и только в том случае, если f(z) делится на линейный многочлен (z – z₀).

Число z₀ называется нулём кратности m многочлена f(z), если f(z) делится на (z – z₀)^m и не делится на (z – z₀)^m+1. Можно дать другое, равносильное приведённому, определение: z₀ является нулём кратности m для многочлена f(z), если f(z) представим в виде

f(z) = (z – z₀)^m g(z), где g(z) – такой многочлен, что g(z₀)  0 .

Теорема 3 (основная теорема алгебры). Любой многочлен степени n  1 имеет ровно n нулей, если каждый нуль считать столько раз, какова его кратность.

Следствием основной теоремы алгебры является то, что если z₁, z₂, … , z_m – нули многочлена (1) кратностей k₁, k₂, … , k_m соответственно, то f(z) представим в виде

,

при этом , k₁ + k₂ + … +k_m = n .

Для того чтобы несократимая дробь (p – целое, q – натуральное) была нулём многочлена f(z) с целыми коэффициентами a_j, необходимо, чтобы число p было делителем свободного члена a_0, а число q – делителем старшего коэффициента а_n. В частности, если f(z) имеет целые коэффициенты a_j и a_n = 1, то рациональными нулями такого многочлена могут быть только целые числа, которые являются делителями свободного члена a₀ .

Теорема 4.  Если коэффициенты многочлена f(z) – действительные числа и – нуль f(z), тоz₀ =  – i также является нулём этого многочлена.

Из последней теоремы следует, что если f(z) – многочлен с действительными коэффициентами, то он представим в виде

, (11)

где z_j , p_j , q_j  –  действительные числа и квадратичные функции неразложимы (т.е. имеют отрицательный дискриминант), при.

При этом k₁ + k₂ + … + k_m + 2(r₁ + r₂ + … + r_s) = n .

Если f(z), g(z) – многочлены, то функция называется рациональной функцией или рациональной дробью. Рациональная дробьназывается правильной, еслиdeg g(z) < < deg f(z). Любую неправильную дробь можно представить в виде суммы многочлена и правильной рациональной дроби. Если – правильная рациональная дробь с действительными коэффициентами иf(z) имеет разложение (3), то h(z) допускает следующее представление в виде суммы простейших дробей:

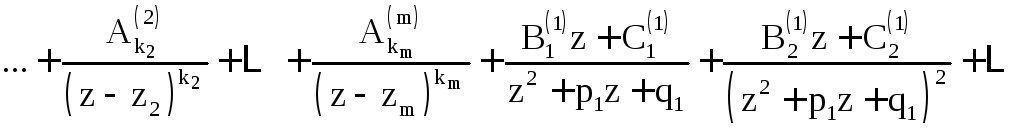
. (12)

Коэффициенты находятся путём приравнивания коэффициентов при одинаковых степенях z у многочлена g(z) и многочлена, который получается в числителе правой части (11) после приведения суммы к общему знаменателю (метод неопределённых коэффициентов).

Пример 6.    Найти все нули многочлена и разложить его на неразложимые множители с действительными коэффициентами, если известен один его нуль.

Решение. f(z) имеет действительные коэффициенты, поэтому наряду с z₁ = 2+i нулём f(z) является также z₂ = = 2–i. Значит, f(z) делится на.

Разделим f(z) на уголком

Таким образом, . Найдём нули второго множителя: z² + 2z + 10 = 0, z_3,4 = –1  3i.

Итак, нулями многочлена f(z) являются: z₁ = 2 + i, z₂ = 2 – i,

z₃ = –1 – 3i, z₄ = –1 + 3i. Многочлен f(z) разлагается на неразложимые множители (квадратные функции с отрицательными дискриминантами) следующим образом:

z⁴ – 2z³ + 7z² – 30z + 50 = (z² – 4z + 5)(z² +2z +10) .

Пример 7. Дан многочлен f(z) = z⁴ – 6z³ + 10z² + 2z – 15:

а) подобрать целые нули многочлена среди делителей свободного члена;

б) разложить f(z) на линейные и неразложимые квадратичные множители с действительными коэффициентами;

в) разложить f(z) на линейные множители с комплексными коэффициентами;

г) разложить дробь (2z – 3) / f(z) на простейшие дроби с действительными коэффициентами.

Решение. а) Делителями числа 15 являются: 1, 3, 5, 15.

В результате проверки убеждаемся, что z₁ = –1 является нулём f(z):

f(–1) = 0. Следовательно, f(z) делится на (z – z₁) = z + 1. Выполним деление

Имеем: f(z) = (z + 1) (z³ – 7z² +17z – 15). Найдём целые нули второго множителя среди делителей свободного члена (–15): 1; 3; 5; 15.

В результате проверки убеждаемся, что является нулём многочлена (z³ – 7z² +17z – 15) и, следовательно, многочлена f(z). Значит, f(z) делится на (z – z₁) (z – z₂) = (z + 1) (z – 3) = z² – 2z – 3. Разделим f(z) на этот квадратный трёхчлен:

Таким образом, f(z) = (z² – 2z – 3)(z² – 4z + 5). При этом второй множитель (z² – 4z +5) не имеет целых (и даже действительных) нулей. Итак, f(z) имеет лишь два целых нуля: z₁ = –1 и z₂ = 3.

б) Так как z² – 4z + 5 = 0 имеет лишь комплексные нули и, то искомым разложением будет уже полученное.

в) f(z) имеет 4 однократных (говорят, простых) нуля: z₁ = –1, z₂ = 3,

z₃ = 2 – i, z₄ = 2 + i. Старший коэффициент f(z) равен 1. Поэтому

f(z) = (z – z₁)(z – z₂ )(z – z₃)(z – z₄) или f(z) = (z + 1)(z – 3)

(z – 2 + i)(z –2– i).

г) Дробь (2z – 3)/f(z) является правильной. Имеем

.

Приведём последнюю сумму к общему знаменателю:

Так как f(z) равен знаменателю левой части, то получим равенство

A(z –3)(z²– 4z +5) + B(z + 1)(z²– 4z +5) + (Cz + D)(z +1)(z – 3)2z – 3.

Неизвестные коэффициенты А, В, С, D можно найти, раскрыв скобки в левой части, сгруппировав слагаемое по степеням z и приравняв соответствующие коэффициенты в левой и правой частях равенства, при этом получится система из 4-х линейных алгебраических уравнений:

(A + B + C)z³ + (– 7A – 3B – 2C + D)z² + (17A + B – 3C – 2D)z +

+(–15A + 5B – 3D) = 2z – 3.

Приравнивая коэффициенты при одинаковых степенях z, получаем систему

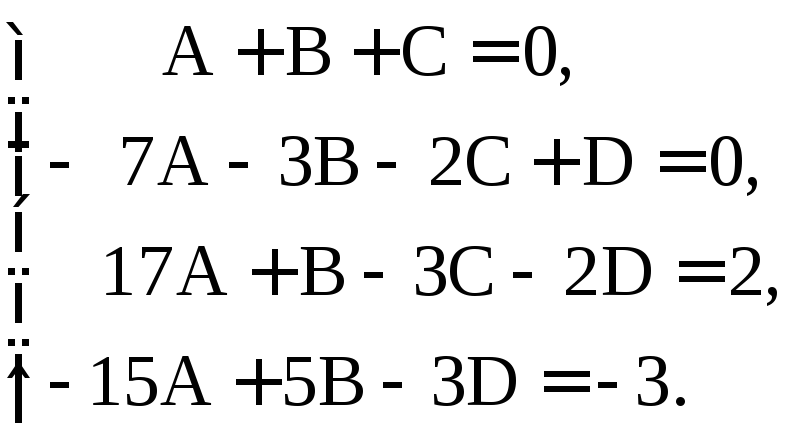
Решая её, находим A = 1/8, B = 3/8, C = –1/2, D =1. Итак, .