
- •1. Задачи, приводящие к оду
- •2.Оду 1-го порядка. Общие понятия
- •4. Однородное (относительно переменных) оду 1-го порядка
- •5. Линейные оду 1-го порядка, их интегрирование
- •6.Уравнение Бернулли, его интегрирование.
- •7.Уравнение в полных дифференциалах, его интегрирование.
- •8.Оду n-го порядка. Общая теория.
- •9.Оду высших порядков, допускающие понижение порядка.
- •10. Лоду n-го порядка. Общая теория
- •11. Теорема о структуре общего решения лоду n-го порядка (Если надо будет, то это свойство 5)
- •12.Лоду n-го порядка с постоянными коэффициентами, его решение
- •13.Лноду n-го порядка. Общая теория.
- •14.Теарема о структуре общего решения лноду n-го порядка.
- •15.Нахождение частных решений лноду n-го порядка по виду правой части.
- •16. Решение лноду n-го порядка методом вариации постоянных
- •17. Нормальные системы оду 1-го порядка. Общая теория
- •18. Приведение нормальной системы оду 1-го порядка к одному оду высшего порядка
- •19.Приведение оду высшего порядка к нормальной системе оду 1-го порядка.
- •20.Системы линейных оду 1-го порядка с постоянными коэффициентами. Метод Эйлера для решения этих систем.
15.Нахождение частных решений лноду n-го порядка по виду правой части.
 (Pm,
y,
Qm
– пишутся
с волнистым подчеркиванием сверху)
(Pm,
y,
Qm
– пишутся
с волнистым подчеркиванием сверху)
a0y(n) + a1y(n-1) + … + an-1y’ + any =f(x) (1)
1. пусть f(x) = Pm(x) = A0xm + A1xm-1+ … + Am-1x + Am
а) пусть an≠0, 0 не является корнем характеристического уравнения
 y(x)
= Qm(x)
= B0xm
+ B1xm-1
+ … + Bm
(2)
y(x)
= Qm(x)
= B0xm
+ B1xm-1
+ … + Bm
(2)
B0, B1 , … ,Bm – находятся методом неопределенных коэффициентов:
Выражение (2) подставляется в выражение (1) и приравниваются коэффициенты с одинаковыми степенями:
 xm
anB0
= A0
=> B0
= A0/an
xm
anB0
= A0
=> B0
= A0/an
xm-1 anB1 + mB0 = A1 => B1 = (A1 – mB0)/an
… и т.д.
б) an=0, это означет что 0 является корнем характеристического уравнения кратности α
 y(x)
= xα(B0xm
+ B1xm-1
+ … + Bm),
Bi
находятся аналогично случаю а
y(x)
= xα(B0xm
+ B1xm-1
+ … + Bm),
Bi
находятся аналогично случаю а
2. пусть f(x) = ePx(A0xm + … + Am)
Является ли Р корнем характеристического уравнения?
а) Р является корнем х.у. =>
 y(x)
= ePx(B0xm
+ … + Bm)
y(x)
= ePx(B0xm
+ … + Bm)
Bi – определяются методом неопр коэффициентов
б) Р является корнем х.у. кратности α
 y(x)
= xα
ePx(B0xm
+ … + Bm)
y(x)
= xα
ePx(B0xm
+ … + Bm)
Bi – определяются методом неопр коэффициентов



 3.
пусть f(x)
= ePx(Pm(x)cosqx
+ Qm(x)sinqx),
где Pm(x)
,Qm(x)
– многочлены из которых одинр степени
m,
а другой степени не большей m.
3.
пусть f(x)
= ePx(Pm(x)cosqx
+ Qm(x)sinqx),
где Pm(x)
,Qm(x)
– многочлены из которых одинр степени
m,
а другой степени не большей m.
Вопрос: является ли p+iq корнем х.у.?
а) p+iq – не является корнем х.у.
 y(x)
= ePx(Pm(x)cosqx
+Qm(x)sinqx),
где Pm
, Qm
– многочлены степени m
с неопределенными коэффициентами ,
которые определяются методом неопределенных
коэффициентов
y(x)
= ePx(Pm(x)cosqx
+Qm(x)sinqx),
где Pm
, Qm
– многочлены степени m
с неопределенными коэффициентами ,
которые определяются методом неопределенных
коэффициентов
б) р+iq является корнем х.у. кратности α
 y(x)
= xα
ePx(Pm(x)cosqx
+Qm(x)sinqx),
где Pm
, Qm
– многочлены степени m
с неопределенными коэффициентами ,
которые определяются методом неопределенных
коэффициентов
y(x)
= xα
ePx(Pm(x)cosqx
+Qm(x)sinqx),
где Pm
, Qm
– многочлены степени m
с неопределенными коэффициентами ,
которые определяются методом неопределенных
коэффициентов
16. Решение лноду n-го порядка методом вариации постоянных
Пусть имеем ЛНОДУ n-го порядка с некоторыми коэффициентами:
Yn+P1(x)yn-1+…+Pn-1(x)y’+Pn(x)y=f(x) (1)
Пусть найдено общее решение соответствующее ЛОДУ n-го порядка:
y(x)
=
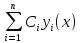 (2)
(2)
Ищем
решение в виде y(x)= (3)
(3)
Нахождение Ci(x):
СЛАУ
относительно Ci’(x),i=1,n

имеет
единственное решение, т.к.
 =W(x0)
=W(x0) 0
=> находимCi(x)
0
=> находимCi(x)
17. Нормальные системы оду 1-го порядка. Общая теория
Нормальные системы ОДУ 1-го порядка это системы вида:

Начальное условие: x1(t0)=x10 , x2(t0)=x20,…,xn(t0)=xn0 (2)
Определение 1: Решением нормальной системы (1) называется набор функций: ((x1(t),x2(t),…,xn(t)), который удовлетворяет каждому уравнению системы (1)
Задача (1)-(2) – задача Коши.
Теорема: (Существования и единственности задачи Коши)
Пусть fi непрерывна в окрестности начального условия, т.е. М0(t0,x10,…,xn0)
Пусть
 , где i,j=1,n
ограничены в некоторой окрестности
точки M0
=>
, где i,j=1,n
ограничены в некоторой окрестности
точки M0
=>
 (существует
и при том единственное) решение задачи
Коши (1)-(2).
(существует
и при том единственное) решение задачи
Коши (1)-(2).
Система может быть записана в матричном виде:

x’(t)=F (4) - матричный вид.
18. Приведение нормальной системы оду 1-го порядка к одному оду высшего порядка

исключим


Ф2(t,x1,…,xn)
(3) f(i)
 Дифференцируем
по переменной t:
Дифференцируем
по переменной t:

f(i)

Ф3(t,x1,…,xn)
(4)


Из системы (3)-(4)-(6) находим x2,x3,…,xn, выражая их через t,x’1,x’’2,…,xn и подставляем их в уравнение (6), в результате получим:

