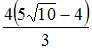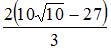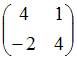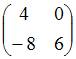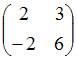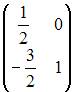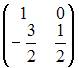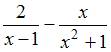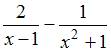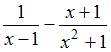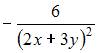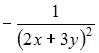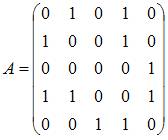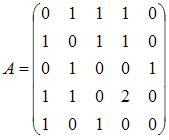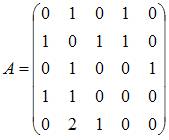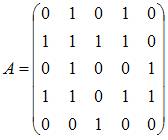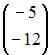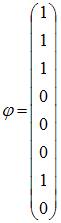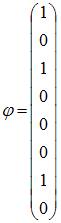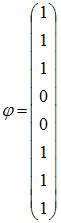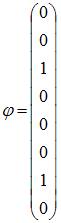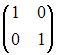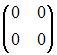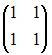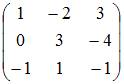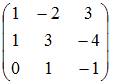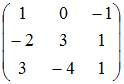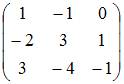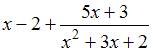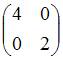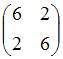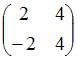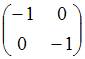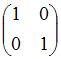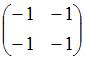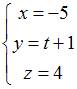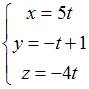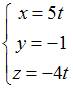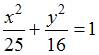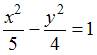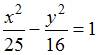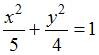![]() ЗАДАНИЕ
N 1
Тема:
Проверка статистических гипотез
ЗАДАНИЕ
N 1
Тема:
Проверка статистических гипотез
Соотношением
вида ![]() можно
определить …
можно
определить …
|
|
|
правостороннюю критическую область |
|
|
|
левостороннюю критическую область |
|
|
|
двустороннюю критическую область |
|
|
|
область принятия гипотезы |
ЗАДАНИЕ N 2 Тема: Элементы корреляционного анализа
При
построении выборочного уравнения парной
регрессии вычислены выборочный
коэффициент корреляции ![]() и
выборочные средние квадратические
отклонения
и
выборочные средние квадратические
отклонения ![]() .
Тогда выборочный коэффициент
регрессии
.
Тогда выборочный коэффициент
регрессии ![]() на
на ![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 3 Тема: Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема ![]() ,
гистограмма частот которой имеет
вид:
,
гистограмма частот которой имеет
вид:
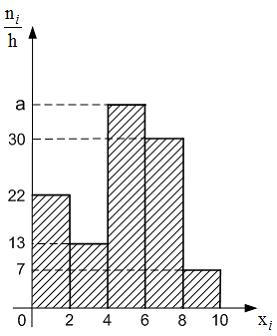 Тогда
значение a равно
…
Тогда
значение a равно
…
|
|
|
38 |
|
|
|
39 |
|
|
|
76 |
|
|
|
37 |
![]() ЗАДАНИЕ
N 4
Тема:
Интервальные оценки параметров
распределения
ЗАДАНИЕ
N 4
Тема:
Интервальные оценки параметров
распределения
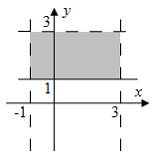
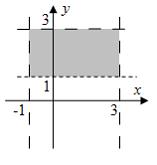
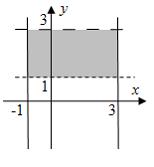
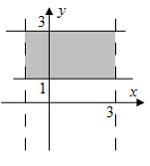
Дан
доверительный интервал ![]() для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при уменьшении объема
выборки этот доверительный интервал
может принять вид …
для
оценки математического ожидания
нормально распределенного количественного
признака. Тогда при уменьшении объема
выборки этот доверительный интервал
может принять вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Доверительный
интервал для оценки математического
ожидания нормально распределенного
количественного признака можно
представить в виде симметричного
интервала ![]() ,
где точечная оценка математического
ожидания
,
где точечная оценка математического
ожидания ![]() ,
а точность оценки
,
а точность оценки ![]() .
В случае уменьшения объема выборки
точность оценки ухудшается, то есть
значение
.
В случае уменьшения объема выборки
точность оценки ухудшается, то есть
значение ![]() будет
больше 2,13.
будет
больше 2,13.

ЗАДАНИЕ N 5 Тема: Операции над высказываниями
Из
трех логических выражений:
![]()
![]()
![]() эквивалентными
являются …
эквивалентными
являются …
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
все функции |
ЗАДАНИЕ N 6 Тема: Элементы комбинаторики
Из
города ![]() в
город
в
город ![]() ведут
5 дорог, из
в
ведут
5 дорог, из
в ![]() –
3 дороги, имеются также 2 дороги из
в
,
минуя
.
Из
в
можно
попасть ____ способом(-ами).
–
3 дороги, имеются также 2 дороги из
в
,
минуя
.
Из
в
можно
попасть ____ способом(-ами).
|
17
| |
Решение:
Из
города
в
город
можно
попасть ![]() способами,
из
в
–
с помощью
способами,
из
в
–
с помощью ![]() способов.
Тогда из
в
через
можно
попасть
способов.
Тогда из
в
через
можно
попасть ![]() способами
(по правилу произведения); а из
в
,
минуя
,
можно попасть
способами
(по правилу произведения); а из
в
,
минуя
,
можно попасть ![]() способами.
Поэтому
по правилу суммы общее число способов,
которыми можно попасть из города
в
город
,
равно:
способами.
Поэтому
по правилу суммы общее число способов,
которыми можно попасть из города
в
город
,
равно: ![]() .
.
ЗАДАНИЕ N 7 Тема: Декартово произведение множеств
Пусть
заданы два множества:
![]() ,
, ![]() .
Тогда
геометрическая интерпретация
множества
.
Тогда
геометрическая интерпретация
множества ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 8 Тема: Неориентированные графы
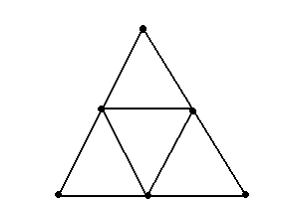
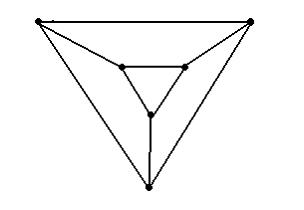
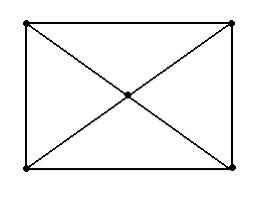
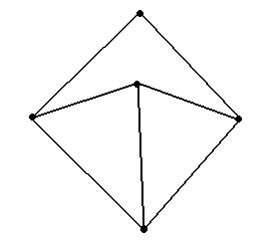
Эйлеровым является граф …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 9 Тема: Дифференциальная геометрия кривых
Траектория
движущейся точки задается уравнением 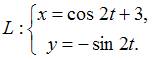 Тогда
значение касательного ускорения в
момент
Тогда
значение касательного ускорения в
момент ![]() равно
…
равно
…
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
Решение:
Касательное
ускорение на параметрически заданной
кривой вычисляется как
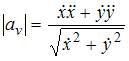 .
Вычислим
производные первого и второго
порядка.
.
Вычислим
производные первого и второго
порядка.
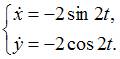
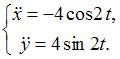 Найдем
Найдем 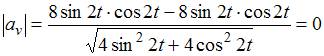 ,
при любых значениях
,
при любых значениях ![]() .
.
ЗАДАНИЕ N 10 Тема: Дифференциальная геометрия поверхностей
Точка
с координатами ![]() на
поверхности
на
поверхности ![]() является
…
является
…
|
|
|
гиперболической точкой |
|
|
|
параболической точкой |
|
|
|
эллиптической точкой |
|
|
|
точкой уплощения |
Решение:
Тип
точки на поверхности определяется по
виду соприкасающегося параболоида в
этой точке к поверхности.
Построим
соприкасающийся параболоид:
![]() .
Вычислим
частные производные второго
порядка:
.
Вычислим
частные производные второго
порядка:
![]() ;
; 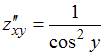 ;
; 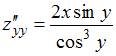 .
В
точке
;
.
В
точке
; ![]() ;
; ![]() .
Тогда
соприкасающийся параболоид
.
Тогда
соприкасающийся параболоид ![]() является
гиперболическим параболоидом, а сама
точка
относится
к гиперболическому типу.
является
гиперболическим параболоидом, а сама
точка
относится
к гиперболическому типу.
ЗАДАНИЕ N 11 Тема: Асимптоты кривой
Асимптоты
кривой 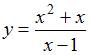 имеют
вид …
имеют
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Кривая
описывается соотношением  ,
то есть функция представлена в явном
виде.
В точке
функция
имеет разрыв, поэтому уравнение
вертикальной асимптоты имеет
вид:
.
Наклонные
или горизонтальные асимптоты определяются
уравнением
,
то есть функция представлена в явном
виде.
В точке
функция
имеет разрыв, поэтому уравнение
вертикальной асимптоты имеет
вид:
.
Наклонные
или горизонтальные асимптоты определяются
уравнением ![]() (для
горизонтальных асимптот
(для
горизонтальных асимптот ![]() ).
1.
Находим асимптоту
).
1.
Находим асимптоту ![]() при
при ![]() (правую
асимптоту):
(правую
асимптоту):
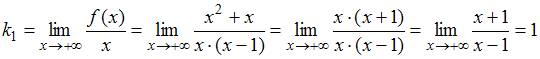 ,
,
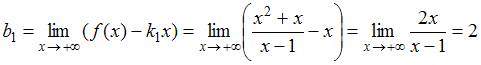 .
Следовательно,
уравнение правой асимптоты имеет
вид:
.
2.
Аналогично находим асимптоту
.
Следовательно,
уравнение правой асимптоты имеет
вид:
.
2.
Аналогично находим асимптоту ![]() при
при ![]() (левую
асимптоту):
(левую
асимптоту):
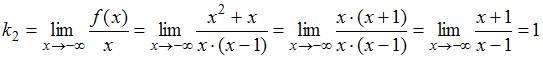 ,
,
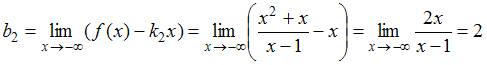 .
Следовательно,
уравнение левой асимптоты совпадает с
уравнением правой асимптоты и имеет
вид:
.
Таким
образом, прямые
и
являются
асимптотами заданной кривой.
.
Следовательно,
уравнение левой асимптоты совпадает с
уравнением правой асимптоты и имеет
вид:
.
Таким
образом, прямые
и
являются
асимптотами заданной кривой.
ЗАДАНИЕ N 12 Тема: Основные понятия топологии
Внешностью
множества ![]() в
топологическом пространстве
в
топологическом пространстве ![]() с
топологией
с
топологией ![]() является
…
является
…
|
|
|
пустое множество |
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Внешность M – это совокупность всех внутренних точек дополнения к множеству M, то есть входящих в дополнение к M с какой-либо своей окрестностью (открытым множеством). Дополнением является множество – закрытое множество, которое не содержит в себе ни одного открытого множества из данной топологии. Таким образом, внешностью множества в данном случае будет пустое множество.
ЗАДАНИЕ N 13 Тема: Непрерывность функции, точки разрыва
Для
функции ![]() точка
точка ![]() является
точкой …
является
точкой …
|
|
|
разрыва второго рода |
|
|
|
разрыва первого рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
ЗАДАНИЕ N 14 Тема: Дифференциалы и теоремы о дифференцируемых функциях
Приближенное
значение функции ![]() при
при ![]() ,
вычисленное с использованием дифференциала
первого порядка, равно …
,
вычисленное с использованием дифференциала
первого порядка, равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 15 Тема: Дифференциальное исчисление ФНП
Частная
производная ![]() функции
функции ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 16 Тема: Приложения определенного интеграла
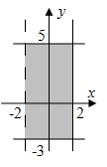
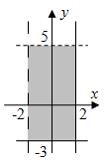
Площадь
фигуры, изображенной на рисунке
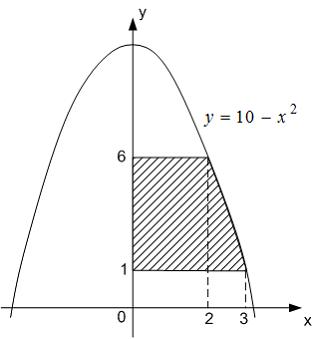 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 17 Тема: Поле направлений и изоклины
Поле
направлений дифференциального
уравнения ![]() определяется
неравенством …
определяется
неравенством …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Так
как поле направлений дифференциального
уравнения ![]() задано
в области определения функции двух
переменных
задано
в области определения функции двух
переменных ![]() ,
то для нахождения области задания поля
направлений следует решить
неравенство
,
то для нахождения области задания поля
направлений следует решить
неравенство ![]() .
Тогда
.
.
Тогда
.
ЗАДАНИЕ N 18 Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Общее
решение системы дифференциальных
уравнений 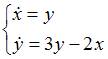 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 19 Тема: Задача Коши для дифференциального уравнения первого порядка
Функция ![]() является
общим решением дифференциального
уравнения 1-го порядка. Тогда для
начального условия
является
общим решением дифференциального
уравнения 1-го порядка. Тогда для
начального условия 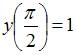 частное
решение этого уравнения имеет вид …
частное
решение этого уравнения имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 20 Тема: Дифференциальные уравнения с разделяющимися переменными
Дифференциальное
уравнение ![]() будет
уравнением с разделяющимися переменными
при значении
будет
уравнением с разделяющимися переменными
при значении ![]() ,
равном …
,
равном …
|
|
|
2 |
|
|
|
0 |
|
|
|
4 |
|
|
|
1 |
Решение:
Данное
уравнение можно представить в виде ![]() .
Это уравнение будет уравнением с
разделяющимися переменными при
.
Это уравнение будет уравнением с
разделяющимися переменными при ![]() ,
то есть при
,
то есть при ![]() .
Откуда
.
Откуда ![]() .
.
ЗАДАНИЕ N 21 Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков не меньше девяти, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Решение:
Для
вычисления события
(сумма
выпавших очков будет не меньше девяти)
воспользуемся формулой ![]() ,
где
,
где ![]() –
общее число возможных элементарных
исходов испытания, а m –
число элементарных исходов,
благоприятствующих появлению события A.
В нашем случае возможны
–
общее число возможных элементарных
исходов испытания, а m –
число элементарных исходов,
благоприятствующих появлению события A.
В нашем случае возможны ![]() элементарных
исходов испытания, из которых
благоприятствующими являются исходы
вида
элементарных
исходов испытания, из которых
благоприятствующими являются исходы
вида ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
то есть
,
то есть ![]() .
Следовательно,
.
Следовательно, ![]() .
.
ЗАДАНИЕ N 22 Тема: Числовые характеристики случайных величин
Непрерывная
случайная величина
задана
плотностью распределения вероятностей:
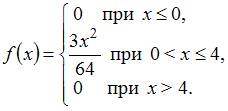 Тогда
ее математическое ожидание равно …
Тогда
ее математическое ожидание равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
ЗАДАНИЕ N 23 Тема: Законы распределения вероятностей дискретных случайных величин
Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна …
|
|
|
0,0081 |
|
|
|
0,081 |
|
|
|
0,06 |
|
|
|
0,0729 |
ЗАДАНИЕ N 24 Тема: Полная вероятность. Формулы Байеса
Имеются четыре урны, содержащие по 3 белых и 7 черных шаров, и шесть урн, содержащих по 8 белых и 2 черных шара. Из наудачу взятой урны вытаскивается один шар, который оказался белым. Тогда вероятность того, что этот шар был вынут из первой серии урн, равна …
|
|
|
0,20 |
|
|
|
0,80 |
|
|
|
0,72 |
|
|
|
0,40 |
Решение:
Предварительно
вычислим вероятность события A (вынутый
наудачу шар – белый) по формуле полной
вероятности: ![]() .
Здесь
.
Здесь ![]() –
вероятность того, что шар извлечен из
первой серии урн;
–
вероятность того, что шар извлечен из
первой серии урн; ![]() –
вероятность того, что шар извлечен из
второй серии урн;
–
вероятность того, что шар извлечен из
второй серии урн; ![]() –
условная вероятность того, что вынутый
шар белый, если из он извлечен из первой
серии урн;
–
условная вероятность того, что вынутый
шар белый, если из он извлечен из первой
серии урн; ![]() –
условная вероятность того, что вынутый
шар белый, если из он извлечен из второй
серии урн.
Тогда
–
условная вероятность того, что вынутый
шар белый, если из он извлечен из второй
серии урн.
Тогда ![]() .
Теперь
вычислим условную вероятность того,
что этот шар был извлечен из первой
серии урн, по формуле Байеса:
.
Теперь
вычислим условную вероятность того,
что этот шар был извлечен из первой
серии урн, по формуле Байеса:
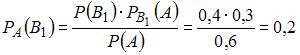 .
.
ЗАДАНИЕ N 25 Тема: Мера плоского множества
Мера
плоского множества 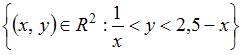 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
ЗАДАНИЕ N 26 Тема: Метрические пространства
Расстояние
между точками ![]() и
и ![]() в
метрике
в
метрике ![]() ,
где
,
где ![]() и
и ![]() ,
равно …
,
равно …
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
0 |
Решение:
![]() .
.
ЗАДАНИЕ N 27 Тема: Элементы теории множеств
Даны
три множества: ![]() ,
, ![]() и
и ![]() .
Тогда число элементов множества
.
Тогда число элементов множества ![]() равно
…
равно
…
|
1 | |
Решение:
Определим
множество ![]() и
выполним операцию пересечения
и
выполним операцию пересечения ![]() .
В результате получится множество
.
В результате получится множество ![]() ,
состоящее из одного элемента.
,
состоящее из одного элемента.
ЗАДАНИЕ N 28 Тема: Отображение множеств
Пусть
задано отображение ![]() .
Тогда
.
Тогда ![]() представляет
собой …
представляет
собой …
|
|
|
единичную окружность |
|
|
|
отрезок |
|
|
|
квадрат |
|
|
|
гиперболу |
ЗАДАНИЕ N 29 Тема: Линейные отображения
Пусть ![]() –
базис пространства
–
базис пространства ![]() .
Операторы
.
Операторы ![]() и
и ![]() этого
пространства заданы матрицами
этого
пространства заданы матрицами 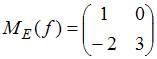 ;
; 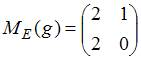 .
Тогда матрица оператора
.
Тогда матрица оператора ![]() равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
![]()
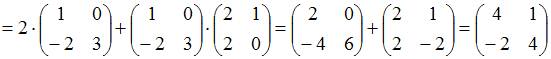 .
.
ЗАДАНИЕ N 30 Тема: Основные алгебраические структуры
Обратным
элементом для матрицы 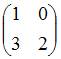 относительно
операции сложения матриц является …
относительно
операции сложения матриц является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 31 Тема: Дробно-рациональные функции
Множество
всех дробно-рациональных функций
образует поле ![]() относительно
обычных операций сложения и умножения
таких функций.
Пусть
относительно
обычных операций сложения и умножения
таких функций.
Пусть ![]() и
и ![]() ,
причем
,
причем 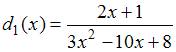 и
и 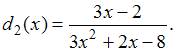 Тогда
числитель суммы
Тогда
числитель суммы ![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Разложим
на линейные множители знаменатели
дробно-рациональных функций ![]() и
и ![]() :
:
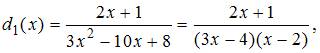
 Тогда
Тогда
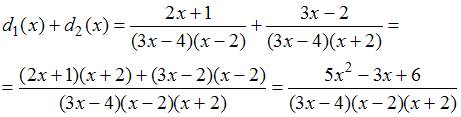 То
есть, числитель суммы
равен
.
То
есть, числитель суммы
равен
.
ЗАДАНИЕ N 32 Тема: Группы и подгруппы
На множестве целых чисел группу образует операция * определенная как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 33 Тема: Кривые второго порядка
Уравнение
директрисы параболы, проходящей через
точки ![]() ,
, ![]() и
симметричной относительно оси
и
симметричной относительно оси ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Каноническое
уравнение параболы, проходящей через
начало координат и симметричной
относительно оси
имеет
вид: ![]() ,
а уравнение директрисы:
,
а уравнение директрисы: ![]() .
Параметр
.
Параметр ![]() находится
из условия, что точка
принадлежит
параболе, то есть
находится
из условия, что точка
принадлежит
параболе, то есть ![]() ,
, ![]() .
Тогда уравнение директрисы параболы
примет вид:
.
.
Тогда уравнение директрисы параболы
примет вид:
.
ЗАДАНИЕ N 34 Тема: Прямоугольные координаты на плоскости
Точки ![]() и
и ![]() лежат
на одной прямой, параллельной оси
ординат. Расстояние между точками
и
лежат
на одной прямой, параллельной оси
ординат. Расстояние между точками
и ![]() равно
6. Тогда положительные координаты
точки
равны
…
равно
6. Тогда положительные координаты
точки
равны
…
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
, |
Решение:
Точки,
лежащие на одной прямой, параллельной
оси OY, имеют одинаковые абсциссы,
следовательно,
и ![]() .
Расстояние между двумя точками
.
Расстояние между двумя точками ![]() и
и ![]() находится
по формуле
находится
по формуле ![]() .
Тогда расстояние между точками
и
можно
найти как
.
Тогда расстояние между точками
и
можно
найти как ![]() .
Из
условия
.
Из
условия ![]() ,
получаем
,
получаем ![]() ,
или
,
или ![]() .
Следовательно,
.
Следовательно, ![]() ;
; ![]() .
Тогда положительные координаты
точки
равны:
,
.
.
Тогда положительные координаты
точки
равны:
,
.
ЗАДАНИЕ N 35 Тема: Плоскость в пространстве
Уравнение
плоскости, проходящей через
точку ![]() параллельно
векторам
параллельно
векторам ![]() и
и ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Уравнение
плоскости, проходящей через точку ![]() с
нормальным вектором
с
нормальным вектором ![]() ,
имеет вид:
,
имеет вид: ![]() .
В качестве нормального вектора плоскости
возьмем векторное произведение
векторов
.
В качестве нормального вектора плоскости
возьмем векторное произведение
векторов ![]() и
и ![]() .
Тогда
.
Тогда 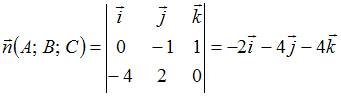 ,
или
,
или ![]() .
Подставляя в уравнение плоскости
координаты точки
и
вектора
.
Подставляя в уравнение плоскости
координаты точки
и
вектора ![]() ,
получим:
,
получим: ![]() или
.
или
.
ЗАДАНИЕ N 36 Тема: Прямая линия в пространстве
Острый
угол между прямыми 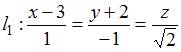 и
и  равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Угол
между прямыми ![]() и
и ![]() определяется
как угол между их направляющими
векторами:
определяется
как угол между их направляющими
векторами: ![]() и
и ![]() ,
который можно вычислить по
формуле:
,
который можно вычислить по
формуле:
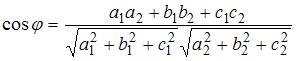 .
Тогда
.
Тогда 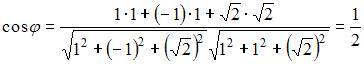 ,
то есть
,
то есть ![]() .
.
ЗАДАНИЕ N 37 Тема: Особые точки функции комплексного переменного
Число
особых точек функции 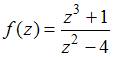 равно
…
равно
…
|
|
|
3 |
|
|
|
5 |
|
|
|
2 |
|
|
|
1 |
Решение:
Для
функции
точки ![]() –
полюсы первого порядка,
–
полюсы первого порядка,
![]() –
полюс первого порядка.
Следовательно,
число особых точек равно трем.
–
полюс первого порядка.
Следовательно,
число особых точек равно трем.
ЗАДАНИЕ N 38 Тема: Дифференцирование функции комплексного переменного
Если ![]() и
и ![]() ,
то мнимая часть производной этой
функции
,
то мнимая часть производной этой
функции ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 39 Тема: Области на комплексной плоскости
Все
точки ![]() комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке,
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке,
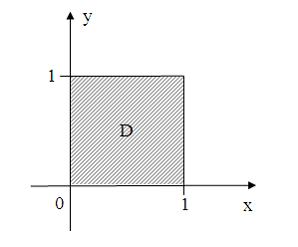 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 40 Тема: Операции над комплексными числами
Дано
комплексное число ![]() .
Тогда
.
Тогда ![]() равно
…
равно
…
|
|
|
16 |
|
|
|
|
|
|
|
2 |
|
|
|
|
Решение:
Если
комплексное число ![]() в
тригонометрической форме имеет вид
в
тригонометрической форме имеет вид ![]() ,
то по формуле Муавра
,
то по формуле Муавра ![]() ,
где
,
где ![]() –
натуральное число.
Запишем число
в
тригонометрической форме:
1) находим
модуль числа
–
натуральное число.
Запишем число
в
тригонометрической форме:
1) находим
модуль числа ![]() ;
2)
составляем систему уравнений для
нахождения аргумента
;
2)
составляем систему уравнений для
нахождения аргумента ![]() и
главного значения аргумента:
и
главного значения аргумента:
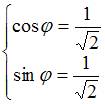 3)
находим главное значение аргумента
комплексного числа
,
которое равно
3)
находим главное значение аргумента
комплексного числа
,
которое равно![]() ;
4)
тогда
;
4)
тогда 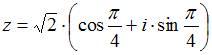 .
Следовательно,
.
Следовательно, 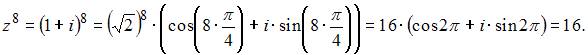
ЗАДАНИЕ N 1 Тема: Поле направлений и изоклины
Поле направлений дифференциального уравнения определяется неравенством …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Так как поле направлений дифференциального уравнения задано в области определения функции двух переменных , то для нахождения области задания поля направлений следует решить неравенство . Тогда .
ЗАДАНИЕ N 2 Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Решение
задачи Коши 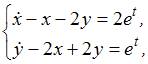
![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Решим
систему дифференциальных уравнений
методом исключения.
Из второго
уравнения находим ![]() ,
откуда
,
откуда![]() ;
после подстановки в первое уравнение
системы получим линейное неоднородное
дифференциальное уравнение второго
порядка с постоянными коэффициентами
;
после подстановки в первое уравнение
системы получим линейное неоднородное
дифференциальное уравнение второго
порядка с постоянными коэффициентами ![]() .
Характеристическое уравнение
.
Характеристическое уравнение ![]() имеет
два действительных корня:
имеет
два действительных корня: ![]() .
Таким корням соответствует общее решение
однородного дифференциального
уравнения
.
Таким корням соответствует общее решение
однородного дифференциального
уравнения ![]() .
Поскольку
правая часть исходного уравнения
.
Поскольку
правая часть исходного уравнения ![]() ,
то имеем уравнение со специальной правой
частью.
Так как
,
то имеем уравнение со специальной правой
частью.
Так как ![]() не
является корнем характеристического
уравнения, то частное решение
не
является корнем характеристического
уравнения, то частное решение ![]() неоднородного
уравнения будем искать в виде
неоднородного
уравнения будем искать в виде ![]() .
Найдя
производные первого и второго порядков
и подставив в уравнение
.
Найдя
производные первого и второго порядков
и подставив в уравнение ![]() ,
получим
,
получим ![]() .
Тогда
общее решение этого уравнения имеет
вид
.
Тогда
общее решение этого уравнения имеет
вид ![]() .
Дифференцируя полученное решение,
находим
.
Дифференцируя полученное решение,
находим ![]() и
и
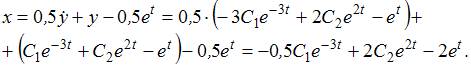 Значит,
общее решение системы уравнений имеет
вид
Значит,
общее решение системы уравнений имеет
вид ![]() .
Найдем
значения произвольных постоянных
.
Найдем
значения произвольных постоянных ![]() и
и ![]() ,
соответствующих исходной задаче Коши,
подставляя начальные условия в общее
решение. Получим систему уравнений
,
соответствующих исходной задаче Коши,
подставляя начальные условия в общее
решение. Получим систему уравнений 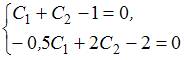 или
или 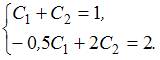 Решая
эту систему, находим значения постоянных
величин
Решая
эту систему, находим значения постоянных
величин ![]() .
Поэтому
решение задачи Коши имеет вид
.
Поэтому
решение задачи Коши имеет вид ![]() .
.
ЗАДАНИЕ N 3 Тема: Дифференциальные уравнения с разделяющимися переменными
Если угловой коэффициент касательной к кривой в любой ее точке вдвое больше углового коэффициента радиуса-вектора точки касания, то уравнение этой кривой будет иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 4 Тема: Задача Коши для дифференциального уравнения первого порядка
Частное
решение дифференциального уравнения ![]() ,
удовлетворяющее условию
,
удовлетворяющее условию ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Введем
замену ![]() ;
; ![]() .
Тогда уравнение
примет
вид
.
Тогда уравнение
примет
вид ![]() ,
или
,
или 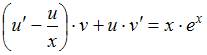 .
Пусть
.
Пусть ![]() .
Тогда
.
Тогда ![]() .
Подставим найденное значение
.
Подставим найденное значение ![]() в
уравнение
.
Получим:
в
уравнение
.
Получим: ![]() ,
то есть
,
то есть ![]() и
и ![]() .
Общее
решение примет вид
.
Общее
решение примет вид ![]() .
Подставив начальное условие,
получим
.
Подставив начальное условие,
получим ![]() .
Откуда
.
Откуда ![]() и
частное решение будет иметь вид
.
и
частное решение будет иметь вид
.
ЗАДАНИЕ N 5 Тема: Элементы теории множеств
Даны
два множества: ![]() и
и ![]() .
Тогда количество целых значений
.
Тогда количество целых значений ![]() ,
принадлежащих разности множеств
\
,
равно …
,
принадлежащих разности множеств
\
,
равно …
|
4 |
ЗАДАНИЕ N 6 Тема: Отображение множеств
Пусть
задано отображение ![]() .
Тогда
.
Тогда ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 7 Тема: Метрические пространства
Функция ![]() ,
где
,
где ![]() –
действительные числа, …
–
действительные числа, …
|
|
|
удовлетворяет всем трем аксиомам метрического пространства |
|
|
|
не удовлетворяет аксиоме тождества |
|
|
|
не удовлетворяет аксиоме симметрии |
|
|
|
не удовлетворяет аксиоме треугольника |
ЗАДАНИЕ N 8 Тема: Мера плоского множества
Мера
плоского множества ![]() равна
…
равна
…
|
|
|
4 |
|
|
|
1 |
|
|
|
2 |
|
|
|
0 |
Решение: Мера плоского множества равна площади соответствующей фигуры, то есть квадрата со стороной 2. Следовательно, мера этого множества равна 4.
ЗАДАНИЕ N 9 Тема: Плоскость в пространстве
Уравнение
плоскости, проходящей через точки ![]() ,
, ![]() и
и ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 10 Тема: Прямая линия в пространстве
Точка
пересечения прямой ![]() и
плоскости
и
плоскости ![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Запишем
уравнение прямой в параметрическом
виде:
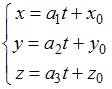 ,
то есть
,
то есть 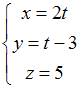 .
Подставим
полученные уравнения в уравнение
плоскости
.
Тогда
.
Подставим
полученные уравнения в уравнение
плоскости
.
Тогда ![]() ,
или
,
или ![]() .
Подставляя значение параметра
в
систему параметрических уравнений
.
Подставляя значение параметра
в
систему параметрических уравнений 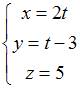 ,
найдем координаты точки пересечения
прямой и плоскости
.
,
найдем координаты точки пересечения
прямой и плоскости
.
ЗАДАНИЕ N 11 Тема: Прямоугольные координаты на плоскости
В
треугольнике с вершинами ![]() ,
, ![]() и
и ![]() проведена
медиана
проведена
медиана ![]() ,
длина которой равна …
,
длина которой равна …
|
|
|
4 |
|
|
|
|
|
|
|
16 |
|
|
|
|
Решение:
Точка
является
серединой отрезка ![]() .
Координаты середины отрезка определяются
по формулам
.
Координаты середины отрезка определяются
по формулам ![]() ,
, ![]() .
Подставляя в эти формулы координаты
точек
и
,
получим координаты точки
:
.
Подставляя в эти формулы координаты
точек
и
,
получим координаты точки
: ![]() ,
, ![]() .
Расстояние между точками
и
можно
найти по формуле
.
Расстояние между точками
и
можно
найти по формуле ![]() .
То
есть
.
То
есть ![]() .
.
ЗАДАНИЕ N 12 Тема: Кривые второго порядка
Асимптоты
гиперболы ![]() задаются
уравнениями …
задаются
уравнениями …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Асимптоты
гиперболы 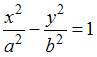 задаются
уравнениями вида
задаются
уравнениями вида ![]() .
Разделив обе части уравнения
на
36, получим каноническое уравнение
гиперболы:
.
Разделив обе части уравнения
на
36, получим каноническое уравнение
гиперболы: 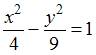 .
То есть
.
То есть ![]() и
и ![]() .
Тогда уравнения асимптот примут вид
.
.
Тогда уравнения асимптот примут вид
.
ЗАДАНИЕ N 13 Тема: Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема ![]() ,
полигон относительных частот которой
имеет вид:
,
полигон относительных частот которой
имеет вид:
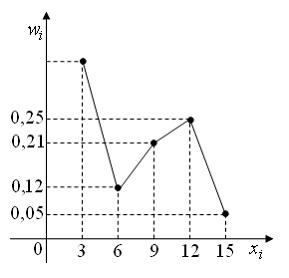 Тогда
число вариант
Тогда
число вариант ![]() в
выборке равно …
в
выборке равно …
|
|
|
37 |
|
|
|
63 |
|
|
|
100 |
|
|
|
36 |
ЗАДАНИЕ N 14 Тема: Проверка статистических гипотез
Основная
гипотеза имеет вид ![]() .
Тогда конкурирующей может являться
гипотеза …
.
Тогда конкурирующей может являться
гипотеза …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 15 Тема: Интервальные оценки параметров распределения
Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала , где точечная оценка математического ожидания , а точность оценки . В случае уменьшения объема выборки точность оценки ухудшается, то есть значение будет больше 2,13.
ЗАДАНИЕ N 16 Тема: Элементы корреляционного анализа
Выборочное
уравнение прямой линии регрессии ![]() на
на ![]() имеет
вид
имеет
вид ![]() .
Тогда выборочное среднее признака
равно
…
.
Тогда выборочное среднее признака
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Выборочное
уравнение прямой линии регрессии
на
имеет
вид ![]() .
Тогда выборочное среднее признака
равно
.
Тогда выборочное среднее признака
равно ![]() .
.
ЗАДАНИЕ N 17 Тема: Дифференцирование функции комплексного переменного
Если ![]() ,
то
,
то ![]() равно
…
равно
…
|
|
|
4 |
|
|
|
0 |
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 18 Тема: Области на комплексной плоскости
Все
точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке:
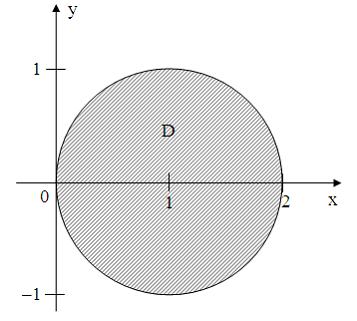 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 19 Тема: Операции над комплексными числами
Если ![]() и
и ![]() –
корни квадратного уравнения
–
корни квадратного уравнения ![]() ,
то
,
то ![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 20 Тема: Особые точки функции комплексного переменного
Для
функции 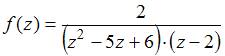 точка
точка ![]() является
…
является
…
|
|
|
полюсом второго порядка |
|
|
|
полюсом третьего порядка |
|
|
|
полюсом первого порядка |
|
|
|
существенно особой точкой |
Решение:
Порядок
полюса функции вида 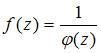 равен
порядку нуля
равен
порядку нуля ![]() .
Так
как
.
Так
как 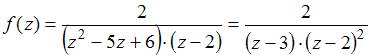 ,
то точка
будет
полюсом второго порядка.
,
то точка
будет
полюсом второго порядка.
ЗАДАНИЕ N 21 Тема: Асимптоты кривой
Асимптоты
кривой  имеют
вид …
имеют
вид …
|
|
|
и |
|
|
|
|
|
|
|
и |
|
|
|
и |
Решение:
Кривая
описывается соотношением 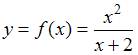 ,
то есть функция представлена в явном
виде.
В точке
функция
имеет разрыв второго рода, поэтому
уравнение вертикальной асимптоты имеет
вид:
.
Наклонные
или горизонтальные асимптоты определяются
уравнением
(для
горизонтальных асимптот
).
1.
Находим асимптоту
при
(правую
асимптоту):
,
то есть функция представлена в явном
виде.
В точке
функция
имеет разрыв второго рода, поэтому
уравнение вертикальной асимптоты имеет
вид:
.
Наклонные
или горизонтальные асимптоты определяются
уравнением
(для
горизонтальных асимптот
).
1.
Находим асимптоту
при
(правую
асимптоту):
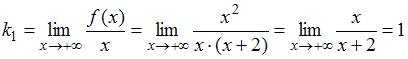 ,
,
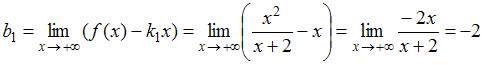 .
Следовательно,
уравнение правой асимптоты имеет
вид:
.
2.
Аналогично находим асимптоту
при
(левую
асимптоту):
.
Следовательно,
уравнение правой асимптоты имеет
вид:
.
2.
Аналогично находим асимптоту
при
(левую
асимптоту):
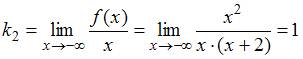 ,
,
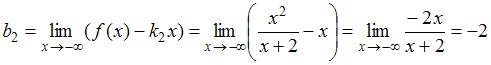 .
Следовательно,
уравнение левой асимптоты совпадает с
уравнением правой асимптотой и имеет
вид:
.
Таким
образом, прямые
и
являются
асимптотами заданной кривой.
.
Следовательно,
уравнение левой асимптоты совпадает с
уравнением правой асимптотой и имеет
вид:
.
Таким
образом, прямые
и
являются
асимптотами заданной кривой.
Математика i-exam вариант 4
ЗАДАНИЕ N 1 Тема: Области на комплексной плоскости
Все
точки
комплексной
плоскости, принадлежащие множеству
,
изображенному на рисунке:
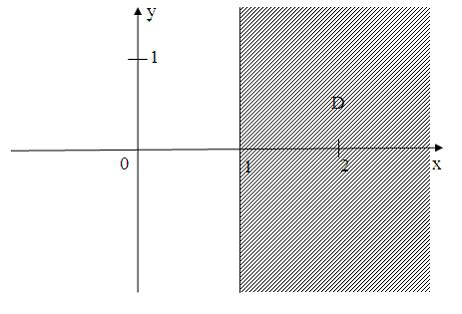 удовлетворяют
условию …
удовлетворяют
условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 2 Тема: Операции над комплексными числами
Произведение
комплексных чисел ![]() и
и ![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 3 Тема: Дифференцирование функции комплексного переменного
Если , то равно …
|
|
|
4 |
|
|
|
0 |
|
|
|
|
|
|
|
|
Решение:
Производная
функции
равна ![]() .
Тогда
.
Тогда ![]() .
.
ЗАДАНИЕ N 4 Тема: Особые точки функции комплексного переменного
Для
функции 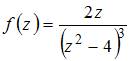 точка
является
…
точка
является
…
|
|
|
полюсом третьего порядка |
|
|
|
полюсом второго порядка |
|
|
|
полюсом первого порядка |
|
|
|
существенно особой точкой |
Решение:
Порядок
полюса функции вида
равен
порядку нуля
.
Имеем 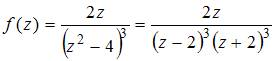 ,
поэтому
точка
будет
полюсом третьего порядка.
,
поэтому
точка
будет
полюсом третьего порядка.
ЗАДАНИЕ N 5 Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Общее
решение системы дифференциальных
уравнений 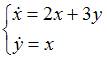 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Решим
систему дифференциальных уравнений
методом исключения.
Из второго
уравнения находим производную ![]() и
после подстановки выражений для
и
и
после подстановки выражений для
и ![]() в
первое уравнение системы получим
линейное однородное дифференциальное
уравнение второго порядка с постоянными
коэффициентами
в
первое уравнение системы получим
линейное однородное дифференциальное
уравнение второго порядка с постоянными
коэффициентами ![]() .
Характеристическое
уравнение
.
Характеристическое
уравнение ![]() имеет
два действительных корня:
имеет
два действительных корня: ![]() .
Таким
корням соответствует общее решение
однородного дифференциального
уравнения
.
Таким
корням соответствует общее решение
однородного дифференциального
уравнения ![]() .
Дифференцируя полученное решение,
находим
.
Дифференцируя полученное решение,
находим ![]() .
Тогда
общее решение системы уравнений имеет
вид
.
.
Тогда
общее решение системы уравнений имеет
вид
.
ЗАДАНИЕ N 6 Тема: Дифференциальные уравнения с разделяющимися переменными
Дифференциальное
уравнение ![]() будет
уравнением с разделяющимися переменными
при значении
,
равном …
будет
уравнением с разделяющимися переменными
при значении
,
равном …
|
|
|
2 |
|
|
|
4 |
|
|
|
0 |
|
|
|
1 |
Решение:
Данное
уравнение можно представить в виде: ![]() .
Это
уравнение будет уравнением с разделяющимися
переменными при
.
Это
уравнение будет уравнением с разделяющимися
переменными при ![]() ,
то есть при
.
Откуда
.
,
то есть при
.
Откуда
.
ЗАДАНИЕ N 7 Тема: Поле направлений и изоклины
Дано
дифференциальное уравнение 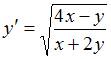 .
Тогда отрезок соответствующего ему
поля направлений в точке
.
Тогда отрезок соответствующего ему
поля направлений в точке ![]() образует
с осью
угол
при
образует
с осью
угол
при ![]() равном…
равном…
|
|
|
2 |
|
|
|
14 |
|
|
|
|
|
|
|
|
Решение:
Так
как дифференциальное уравнение имеет
вид ![]() ,
то угол
определяется
из равенства
,
то угол
определяется
из равенства ![]() ,
где
,
где ![]() –
координаты точки
.
В
рассматриваемом случае
–
координаты точки
.
В
рассматриваемом случае 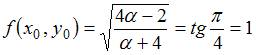 ,
то есть
,
то есть ![]() .
Следовательно,
.
.
Следовательно,
.
ЗАДАНИЕ N 8 Тема: Задача Коши для дифференциального уравнения первого порядка
Решение
задачи Коши ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 9 Тема: Дробно-рациональные функции
Разложение
дробно-рациональной функции 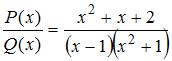 на
простые дроби над полем вещественных
чисел имеет вид …
на
простые дроби над полем вещественных
чисел имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 10 Тема: Основные алгебраические структуры
Алгеброй является …
|
|
|
множество рациональных чисел и операция умножения |
|
|
|
пустое множество и операция пересечения |
|
|
|
множество натуральных чисел и операция векторного произведения |
|
|
|
множество целых чисел и отношение порядка |
Решение:
Алгеброй
называется пара ![]() ,
состоящая из непустого множества
и
множества
,
состоящая из непустого множества
и
множества ![]() ,
заданных на нем операций.
Тогда пустое
множество и операция пересечения не
являются алгеброй, так как множество
не
может быть пустым.
Множество натуральных
чисел и операция векторного произведения
не являются алгеброй, так как операция
векторного произведения задается на
множестве векторов, а не на множестве
натуральных чисел.
Множество целых
чисел и отношение порядка не являются
алгеброй, так как не задана ни одна
операция.
Множество рациональных
чисел и операция умножения являются
алгеброй.
,
заданных на нем операций.
Тогда пустое
множество и операция пересечения не
являются алгеброй, так как множество
не
может быть пустым.
Множество натуральных
чисел и операция векторного произведения
не являются алгеброй, так как операция
векторного произведения задается на
множестве векторов, а не на множестве
натуральных чисел.
Множество целых
чисел и отношение порядка не являются
алгеброй, так как не задана ни одна
операция.
Множество рациональных
чисел и операция умножения являются
алгеброй.
ЗАДАНИЕ N 11 Тема: Группы и подгруппы
Операция «+» – сложения образует группу на множестве …
|
|
|
целых четных чисел |
|
|
|
натуральных чисел |
|
|
|
целых нечетных чисел |
|
|
|
действительных чисел без нуля |
Решение:
Множество
целых четных чисел с введенной операцией
сложения образует группу. Множество
натуральных чисел не группа, так как,
например, ![]() не
имеет противоположного элемента.
Множество целых нечетных не имеет
нулевого элемента, как и множество
действительных чисел без нуля.
не
имеет противоположного элемента.
Множество целых нечетных не имеет
нулевого элемента, как и множество
действительных чисел без нуля.
ЗАДАНИЕ N 12 Тема: Линейные отображения
Линейным отображением пространства трехмерных векторов на пространство двумерных векторов является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Линейным
называется отображение
удовлетворяющее
условиям:
![]() ,
,
![]() .
Проверим
на линейность отображение
:
.
Проверим
на линейность отображение
:
![]() ,
,
![]() ,
Следовательно
,
Следовательно ![]() –
первое условие не выполнено, а значит
не
является линейным отображением.
Для
отображения
проверим
выполнение второго условия:
–
первое условие не выполнено, а значит
не
является линейным отображением.
Для
отображения
проверим
выполнение второго условия:
![]() Условие
не выполняется, значит
не
линейное отображение.
Проверим
выполнение второго условия для
отображения
:
Условие
не выполняется, значит
не
линейное отображение.
Проверим
выполнение второго условия для
отображения
:
![]() Следовательно,
данное отображение не является
линейным.
Проверим выполнение условий
линейности для отображения
:
Следовательно,
данное отображение не является
линейным.
Проверим выполнение условий
линейности для отображения
:
![]() ,
,
![]() ,
Следовательно
,
Следовательно ![]() –
первое условие выполнено.
–
первое условие выполнено.
![]() –
второе условие выполнено. Поэтому
является
линейным отображением.
–
второе условие выполнено. Поэтому
является
линейным отображением.
ЗАДАНИЕ N 13 Тема: Прямая линия в пространстве
Прямая ![]() параллельна
плоскости
параллельна
плоскости ![]() ,
если параметр
,
если параметр ![]() равен
…
равен
…
|
|
|
– 11 |
|
|
|
– 7 |
|
|
|
7 |
|
|
|
11 |
ЗАДАНИЕ N 14 Тема: Кривые второго порядка
Уравнением
кривой второго порядка ![]() на
плоскости определяется …
на
плоскости определяется …
|
|
|
эллипс |
|
|
|
гипербола |
|
|
|
парабола |
|
|
|
пара пересекающихся прямых |
Решение:
Выделим
в уравнении
полный
квадрат по переменной
: ![]() ,
или
,
или ![]() .
Разделив обе части этого уравнения на
10, получим уравнение вида:
.
Разделив обе части этого уравнения на
10, получим уравнение вида: 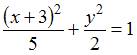 ,
которое на плоскости определяет эллипс.
,
которое на плоскости определяет эллипс.
ЗАДАНИЕ N 15 Тема: Прямоугольные координаты на плоскости
Даны
точки ![]() и
и ![]() .
Тогда координаты точки
.
Тогда координаты точки ![]() ,
симметричной точке
относительно
точки
,
равны …
,
симметричной точке
относительно
точки
,
равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 16 Тема: Плоскость в пространстве
Плоскость,
проходящая через точки ![]() и
и ![]() параллельно
оси
параллельно
оси ![]() ,
задается уравнением …
,
задается уравнением …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Общее
уравнение плоскости, параллельной
оси
,
имеет вид: ![]() .
Точки
и
лежат
в искомой плоскости, следовательно, их
координаты удовлетворяют уравнению
:
.
Точки
и
лежат
в искомой плоскости, следовательно, их
координаты удовлетворяют уравнению
: 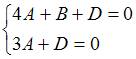 ,
отсюда
,
отсюда ![]() ,
, ![]() .
Подставим найденные значения в уравнение
плоскости:
.
Подставим найденные значения в уравнение
плоскости: ![]() или
или ![]() ,
то есть
.
,
то есть
.
ЗАДАНИЕ N 17 Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – десять, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
ЗАДАНИЕ N 18 Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная
случайная величина
задана
законом распределения вероятностей:
 Тогда
вероятность
Тогда
вероятность ![]() равна
…
равна
…
|
|
|
0,8 |
|
|
|
0,3 |
|
|
|
0,7 |
|
|
|
0,4 |
ЗАДАНИЕ N 19 Тема: Полная вероятность. Формулы Байеса
Банк выдает 40% всех кредитов юридическим лицам, а 60% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,1; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило физическое лицо, равна …
|
|
|
|
|
|
|
|
|
|
|
0,07 |
|
|
|
0,05 |
Решение:
Предварительно
вычислим вероятность события A (выданный
кредит не будет погашен в срок) по формуле
полной вероятности:
.
Здесь
–
вероятность того, что кредит был выдан
юридическому лицу;
–
вероятность того, что кредит был выдан
физическому лицу;
–
условная вероятность того, что кредит
не будет погашен в срок, если он был
выдан юридическому лицу;
–
условная вероятность того, что кредит
не будет погашен в срок, если он был
выдан физическому лицу. Тогда
![]() .
Теперь
вычислим условную вероятность того,
что этот кредит не погасило физическое
лицо, по формуле Байеса:
.
Теперь
вычислим условную вероятность того,
что этот кредит не погасило физическое
лицо, по формуле Байеса:
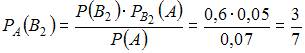 .
.
ЗАДАНИЕ N 20 Тема: Числовые характеристики случайных величин
Математическое
ожидание дискретной случайной величины
,
заданной законом распределения
вероятностей:
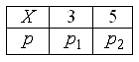 равно
4,4. Тогда значение вероятности
равно
4,4. Тогда значение вероятности ![]() равно
…
равно
…
|
|
|
0,7 |
|
|
|
0,3 |
|
|
|
0,6 |
|
|
|
0,4 |
Решение:
Математическое
ожидание дискретной случайной величины
вычисляется по формуле 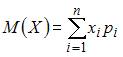 .
Тогда
.
Тогда ![]() .
А с учетом условия
.
А с учетом условия ![]() получаем
систему уравнений:
получаем
систему уравнений:
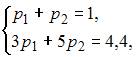 решение
которой имеет вид:
решение
которой имеет вид: ![]() ,
, ![]() .
.
ЗАДАНИЕ N 21 Тема: Интервальные оценки параметров распределения
Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 22 Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема , гистограмма частот которой имеет вид: Тогда значение a равно …
|
|
|
38 |
|
|
|
39 |
|
|
|
76 |
|
|
|
37 |
ЗАДАНИЕ N 23 Тема: Проверка статистических гипотез
Для
проверки нулевой гипотезы ![]() при
заданном уровне значимости
при
заданном уровне значимости ![]() выдвинута
конкурирующая гипотеза
выдвинута
конкурирующая гипотеза ![]() .
Тогда область принятия гипотезы может
иметь вид …
.
Тогда область принятия гипотезы может
иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 24 Тема: Элементы корреляционного анализа
При построении выборочного уравнения парной регрессии вычислены выборочный коэффициент корреляции и выборочные средние квадратические отклонения . Тогда выборочный коэффициент регрессии на равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Выборочный
коэффициент регрессии
на
вычисляется
по формуле 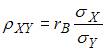 .
Тогда
.
Тогда 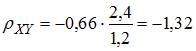 .
.
ЗАДАНИЕ N 25 Тема: Отображение множеств
Отображение ![]() действует
по правилу:
действует
по правилу: 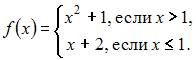 Тогда
Тогда ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Так
как ![]() при
при ![]() и
и ![]() при
при ![]() ,
то
,
то ![]() .
.
ЗАДАНИЕ N 26 Тема: Элементы теории множеств
Даны
три множества: ![]() ,
, ![]() и
и ![]() .
Тогда число элементов множества
.
Тогда число элементов множества ![]() равно
…
равно
…
|
3 | |
Решение:
Выполним
операцию в скобках, то есть определим
множество ![]() .
Теперь выполним вычитание, в результате
которого получится множество чисел,
принадлежащих
.
Теперь выполним вычитание, в результате
которого получится множество чисел,
принадлежащих ![]() ,
но без чисел множества
:
,
но без чисел множества
: ![]() .
Таким образом, множество
содержит
три элемента.
.
Таким образом, множество
содержит
три элемента.
ЗАДАНИЕ N 27 Тема: Метрические пространства
Расстояние между точками и в метрике , где и , равно …
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
0 |
ЗАДАНИЕ N 28 Тема: Мера плоского множества
Мера
плоского множества ![]() ,
где А=
и
,
где А=
и ![]() равна
…
равна
…
|
|
|
|
|
|
|
4 |
|
|
|
0 |
|
|
|
1 |
Решение:
Мера
плоского множества
равна
площади соответствующей фигуры, то есть
квадрата со стороной 2. Мера плоского
множества ![]() равна
площади соответствующей фигуры, то есть
круга с радиусом 1. Так как круг целиком
лежит внутри квадрата, то искомая мера
равна
.
равна
площади соответствующей фигуры, то есть
круга с радиусом 1. Так как круг целиком
лежит внутри квадрата, то искомая мера
равна
.
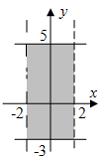
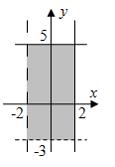
ЗАДАНИЕ N 29 Тема: Приложения определенного интеграла
Площадь
фигуры, изображенной на рисунке
 равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 30 Тема: Дифференциалы и теоремы о дифференцируемых функциях
Дана
функция ![]() .
Тогда меньший действительный корень
производной этой функции принадлежит
промежутку …
.
Тогда меньший действительный корень
производной этой функции принадлежит
промежутку …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Эта
функция представляет собой полином
6-го порядка и дифференцируема на всей
числовой оси. Согласно теореме Ролля
между двумя корнями (нулями) этой функции
находится по крайней мере один корень
ее производной. Поскольку ![]() представляет
собой полином (5-го порядка), то между
двумя корнями функции
представляет
собой полином (5-го порядка), то между
двумя корнями функции ![]() находится
ровно один корень ее производной
.
Найдем
корни функции
:
находится
ровно один корень ее производной
.
Найдем
корни функции
: ![]() .
Тогда меньший действительный корень
функции
принадлежит
интервалу
.
.
Тогда меньший действительный корень
функции
принадлежит
интервалу
.
ЗАДАНИЕ N 31 Тема: Непрерывность функции, точки разрыва
Для функции точка является точкой …
|
|
|
разрыва второго рода |
|
|
|
разрыва первого рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
Решение:
Вычислим
односторонние пределы функции
в
точке
:
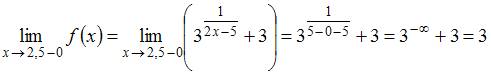 ,
,
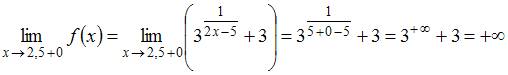 .
Так
как один из односторонних пределов в
точке
,
а именно
.
Так
как один из односторонних пределов в
точке
,
а именно ![]() ,
то точка
является
точкой разрыва второго рода.
,
то точка
является
точкой разрыва второго рода.
ЗАДАНИЕ N 32 Тема: Дифференциальное исчисление ФНП
Частная
производная второго порядка ![]() функции
функции ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
При
вычислении частной производной
функции ![]() по
одной из переменных другую переменную
рассматриваем как постоянную величину.
Тогда
по
одной из переменных другую переменную
рассматриваем как постоянную величину.
Тогда
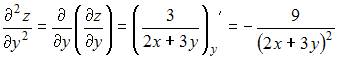 .
.
ЗАДАНИЕ N 33 Тема: Элементы комбинаторики
В урне находятся 10 белых, 15 красных, 20 голубых шаров. Все шары пронумерованы. Сколькими различными способами можно взять из урны три шара разных цветов?
|
3000 | |
Решение:
Возьмем
один белый шар. Это действие можно
выполнить 10 способами (по числу различных
белых шаров в урне). К выбранному белому
шару присоединим красный шар, который
можно взять 15 различными способами (по
числу различных красных шаров в урне).
К выбранной присоединим голубой шар,
который можно взять 20 способами (по
числу различных голубых шаров в урне).
Таким образом, можно образовать различные
тройки разноцветных шаров. Число
различных способов выбора троек
разноцветных шаров совпадает с числом
различных трех действий и по правилу
умножения равно:
![]()
ЗАДАНИЕ N 34 Тема: Операции над высказываниями
Для
функции ![]() ,
заданной таблицей,
,
заданной таблицей,
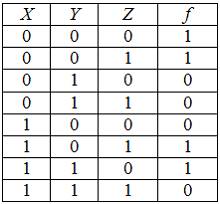 СДНФ
имеет вид …
СДНФ
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
СДНФ
будет выглядеть следующим образом:
![]()
ЗАДАНИЕ N 35 Тема: Неориентированные графы
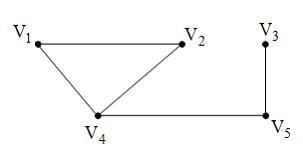
Для
графа, изображенного на
рисунке,
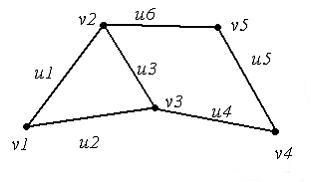 последовательность
последовательность ![]() является
…
является
…
|
|
|
маршрутом |
|
|
|
цепью |
|
|
|
циклом |
|
|
|
деревом |
ЗАДАНИЕ N 36 Тема: Декартово произведение множеств
Даны
множества ![]() ,
, ![]() и
и ![]() .
Тогда число элементов декартова
произведения множеств
.
Тогда число элементов декартова
произведения множеств ![]() равно…
равно…
|
|
|
8 |
|
|
|
6 |
|
|
|
12 |
|
|
|
4 |
Решение:
Декартово
произведение множеств – это множество,
состоящее из упорядоченных пар элементов,
первым элементом которых являются
элементы первого множества, вторым –
элементы второго, то есть 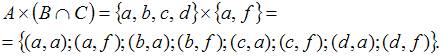 Данное
множество содержит восемь элементов.
Данное
множество содержит восемь элементов.
ЗАДАНИЕ N 37 Тема: Дифференциальная геометрия поверхностей
Первая
квадратичная форма поверхности  имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Запишем
поверхность в виде вектор-функции ![]() и
вычислим частные производные:
и
вычислим частные производные: ![]() ,
, ![]() .
Коэффициенты
первой квадратичной формы
.
Коэффициенты
первой квадратичной формы ![]() определим
по формулам:
определим
по формулам:
![]() ;
;
![]() ;
;
![]() .
Тогда
.
Тогда ![]() ;
;
![]() ;
;
![]() .
Таким
образом,
.
.
Таким
образом,
.
ЗАДАНИЕ N 38 Тема: Дифференциальная геометрия кривых
Длина
дуги кривой 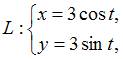 при
при 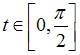 ,
равна …
,
равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,14 |
ЗАДАНИЕ N 39 Тема: Асимптоты кривой
Асимптоты
кривой ![]() имеют
вид …
имеют
вид …
Математика i-exam вариант 3
ЗАДАНИЕ N 1 Тема: Приложения определенного интеграла
Объем
тела, полученного вращением вокруг
оси
криволинейной
трапеции, ограниченной параболой ![]() и
осью
,
равен …
и
осью
,
равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 2 Тема: Непрерывность функции, точки разрыва
Количество
точек разрыва функции 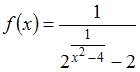 равно
…
равно
…
|
|
|
4 |
|
|
|
2 |
|
|
|
1 |
|
|
|
3 |
Решение:
Точку ![]() называют
точкой разрыва функции
называют
точкой разрыва функции ![]() ,
если она не является непрерывной в этой
точке. В частности, точками разрыва
данной функции являются точки, в которых
знаменатели равны нулю. То есть
,
если она не является непрерывной в этой
точке. В частности, точками разрыва
данной функции являются точки, в которых
знаменатели равны нулю. То есть ![]() ,
и
,
и ![]() .
Тогда
.
Тогда
![]() ,
,
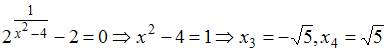 .
Следовательно,
получили четыре точки разрыва функции.
.
Следовательно,
получили четыре точки разрыва функции.
ЗАДАНИЕ N 3 Тема: Дифференциальное исчисление ФНП
Смешанная
частная производная второго
порядка ![]() функции
функции ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 4 Тема: Дифференциалы и теоремы о дифференцируемых функциях
Приближенное значение функции при , вычисленное с использованием дифференциала первого порядка, равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 5 Тема: Операции над высказываниями
Нулевой
набор у формулы ![]() получается
при следующих значениях переменных …
получается
при следующих значениях переменных …
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
, |
ЗАДАНИЕ N 6 Тема: Неориентированные графы
Для
графа G, изображенного на рисунке,
 матрица
смежности имеет вид …
матрица
смежности имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 7 Тема: Элементы комбинаторики
В урне находятся 5 белых, 7 красных, 6 голубых шаров. Сколько существует способов извлечь 9 шаров так, чтобы среди них оказалось 2 белых, 3 красных и 4 голубых шара?
|
5250 |
ЗАДАНИЕ N 8 Тема: Декартово произведение множеств
Пусть
даны два множества:
![]() ,
, ![]() .
Тогда
геометрическая интерпретация
множества
имеет
вид …
.
Тогда
геометрическая интерпретация
множества
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 9 Тема: Дробно-рациональные функции
Даны
два полинома: ![]() и
и ![]() Тогда
целая часть от деления полинома
Тогда
целая часть от деления полинома ![]() на
полином
на
полином ![]() равна
…
равна
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Выполним
деление заданных полиномов
«уголком»:
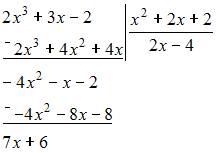 Тогда:
Тогда:
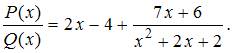 То
есть, целая часть от деления полинома
на
полином
равна
То
есть, целая часть от деления полинома
на
полином
равна ![]()
ЗАДАНИЕ N 10 Тема: Линейные отображения
Прообразом
вектора 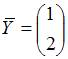 при
линейном преобразовании, заданном
матрицей
при
линейном преобразовании, заданном
матрицей 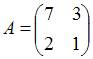 ,
является вектор …
,
является вектор …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 11 Тема: Основные алгебраические структуры
Для
кольца ![]() множество
множество ![]() ,
рассматриваемое с одной алгебраической
операцией сложения, представляет собой
…
,
рассматриваемое с одной алгебраической
операцией сложения, представляет собой
…
|
|
|
абелеву группу |
|
|
|
поле |
|
|
|
целостное кольцо |
|
|
|
область целостности |
ЗАДАНИЕ N 12 Тема: Группы и подгруппы
Подгруппой группы невырожденных матриц по умножению является подмножество матриц с …
|
|
|
единичным определителем |
|
|
|
определителем, равным 2 |
|
|
|
определителем, равным – 1 |
|
|
|
определителями, равными 2 и 0,5 |
ЗАДАНИЕ N 13 Тема: Определение вероятности
Из урны, в которой находятся 6 белых шаров и 4 черных шара, вынимают одновременно 4 шара. Тогда вероятность того, что среди отобранных 3 шара будут белыми, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 14 Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная
случайная величина
задана
законом распределения вероятностей:
 Тогда
значения a и b могут
быть равны …
Тогда
значения a и b могут
быть равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 15 Тема: Числовые характеристики случайных величин
Дискретная
случайная величина X задана
законом распределения вероятностей:
 Тогда
ее дисперсия равна …
Тогда
ее дисперсия равна …
|
|
|
7,56 |
|
|
|
3,2 |
|
|
|
3,36 |
|
|
|
6,0 |
ЗАДАНИЕ N 16 Тема: Полная вероятность. Формулы Байеса
В первой урне 5 черных и 6 белых шаров. Во второй урне 3 белых шара и 6 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет черным, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 17 Тема: Дифференциальная геометрия поверхностей
Вектор
нормали ![]() к
прямому геликоиду
к
прямому геликоиду ![]() в
точке
в
точке ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Найдем
частные производные:
; ![]() .
Тогда
.
Тогда ![]() и
и ![]() ,
и вектор нормали будет равен:
,
и вектор нормали будет равен:
 ;
или
;
или ![]() .
.
ЗАДАНИЕ N 18 Тема: Асимптоты кривой
Асимптоты кривой имеют вид …
|
|
|
и |
|
|
|
и |
|
|
|
и |
|
|
|
и |
ЗАДАНИЕ N 19 Тема: Дифференциальная геометрия кривых
Длина дуги кривой при , равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,14 |
Решение:
Длина
дуги кривой вычисляется по формуле:  ,
где
,
где ![]() -
дифференциал дуги. Вычислив
-
дифференциал дуги. Вычислив  ,
получаем
,
получаем ![]() .
Тогда
.
Тогда 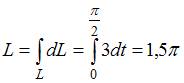 .
.
ЗАДАНИЕ N 20 Тема: Основные понятия топологии
Гомеоморфной к тору является …
|
|
|
«кружка с ручкой» |
|
|
|
сфера |
|
|
|
«крендель» |
|
|
|
куб |
ЗАДАНИЕ N 21 Тема: Интервальные оценки параметров распределения
Точечная оценка среднего квадратического отклонения нормально распределенного количественного признака равна 3,5. Тогда его интервальная оценка может иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Интервальной
оценкой среднего квадратического
отклонения ![]() нормально
распределенного количественного
признака служит доверительный
интервал
нормально
распределенного количественного
признака служит доверительный
интервал
![]() при
при ![]() или
или ![]() при
при ![]() ,
где q находят
по соответствующей таблице приложений.
Этому
определению удовлетворяет интервал
.
,
где q находят
по соответствующей таблице приложений.
Этому
определению удовлетворяет интервал
.
ЗАДАНИЕ N 22 Тема: Проверка статистических гипотез
Правосторонняя критическая область может определяться из соотношения …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 23 Тема: Статистическое распределение выборки
Статистическое
распределение выборки имеет вид
 Тогда
значение относительной частоты
Тогда
значение относительной частоты ![]() равно
…
равно
…
|
|
|
0,25 |
|
|
|
0,05 |
|
|
|
0,26 |
|
|
|
0,75 |
ЗАДАНИЕ N 24 Тема: Элементы корреляционного анализа
Выборочное
уравнение прямой линии регрессии
на
имеет
вид ![]() .
Тогда выборочный коэффициент регрессии
равен …
.
Тогда выборочный коэффициент регрессии
равен …
|
|
|
– 1,5 |
|
|
|
1,5 |
|
|
|
4 |
|
|
|
|
Решение:
Если
выборочное уравнение парной регрессии
имеет вид ![]() ,
то выборочный коэффициент регрессии
равен
,
то выборочный коэффициент регрессии
равен ![]() .
То есть
.
То есть ![]() .
.
ЗАДАНИЕ N 25 Тема: Операции над комплексными числами
Дано комплексное число . Тогда равно …
|
|
|
16 |
|
|
|
|
|
|
|
2 |
|
|
|
|
ЗАДАНИЕ N 26 Тема: Особые точки функции комплексного переменного
Число особых точек функции равно …
|
|
|
3 |
|
|
|
5 |
|
|
|
2 |
|
|
|
1 |
Решение: Для функции точки – полюсы первого порядка, – полюс первого порядка. Следовательно, число особых точек равно трем.
ЗАДАНИЕ N 27 Тема: Дифференцирование функции комплексного переменного
Значение
производной функции ![]() в
точке
в
точке ![]() равно
…
равно
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Производная
функции
имеет
вид 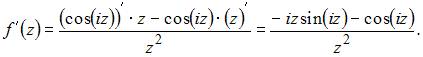 Тогда
Тогда
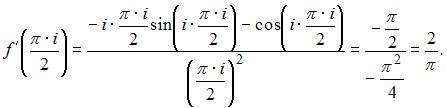
ЗАДАНИЕ N 28 Тема: Области на комплексной плоскости
Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке, удовлетворяют условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Математика i-exam вариант 2
ЗАДАНИЕ N 1 Тема: Плоскость в пространстве
Угол
между плоскостями ![]() и
и ![]() равен
…
равен
…
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 2 Тема: Кривые второго порядка
Радиус
окружности ![]() равен
…
равен
…
|
|
|
2 |
|
|
|
|
|
|
|
4 |
|
|
|
|
Решение:
Окружность
радиуса ![]() с
центром в точке
с
центром в точке ![]() задается
на плоскости уравнением вида
задается
на плоскости уравнением вида ![]() .
Выделим в уравнении
полные
квадраты:
.
Выделим в уравнении
полные
квадраты: ![]() ,
или
,
или ![]() .
Тогда
радиус окружности равен 2.
.
Тогда
радиус окружности равен 2.
ЗАДАНИЕ N 3 Тема: Прямая линия в пространстве
Каноническое
уравнение прямой 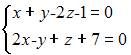 может
иметь вид …
может
иметь вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 4 Тема: Прямоугольные координаты на плоскости
Даны точки и . Тогда координаты точки , симметричной точке относительно точки , равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 5 Тема: Дифференциальные уравнения с разделяющимися переменными
Общее
решение дифференциального уравнения ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 6 Тема: Поле направлений и изоклины
Дано
дифференциальное уравнение ![]() .
Тогда отрезок соответствующего ему
поля направлений в точке
.
Тогда отрезок соответствующего ему
поля направлений в точке ![]() образует
с осью
угол,
равный …
образует
с осью
угол,
равный …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 7 Тема: Задача Коши для дифференциального уравнения первого порядка
Частное
решение дифференциального уравнения ![]() ,
удовлетворяющее условию
,
удовлетворяющее условию ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 8 Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Общее решение системы дифференциальных уравнений имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 9 Тема: Дифференциальное исчисление ФНП
Частная производная функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 10 Тема: Непрерывность функции, точки разрыва
Количество точек разрыва функции равно …
|
|
|
4 |
|
|
|
2 |
|
|
|
1 |
|
|
|
3 |
Решение: Точку называют точкой разрыва функции , если она не является непрерывной в этой точке. В частности, точками разрыва данной функции являются точки, в которых знаменатели равны нулю. То есть , и . Тогда , . Следовательно, получили четыре точки разрыва функции.
ЗАДАНИЕ N 11 Тема: Дифференциалы и теоремы о дифференцируемых функциях
Предел ![]() равен
…
равен
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 12 Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 13 Тема: Асимптоты кривой
Асимптоты
графика кривой 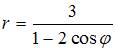 ,
заданной в полярных координатах, имеют
вид …
,
заданной в полярных координатах, имеют
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 14 Тема: Дифференциальная геометрия поверхностей
Вектор
нормали
в
точке ![]() к
поверхности тора
к
поверхности тора 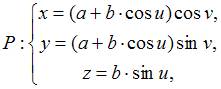 имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Вычислим
частные производные в точке
: ![]() ;
; ![]() ;
Тогда
вектор нормали в точке
;
Тогда
вектор нормали в точке ![]() будет
равен:
будет
равен: 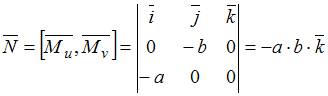 .
.
ЗАДАНИЕ N 15 Тема: Дифференциальная геометрия кривых
Уравнение
нормали к кривой ![]() в
точке
в
точке 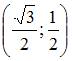 имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 16 Тема: Основные понятия топологии
Внутренностью множества в топологическом пространстве с топологией является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пустое множество |
Решение: Внутренность – это совокупность всех внутренних точек множества, то есть точек из , входящих в с какой-либо своей окрестностью (открытым множеством). Таким образом, внутренностью множества в данном случае является множество .
ЗАДАНИЕ N 17 Тема: Элементы корреляционного анализа
Выборочное
уравнение прямой линии регрессии
на
имеет
вид ![]() .
Тогда выборочный коэффициент корреляции
может быть равен …
.
Тогда выборочный коэффициент корреляции
может быть равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 18 Тема: Интервальные оценки параметров распределения
Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 19 Тема: Проверка статистических гипотез
Левосторонняя критическая область может определяться из соотношения …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 20 Тема: Статистическое распределение выборки
Из
генеральной совокупности извлечена
выборка объема ![]() ,
полигон частот которой имеет вид:
,
полигон частот которой имеет вид:
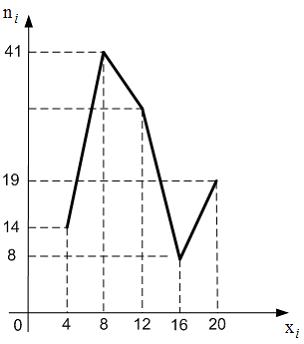 Тогда
число вариант
Тогда
число вариант ![]() в
выборке равно …
в
выборке равно …
|
|
|
32 |
|
|
|
82 |
|
|
|
8 |
|
|
|
31 |
ЗАДАНИЕ N 21 Тема: Операции над высказываниями
Таблица
истинности для формулы ![]() представляет
собой …
представляет
собой …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 22 Тема: Декартово произведение множеств
Декартово
произведение множеств ![]() и
и ![]() представляет
собой …
представляет
собой …
|
|
|
окружность , лежащую в плоскости |
|
|
|
цилиндрическую поверхность |
|
|
|
сферу |
|
|
|
эллиптический
параболоид |
ЗАДАНИЕ N 23 Тема: Элементы комбинаторики
Вокруг костра сидят 12 разбойников. Каждый из них смертельно ненавидит двух ближайших соседей. С целью спрятать награбленное необходимо выделить 5 разбойников. Сколькими способами атаман может назначить пятерых так, чтобы между ними не было распрей?
|
12 |
ЗАДАНИЕ N 24 Тема: Неориентированные графы
Для графа, изображенного на рисунке, последовательность является …
|
|
|
маршрутом |
|
|
|
цепью |
|
|
|
циклом |
|
|
|
деревом |
Решение:
Маршрутом
называют последовательность вершин и
ребер некоторого графа. Маршрут, не
содержащий повторяющихся ребер, называют
цепью. Замкнутая цепь называется циклом.
Деревом называют простой граф, не
содержащий в себе циклов.
Последовательность
не
замкнута, содержит в себе повторяющееся
ребро ![]() ,
включает в себя цикл
,
включает в себя цикл ![]() .
Поэтому она не является, ни «цепью», ни
«циклом», ни «деревом»; а представляет
собой просто «маршрут».
.
Поэтому она не является, ни «цепью», ни
«циклом», ни «деревом»; а представляет
собой просто «маршрут».
ЗАДАНИЕ N 25 Тема: Полная вероятность. Формулы Байеса
В первой урне 5 черных и 6 белых шаров. Во второй урне 3 белых шара и 6 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет черным, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 26 Тема: Определение вероятности
Из урны, в которой находятся 6 белых шаров и 4 черных шара, вынимают одновременно 4 шара. Тогда вероятность того, что среди отобранных 3 шара будут белыми, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 27 Тема: Законы распределения вероятностей дискретных случайных величин
Дискретная
случайная величина
задана
функцией распределения вероятностей
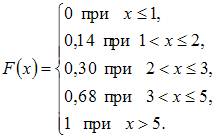 Тогда
вероятность
Тогда
вероятность ![]() равна
…
равна
…
|
|
|
0,54 |
|
|
|
0,38 |
|
|
|
0,70 |
|
|
|
0,86 |
Решение:
Так
как по определению ![]() ,
то случайную величину
можно
задать законом распределения вероятностей
вида
,
то случайную величину
можно
задать законом распределения вероятностей
вида
 Следовательно,
Следовательно, ![]() .
.
ЗАДАНИЕ N 28 Тема: Числовые характеристики случайных величин
Непрерывная случайная величина задана плотностью распределения вероятностей: Тогда ее математическое ожидание равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
ЗАДАНИЕ N 29 Тема: Особые точки функции комплексного переменного
Для функции точка является …
|
|
|
полюсом второго порядка |
|
|
|
полюсом третьего порядка |
|
|
|
полюсом первого порядка |
|
|
|
существенно особой точкой |
ЗАДАНИЕ N 30 Тема: Области на комплексной плоскости
Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке: удовлетворяют условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 31 Тема: Операции над комплексными числами
Если и – корни квадратного уравнения , то равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Решение
квадратного уравнения ![]() находится
по формуле
находится
по формуле 
![]() ,
где под
,
где под ![]() понимаются
все значения корня из комплексного
числа
.
В нашем случае
понимаются
все значения корня из комплексного
числа
.
В нашем случае ![]() и
и ![]() .
Тогда
.
Тогда ![]() .
Решение
можно найти и по теореме Виета. Так
как
.
Решение
можно найти и по теореме Виета. Так
как ![]() ,
то в нашем случае получим, что
,
то в нашем случае получим, что ![]() .
.
ЗАДАНИЕ N 32 Тема: Дифференцирование функции комплексного переменного
Если и , то мнимая часть производной этой функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Производная
функции
равна 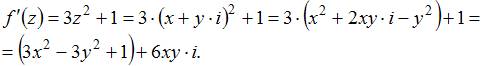 Тогда
Тогда ![]() .
.
ЗАДАНИЕ N 33 Тема: Мера плоского множества
Мера плоского множества равна …
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
ЗАДАНИЕ N 34 Тема: Элементы теории множеств
Даны
два множества: ![]() и
и ![]() .
Тогда количество целых значений
,
принадлежащих пересечению множеств
и
,
равно …
.
Тогда количество целых значений
,
принадлежащих пересечению множеств
и
,
равно …
|
4 |
ЗАДАНИЕ N 35 Тема: Отображение множеств
Прообразом
множества ![]() при
отображении
при
отображении ![]() является
…
является
…
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 36 Тема: Метрические пространства
Расстояние между точками и в метрике , где и , равно …
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
0 |
Решение: .
ЗАДАНИЕ N 37 Тема: Основные алгебраические структуры
В кольце квадратных матриц второго порядка единичный элемент …
|
|
|
– это
матрица |
|
|
|
– это
матрица |
|
|
|
– это
матрица |
|
|
|
не существует |
ЗАДАНИЕ N 38 Тема: Группы и подгруппы
Подгруппой группы целых чисел с введенной операцией сложения является множество …
|
|
|
четных целых чисел |
|
|
|
нечетных целых чисел |
|
|
|
натуральных чисел |
|
|
|
натуральных чисел с нулем |
ЗАДАНИЕ N 39 Тема: Дробно-рациональные функции
Даны два полинома: и Тогда целая часть от деления полинома на полином равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Выполним деление заданных полиномов «уголком»: Тогда: То есть, целая часть от деления полинома на полином равна
ЗАДАНИЕ N 40 Тема: Линейные отображения
Линейный
оператор
отображает
базис ![]() в
векторы:
в
векторы:
![]() ;
; ![]() ;
; ![]() .
Тогда матрица оператора
в
этом базисе имеет вид …
.
Тогда матрица оператора
в
этом базисе имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
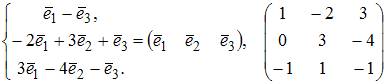
Математика i-exam вариант 1
ЗАДАНИЕ N 1 Тема: Проверка статистических гипотез
Соотношением вида можно определить …
|
|
|
правостороннюю критическую область |
|
|
|
левостороннюю критическую область |
|
|
|
двустороннюю критическую область |
|
|
|
область принятия гипотезы |
ЗАДАНИЕ N 2 Тема: Элементы корреляционного анализа
При построении выборочного уравнения парной регрессии вычислены выборочный коэффициент корреляции и выборочные средние квадратические отклонения . Тогда выборочный коэффициент регрессии на равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 3 Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема , гистограмма частот которой имеет вид: Тогда значение a равно …
|
|
|
38 |
|
|
|
39 |
|
|
|
76 |
|
|
|
37 |
ЗАДАНИЕ N 4 Тема: Интервальные оценки параметров распределения
Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала , где точечная оценка математического ожидания , а точность оценки . В случае уменьшения объема выборки точность оценки ухудшается, то есть значение будет больше 2,13.
ЗАДАНИЕ N 5 Тема: Операции над высказываниями
Из трех логических выражений: эквивалентными являются …
|
|
|
и |
|
|
|
и |
|
|
|
и |
|
|
|
все функции |
ЗАДАНИЕ N 6 Тема: Элементы комбинаторики
Из города в город ведут 5 дорог, из в – 3 дороги, имеются также 2 дороги из в , минуя . Из в можно попасть ____ способом(-ами).
|
17 | |
Решение: Из города в город можно попасть способами, из в – с помощью способов. Тогда из в через можно попасть способами (по правилу произведения); а из в , минуя , можно попасть способами. Поэтому по правилу суммы общее число способов, которыми можно попасть из города в город , равно: .
ЗАДАНИЕ N 7 Тема: Декартово произведение множеств
Пусть заданы два множества: , . Тогда геометрическая интерпретация множества имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 8 Тема: Неориентированные графы
Эйлеровым является граф …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 9 Тема: Дифференциальная геометрия кривых
Траектория движущейся точки задается уравнением Тогда значение касательного ускорения в момент равно …
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
Решение: Касательное ускорение на параметрически заданной кривой вычисляется как . Вычислим производные первого и второго порядка. Найдем , при любых значениях .
ЗАДАНИЕ N 10 Тема: Дифференциальная геометрия поверхностей
Точка с координатами на поверхности является …
|
|
|
гиперболической точкой |
|
|
|
параболической точкой |
|
|
|
эллиптической точкой |
|
|
|
точкой уплощения |
Решение: Тип точки на поверхности определяется по виду соприкасающегося параболоида в этой точке к поверхности. Построим соприкасающийся параболоид: . Вычислим частные производные второго порядка: ; ; . В точке ; ; . Тогда соприкасающийся параболоид является гиперболическим параболоидом, а сама точка относится к гиперболическому типу.
ЗАДАНИЕ N 11 Тема: Асимптоты кривой
Асимптоты кривой имеют вид …
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
и |
Решение: Кривая описывается соотношением , то есть функция представлена в явном виде. В точке функция имеет разрыв, поэтому уравнение вертикальной асимптоты имеет вид: . Наклонные или горизонтальные асимптоты определяются уравнением (для горизонтальных асимптот ). 1. Находим асимптоту при (правую асимптоту): , . Следовательно, уравнение правой асимптоты имеет вид: . 2. Аналогично находим асимптоту при (левую асимптоту): , . Следовательно, уравнение левой асимптоты совпадает с уравнением правой асимптоты и имеет вид: . Таким образом, прямые и являются асимптотами заданной кривой.
ЗАДАНИЕ N 12 Тема: Основные понятия топологии
Внешностью множества в топологическом пространстве с топологией является …
|
|
|
пустое множество |
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Внешность M – это совокупность всех внутренних точек дополнения к множеству M, то есть входящих в дополнение к M с какой-либо своей окрестностью (открытым множеством). Дополнением является множество – закрытое множество, которое не содержит в себе ни одного открытого множества из данной топологии. Таким образом, внешностью множества в данном случае будет пустое множество.
ЗАДАНИЕ N 13 Тема: Непрерывность функции, точки разрыва
Для функции точка является точкой …
|
|
|
разрыва второго рода |
|
|
|
разрыва первого рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
ЗАДАНИЕ N 14 Тема: Дифференциалы и теоремы о дифференцируемых функциях
Приближенное значение функции при , вычисленное с использованием дифференциала первого порядка, равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 15 Тема: Дифференциальное исчисление ФНП
Частная производная функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 16 Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 17 Тема: Поле направлений и изоклины
Поле направлений дифференциального уравнения определяется неравенством …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Так как поле направлений дифференциального уравнения задано в области определения функции двух переменных , то для нахождения области задания поля направлений следует решить неравенство . Тогда .
ЗАДАНИЕ N 18 Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Общее решение системы дифференциальных уравнений имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 19 Тема: Задача Коши для дифференциального уравнения первого порядка
Функция является общим решением дифференциального уравнения 1-го порядка. Тогда для начального условия частное решение этого уравнения имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 20 Тема: Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение будет уравнением с разделяющимися переменными при значении , равном …
|
|
|
2 |
|
|
|
0 |
|
|
|
4 |
|
|
|
1 |
Решение: Данное уравнение можно представить в виде . Это уравнение будет уравнением с разделяющимися переменными при , то есть при . Откуда .
ЗАДАНИЕ N 21 Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков не меньше девяти, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Решение: Для вычисления события (сумма выпавших очков будет не меньше девяти) воспользуемся формулой , где – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае возможны элементарных исходов испытания, из которых благоприятствующими являются исходы вида , , , , , , , и , то есть . Следовательно, .
ЗАДАНИЕ N 22 Тема: Числовые характеристики случайных величин
Непрерывная случайная величина задана плотностью распределения вероятностей: Тогда ее математическое ожидание равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
ЗАДАНИЕ N 23 Тема: Законы распределения вероятностей дискретных случайных величин
Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна …
|
|
|
0,0081 |
|
|
|
0,081 |
|
|
|
0,06 |
|
|
|
0,0729 |
ЗАДАНИЕ N 24 Тема: Полная вероятность. Формулы Байеса
Имеются четыре урны, содержащие по 3 белых и 7 черных шаров, и шесть урн, содержащих по 8 белых и 2 черных шара. Из наудачу взятой урны вытаскивается один шар, который оказался белым. Тогда вероятность того, что этот шар был вынут из первой серии урн, равна …
|
|
|
0,20 |
|
|
|
0,80 |
|
|
|
0,72 |
|
|
|
0,40 |
Решение: Предварительно вычислим вероятность события A (вынутый наудачу шар – белый) по формуле полной вероятности: . Здесь – вероятность того, что шар извлечен из первой серии урн; – вероятность того, что шар извлечен из второй серии урн; – условная вероятность того, что вынутый шар белый, если из он извлечен из первой серии урн; – условная вероятность того, что вынутый шар белый, если из он извлечен из второй серии урн. Тогда . Теперь вычислим условную вероятность того, что этот шар был извлечен из первой серии урн, по формуле Байеса: .
ЗАДАНИЕ N 25 Тема: Мера плоского множества
Мера плоского множества равна …
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
ЗАДАНИЕ N 26 Тема: Метрические пространства
Расстояние между точками и в метрике , где и , равно …
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
0 |
Решение: .
ЗАДАНИЕ N 27 Тема: Элементы теории множеств
Даны три множества: , и . Тогда число элементов множества равно …
|
1 | |
Решение: Определим множество и выполним операцию пересечения . В результате получится множество , состоящее из одного элемента.
ЗАДАНИЕ N 28 Тема: Отображение множеств
Пусть задано отображение . Тогда представляет собой …
|
|
|
единичную окружность |
|
|
|
отрезок |
|
|
|
квадрат |
|
|
|
гиперболу |
ЗАДАНИЕ N 29 Тема: Линейные отображения
Пусть – базис пространства . Операторы и этого пространства заданы матрицами ; . Тогда матрица оператора равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: .
ЗАДАНИЕ N 30 Тема: Основные алгебраические структуры
Обратным элементом для матрицы относительно операции сложения матриц является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 31 Тема: Дробно-рациональные функции
Множество всех дробно-рациональных функций образует поле относительно обычных операций сложения и умножения таких функций. Пусть и , причем и Тогда числитель суммы равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Разложим на линейные множители знаменатели дробно-рациональных функций и : Тогда То есть, числитель суммы равен .
ЗАДАНИЕ N 32 Тема: Группы и подгруппы
На множестве целых чисел группу образует операция * определенная как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 33 Тема: Кривые второго порядка
Уравнение директрисы параболы, проходящей через точки , и симметричной относительно оси , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Каноническое уравнение параболы, проходящей через начало координат и симметричной относительно оси имеет вид: , а уравнение директрисы: . Параметр находится из условия, что точка принадлежит параболе, то есть , . Тогда уравнение директрисы параболы примет вид: .
ЗАДАНИЕ N 34 Тема: Прямоугольные координаты на плоскости
Точки и лежат на одной прямой, параллельной оси ординат. Расстояние между точками и равно 6. Тогда положительные координаты точки равны …
|
|
|
, |
|
|
|
, |
|
|
|
, |
|
|
|
, |
Решение: Точки, лежащие на одной прямой, параллельной оси OY, имеют одинаковые абсциссы, следовательно, и . Расстояние между двумя точками и находится по формуле . Тогда расстояние между точками и можно найти как . Из условия , получаем , или . Следовательно, ; . Тогда положительные координаты точки равны: , .
ЗАДАНИЕ N 35 Тема: Плоскость в пространстве
Уравнение плоскости, проходящей через точку параллельно векторам и , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Уравнение плоскости, проходящей через точку с нормальным вектором , имеет вид: . В качестве нормального вектора плоскости возьмем векторное произведение векторов и . Тогда , или . Подставляя в уравнение плоскости координаты точки и вектора , получим: или .
ЗАДАНИЕ N 36 Тема: Прямая линия в пространстве
Острый угол между прямыми и равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Угол между прямыми и определяется как угол между их направляющими векторами: и , который можно вычислить по формуле: . Тогда , то есть .
ЗАДАНИЕ N 37 Тема: Особые точки функции комплексного переменного
Число особых точек функции равно …
|
|
|
3 |
|
|
|
5 |
|
|
|
2 |
|
|
|
1 |
Решение: Для функции точки – полюсы первого порядка, – полюс первого порядка. Следовательно, число особых точек равно трем.
ЗАДАНИЕ N 38 Тема: Дифференцирование функции комплексного переменного
Если и , то мнимая часть производной этой функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 39 Тема: Области на комплексной плоскости
Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке, удовлетворяют условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 40 Тема: Операции над комплексными числами
Дано комплексное число . Тогда равно …
|
|
|
16 |
|
|
|
|
|
|
|
2 |
|
|
|
|
Решение: Если комплексное число в тригонометрической форме имеет вид , то по формуле Муавра , где – натуральное число. Запишем число в тригонометрической форме: 1) находим модуль числа ; 2) составляем систему уравнений для нахождения аргумента и главного значения аргумента: 3) находим главное значение аргумента комплексного числа , которое равно ; 4) тогда . Следовательно,
Математика i-exam вариант 1
ЗАДАНИЕ N 1 Тема: Проверка статистических гипотез
Соотношением вида можно определить …
|
|
|
правостороннюю критическую область |
|
|
|
левостороннюю критическую область |
|
|
|
двустороннюю критическую область |
|
|
|
область принятия гипотезы |
ЗАДАНИЕ N 2 Тема: Элементы корреляционного анализа
При построении выборочного уравнения парной регрессии вычислены выборочный коэффициент корреляции и выборочные средние квадратические отклонения . Тогда выборочный коэффициент регрессии на равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 3 Тема: Статистическое распределение выборки
Из генеральной совокупности извлечена выборка объема , гистограмма частот которой имеет вид: Тогда значение a равно …
|
|
|
38 |
|
|
|
39 |
|
|
|
76 |
|
|
|
37 |
ЗАДАНИЕ N 4 Тема: Интервальные оценки параметров распределения
Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Доверительный интервал для оценки математического ожидания нормально распределенного количественного признака можно представить в виде симметричного интервала , где точечная оценка математического ожидания , а точность оценки . В случае уменьшения объема выборки точность оценки ухудшается, то есть значение будет больше 2,13.
ЗАДАНИЕ N 5 Тема: Операции над высказываниями
Из трех логических выражений: эквивалентными являются …
|
|
|
и |
|
|
|
и |
|
|
|
и |
|
|
|
все функции |
ЗАДАНИЕ N 6 Тема: Элементы комбинаторики
Из города в город ведут 5 дорог, из в – 3 дороги, имеются также 2 дороги из в , минуя . Из в можно попасть ____ способом(-ами).
|
17 | |
Решение: Из города в город можно попасть способами, из в – с помощью способов. Тогда из в через можно попасть способами (по правилу произведения); а из в , минуя , можно попасть способами. Поэтому по правилу суммы общее число способов, которыми можно попасть из города в город , равно: .
ЗАДАНИЕ N 7 Тема: Декартово произведение множеств
Пусть заданы два множества: , . Тогда геометрическая интерпретация множества имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 8 Тема: Неориентированные графы
Эйлеровым является граф …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 9 Тема: Дифференциальная геометрия кривых
Траектория движущейся точки задается уравнением Тогда значение касательного ускорения в момент равно …
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
Решение: Касательное ускорение на параметрически заданной кривой вычисляется как . Вычислим производные первого и второго порядка. Найдем , при любых значениях .
ЗАДАНИЕ N 10 Тема: Дифференциальная геометрия поверхностей
Точка с координатами на поверхности является …
|
|
|
гиперболической точкой |
|
|
|
параболической точкой |
|
|
|
эллиптической точкой |
|
|
|
точкой уплощения |
Решение: Тип точки на поверхности определяется по виду соприкасающегося параболоида в этой точке к поверхности. Построим соприкасающийся параболоид: . Вычислим частные производные второго порядка: ; ; . В точке ; ; . Тогда соприкасающийся параболоид является гиперболическим параболоидом, а сама точка относится к гиперболическому типу.
ЗАДАНИЕ N 11 Тема: Асимптоты кривой
Асимптоты кривой имеют вид …
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
и |
Решение: Кривая описывается соотношением , то есть функция представлена в явном виде. В точке функция имеет разрыв, поэтому уравнение вертикальной асимптоты имеет вид: . Наклонные или горизонтальные асимптоты определяются уравнением (для горизонтальных асимптот ). 1. Находим асимптоту при (правую асимптоту): , . Следовательно, уравнение правой асимптоты имеет вид: . 2. Аналогично находим асимптоту при (левую асимптоту): , . Следовательно, уравнение левой асимптоты совпадает с уравнением правой асимптоты и имеет вид: . Таким образом, прямые и являются асимптотами заданной кривой.
ЗАДАНИЕ N 12 Тема: Основные понятия топологии
Внешностью множества в топологическом пространстве с топологией является …
|
|
|
пустое множество |
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Внешность M – это совокупность всех внутренних точек дополнения к множеству M, то есть входящих в дополнение к M с какой-либо своей окрестностью (открытым множеством). Дополнением является множество – закрытое множество, которое не содержит в себе ни одного открытого множества из данной топологии. Таким образом, внешностью множества в данном случае будет пустое множество.
ЗАДАНИЕ N 13 Тема: Непрерывность функции, точки разрыва
Для функции точка является точкой …
|
|
|
разрыва второго рода |
|
|
|
разрыва первого рода |
|
|
|
непрерывности |
|
|
|
устранимого разрыва |
ЗАДАНИЕ N 14 Тема: Дифференциалы и теоремы о дифференцируемых функциях
Приближенное значение функции при , вычисленное с использованием дифференциала первого порядка, равно …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 15 Тема: Дифференциальное исчисление ФНП
Частная производная функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 16 Тема: Приложения определенного интеграла
Площадь фигуры, изображенной на рисунке равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 17 Тема: Поле направлений и изоклины
Поле направлений дифференциального уравнения определяется неравенством …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Так как поле направлений дифференциального уравнения задано в области определения функции двух переменных , то для нахождения области задания поля направлений следует решить неравенство . Тогда .
ЗАДАНИЕ N 18 Тема: Системы двух линейных дифференциальных уравнений с постоянными коэффициентами
Общее решение системы дифференциальных уравнений имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 19 Тема: Задача Коши для дифференциального уравнения первого порядка
Функция является общим решением дифференциального уравнения 1-го порядка. Тогда для начального условия частное решение этого уравнения имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 20 Тема: Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение будет уравнением с разделяющимися переменными при значении , равном …
|
|
|
2 |
|
|
|
0 |
|
|
|
4 |
|
|
|
1 |
Решение: Данное уравнение можно представить в виде . Это уравнение будет уравнением с разделяющимися переменными при , то есть при . Откуда .
ЗАДАНИЕ N 21 Тема: Определение вероятности
Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков не меньше девяти, равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
Решение: Для вычисления события (сумма выпавших очков будет не меньше девяти) воспользуемся формулой , где – общее число возможных элементарных исходов испытания, а m – число элементарных исходов, благоприятствующих появлению события A. В нашем случае возможны элементарных исходов испытания, из которых благоприятствующими являются исходы вида , , , , , , , и , то есть . Следовательно, .
ЗАДАНИЕ N 22 Тема: Числовые характеристики случайных величин
Непрерывная случайная величина задана плотностью распределения вероятностей: Тогда ее математическое ожидание равно …
|
|
|
3 |
|
|
|
2 |
|
|
|
1 |
|
|
|
0 |
ЗАДАНИЕ N 23 Тема: Законы распределения вероятностей дискретных случайных величин
Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна …
|
|
|
0,0081 |
|
|
|
0,081 |
|
|
|
0,06 |
|
|
|
0,0729 |
ЗАДАНИЕ N 24 Тема: Полная вероятность. Формулы Байеса
Имеются четыре урны, содержащие по 3 белых и 7 черных шаров, и шесть урн, содержащих по 8 белых и 2 черных шара. Из наудачу взятой урны вытаскивается один шар, который оказался белым. Тогда вероятность того, что этот шар был вынут из первой серии урн, равна …
|
|
|
0,20 |
|
|
|
0,80 |
|
|
|
0,72 |
|
|
|
0,40 |
Решение: Предварительно вычислим вероятность события A (вынутый наудачу шар – белый) по формуле полной вероятности: . Здесь – вероятность того, что шар извлечен из первой серии урн; – вероятность того, что шар извлечен из второй серии урн; – условная вероятность того, что вынутый шар белый, если из он извлечен из первой серии урн; – условная вероятность того, что вынутый шар белый, если из он извлечен из второй серии урн. Тогда . Теперь вычислим условную вероятность того, что этот шар был извлечен из первой серии урн, по формуле Байеса: .
ЗАДАНИЕ N 25 Тема: Мера плоского множества
Мера плоского множества равна …
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
ЗАДАНИЕ N 26 Тема: Метрические пространства
Расстояние между точками и в метрике , где и , равно …
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
0 |
Решение: .
ЗАДАНИЕ N 27 Тема: Элементы теории множеств
Даны три множества: , и . Тогда число элементов множества равно …
|
1 | |
Решение: Определим множество и выполним операцию пересечения . В результате получится множество , состоящее из одного элемента.
ЗАДАНИЕ N 28 Тема: Отображение множеств
Пусть задано отображение . Тогда представляет собой …
|
|
|
единичную окружность |
|
|
|
отрезок |
|
|
|
квадрат |
|
|
|
гиперболу |
ЗАДАНИЕ N 29 Тема: Линейные отображения
Пусть – базис пространства . Операторы и этого пространства заданы матрицами ; . Тогда матрица оператора равна …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: .
ЗАДАНИЕ N 30 Тема: Основные алгебраические структуры
Обратным элементом для матрицы относительно операции сложения матриц является …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 31 Тема: Дробно-рациональные функции
Множество всех дробно-рациональных функций образует поле относительно обычных операций сложения и умножения таких функций. Пусть и , причем и Тогда числитель суммы равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Разложим на линейные множители знаменатели дробно-рациональных функций и : Тогда То есть, числитель суммы равен .
ЗАДАНИЕ N 32 Тема: Группы и подгруппы
На множестве целых чисел группу образует операция * определенная как …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 33 Тема: Кривые второго порядка
Уравнение директрисы параболы, проходящей через точки , и симметричной относительно оси , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Каноническое уравнение параболы, проходящей через начало координат и симметричной относительно оси имеет вид: , а уравнение директрисы: . Параметр находится из условия, что точка принадлежит параболе, то есть , . Тогда уравнение директрисы параболы примет вид: .
ЗАДАНИЕ N 34 Тема: Прямоугольные координаты на плоскости
Точки и лежат на одной прямой, параллельной оси ординат. Расстояние между точками и равно 6. Тогда положительные координаты точки равны …
|
|
|
, |
|
|
|
, |
|
|
|
, |
|
|
|
, |
Решение: Точки, лежащие на одной прямой, параллельной оси OY, имеют одинаковые абсциссы, следовательно, и . Расстояние между двумя точками и находится по формуле . Тогда расстояние между точками и можно найти как . Из условия , получаем , или . Следовательно, ; . Тогда положительные координаты точки равны: , .
ЗАДАНИЕ N 35 Тема: Плоскость в пространстве
Уравнение плоскости, проходящей через точку параллельно векторам и , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Уравнение плоскости, проходящей через точку с нормальным вектором , имеет вид: . В качестве нормального вектора плоскости возьмем векторное произведение векторов и . Тогда , или . Подставляя в уравнение плоскости координаты точки и вектора , получим: или .
ЗАДАНИЕ N 36 Тема: Прямая линия в пространстве
Острый угол между прямыми и равен …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Угол между прямыми и определяется как угол между их направляющими векторами: и , который можно вычислить по формуле: . Тогда , то есть .
ЗАДАНИЕ N 37 Тема: Особые точки функции комплексного переменного
Число особых точек функции равно …
|
|
|
3 |
|
|
|
5 |
|
|
|
2 |
|
|
|
1 |
Решение: Для функции точки – полюсы первого порядка, – полюс первого порядка. Следовательно, число особых точек равно трем.
ЗАДАНИЕ N 38 Тема: Дифференцирование функции комплексного переменного
Если и , то мнимая часть производной этой функции имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 39 Тема: Области на комплексной плоскости
Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке, удовлетворяют условию …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ЗАДАНИЕ N 40 Тема: Операции над комплексными числами
Дано комплексное число . Тогда равно …
|
|
|
16 |
|
|
|
|
|
|
|
2 |
|
|
|
|
Решение: Если комплексное число в тригонометрической форме имеет вид , то по формуле Муавра , где – натуральное число. Запишем число в тригонометрической форме: 1) находим модуль числа ; 2) составляем систему уравнений для нахождения аргумента и главного значения аргумента: 3) находим главное значение аргумента комплексного числа , которое равно ; 4) тогда . Следовательно,
ДЕ1.Абстрактная алгебра
1)Тема: Группы и подгруппы Группу по сложению образует множество …
|
целых чисел |
натуральных чисел |
|
натуральных чисел с нулем |
|
действительных чисел без нуля |
|
2)Тема: Дробно-рациональные функции
Разложение дробно-рациональной функции на простые дроби над полем вещественных чисел имеет вид …
Решение: 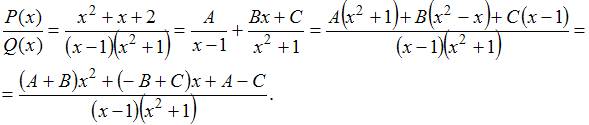
Получаем
систему трех уравнений с тремя
неизвестными: 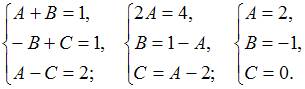
Тогда 
3)Тема: Основные алгебраические структуры В кольце квадратных матриц второго порядка единичный элемент … – это матрица
4)Тема: Линейные отображения
Пусть
базис
пространства
Операторы![]() и
и![]() этого
пространства заданы матрицами
.
Тогда матрица оператора
равна
этого
пространства заданы матрицами
.
Тогда матрица оператора
равна
Решение:
Тема: Дробно-рациональные функции Разложение дробно-рациональной функции на простые дроби над полем вещественных чисел имеет вид …
Тема: Линейные отображения Линейный оператор отображает базис в векторы: Тогда матрица оператора в этом базисе имеет вид …
Решение:
Тема: Основные алгебраические структуры В кольце целых четных чисел единичный элемент …
|
не существует |
Решение: В кольце целых четных чисел единичный элемент не существует.
Тема: Группы и подгруппы Группу по умножению образует множество …
|
действительных чисел без нуля |
действительных чисел |
|
целых чисел |
|
натуральных чисел с нулем |
|
Решение: Группу образует множество действительных чисел без нуля с введенной операцией умножения чисел. Все остальные множества групп не образуют, так как, например, нуль не имеет обратного элемента.
Тема: Группы и подгруппы Операция «+» – сложения образует группу на множестве …
|
целых четных чисел |
натуральных чисел |
|
целых нечетных чисел |
|
действительных чисел без нуля |
|
Решение: Множество целых четных чисел с введенной операцией сложения образует группу. Множество натуральных чисел не группа, так как, например, не имеет противоположного элемента. Множество целых нечетных не имеет нулевого элемента, как и множество действительных чисел без нуля.
Тема:
Линейные отображения
Из
заданных операторов пространства ![]() –
пространства трехмерных векторов,
линейным является оператор …
–
пространства трехмерных векторов,
линейным является оператор …![]()
Тема: Основные алгебраические структуры В кольце целых четных чисел единичный элемент …
|
не существует |
равен |
|
равен |
|
равен |
|
Решение: В кольце целых четных чисел единичный элемент не существует.
Тема:
Основные алгебраические структуры
Подалгеброй
алгебры ![]() является
совокупность …
является
совокупность …
|
|
|
|
|
|
|
|
Решение:
Совокупности ![]() и
не
являются подалгебрами алгебры
,
так как,
и
не
являются подалгебрами алгебры
,
так как, ![]() .
Совокупность
.
Совокупность ![]() не
является подалгеброй алгебры
,
так как множество
не
является подалгеброй алгебры
,
так как множество ![]() не
замкнуто относительно
умножения.
Совокупность
является
подалгеброй алгебры
,
так как
не
замкнуто относительно
умножения.
Совокупность
является
подалгеброй алгебры
,
так как ![]() и
множество
и
множество![]() замкнуто
относительно умножения.
замкнуто
относительно умножения.
Тема: Группы и подгруппы Подгруппой группы целых чисел с введенной операцией сложения является множество …
|
четных целых чисел |
нечетных целых чисел |
|
натуральных чисел |
|
натуральных чисел с нулем |
|
Тема:
Дробно-рациональные функции
Множество
всех дробно-рациональных функций
образует поле
относительно
обычных операций сложения и умножения
таких функций.
Пусть
и
,
причем 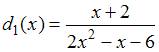 и
и 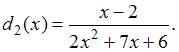 Тогда
числитель произведения
Тогда
числитель произведения ![]() равен
…
равен
…
|
1 |
|
|
|
|
|
|
Решение:
Разложим
на линейные множители знаменатели
дробно-рациональных функций
и
:
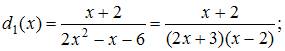
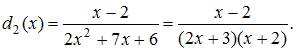 Тогда
Тогда 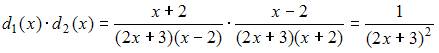 .
То
есть числитель произведения
равен
1.
.
То
есть числитель произведения
равен
1.
Тема:
Дробно-рациональные функции
Разложение
дробно-рациональной функции 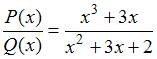 на
элементарные дроби имеет вид …
на
элементарные дроби имеет вид …
|
|
|
|
|
|
|
|
Решение:
Выполним
деление заданных полиномов
«уголком»:
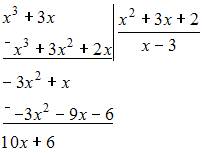 Разложим
знаменатель на простые множители:
Разложим
знаменатель на простые множители: ![]() .
Тогда
.
Тогда
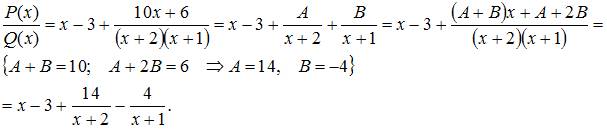
Тема: Группы и подгруппы Группу по умножению образует множество …
|
действительных чисел без нуля |
действительных чисел |
|
целых чисел |
|
натуральных чисел с нулем |
|
Решение: Группу образует множество действительных чисел без нуля с введенной операцией умножения чисел. Все остальные множества групп не образуют, так как, например, нуль не имеет обратного элемента.
Тема: Линейные отображения Из заданных операторов пространства – пространства трехмерных векторов, линейным является оператор …
|
|
|
|
|
|
|
|
Решение:
Линейным
называется отображение
удовлетворяющее
условиям:
,
.
Проверим
на линейность оператор ![]() :
:
![]() ,
,
![]() ,
Следовательно
-
первое условие не выполнено, а значит
не
является линейным оператором.
Для
оператора
,
Следовательно
-
первое условие не выполнено, а значит
не
является линейным оператором.
Для
оператора ![]() проверим
выполнение второго условия:
проверим
выполнение второго условия:
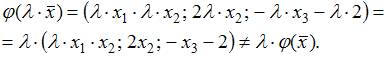 Условие
не выполняется, значит
не
линейный оператор.
Проверим выполнение
второго условия для оператора
Условие
не выполняется, значит
не
линейный оператор.
Проверим выполнение
второго условия для оператора ![]() :
:
![]() Следовательно,
данный оператор не является
линейным.
Проверим выполнение условий
линейности для оператора
Следовательно,
данный оператор не является
линейным.
Проверим выполнение условий
линейности для оператора ![]() :
:
![]() ,
,
![]() ,
Следовательно
–
первое условие выполнено.
,
Следовательно
–
первое условие выполнено.
![]() –
второе условие выполнено. Поэтому
является
линейным оператором.
–
второе условие выполнено. Поэтому
является
линейным оператором.
Тема:
Основные алгебраические структуры
Подалгеброй
алгебры ![]() является
совокупность …
является
совокупность …
|
|
|
|
|
|
|
|
Решение:
Подалгеброй
алгебры ![]() ,
называют совокупность
,
называют совокупность ![]() ,
где
,
где ![]() ,
причем
,
причем ![]() замкнуто
относительно всех операций из
замкнуто
относительно всех операций из ![]() не
является подалгеброй алгебры
,
так как
не
является подалгеброй алгебры
,
так как ![]() и
не
являются подалгебрами алгебры
,
так как, не совпадают множества заданных
операций.
является
подалгеброй алгебры
,
так как
и
не
являются подалгебрами алгебры
,
так как, не совпадают множества заданных
операций.
является
подалгеброй алгебры
,
так как ![]() и
каждая главная операция является
ограничением соответствующей операции
на
и
каждая главная операция является
ограничением соответствующей операции
на ![]()
Тема:
Основные алгебраические структуры
![]() является
подалгеброй алгебры …
является
подалгеброй алгебры …
|
|
|
|
|
|
|
|
Решение:
является
подалгеброй алгебры
,
так как ![]() и
каждая главная операция является
ограничением соответствующей операции
на
и
каждая главная операция является
ограничением соответствующей операции
на ![]() .
.
Тема: Дробно-рациональные функции Разложение дробно-рациональной функции на элементарные дроби имеет вид
Тема:
Линейные отображения
Образом
вектора 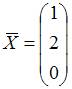 при
линейном преобразовании, заданном
матрицей
при
линейном преобразовании, заданном
матрицей 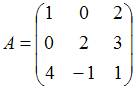 ,
является вектор …
,
является вектор …
|
|
|
|
|
|
|
|
Решение:
Так
как образ ![]() вектора
вектора ![]() определяется
по формуле:
определяется
по формуле: ![]() ,
то
,
то 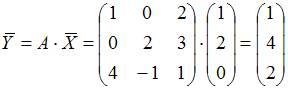 .
.
Тема: Основные алгебраические структуры Подалгеброй алгебры является совокупность …
|
|
|
|
|
|
|
|
Решение: Подалгеброй алгебры , называют совокупность , где , причем замкнуто относительно всех операций из не является подалгеброй алгебры , так как и не являются подалгебрами алгебры , так как, не совпадают множества заданных операций. является подалгеброй алгебры , так как и каждая главная операция является ограничением соответствующей операции на
Тема: Группы и подгруппы Мультипликативная группа рациональных чисел – это множество рациональных чисел …
|
без нуля с операцией умножения |
с операцией сложения |
|
с операцией умножения |
|
без нуля с отношением порядка |
|
Решение: Мультипликативная группа определяется операцией умножения. Поэтому множество рациональных чисел с операцией сложения и множество рациональных чисел без нуля с отношением порядка не являются мультипликативными группами. Множество рациональных чисел с операцией умножения не является группой, так как для элемента 0 нет обратного относительно умножения. Тогда мультипликативная группа рациональных чисел – это множество рациональных чисел без нуля с операцией умножения.
Тема: Дробно-рациональные функции Множество всех дробно-рациональных функций образует поле относительно обычных операций сложения и умножения таких функций. Пусть и , причем и Тогда числитель суммы равен …
|
|
|
|
|
|
|
|
Решение: Разложим на линейные множители знаменатели дробно-рациональных функций и : Тогда То есть, числитель суммы равен .
Тема:
Линейные отображения
Линейное
преобразование
в
базисе ![]() имеет
матрицу
имеет
матрицу 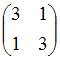 .
Тогда матрица этого оператора в базисе
.
Тогда матрица этого оператора в базисе ![]() ,
где
,
где ![]() ;
; ![]() , имеет
вид …
, имеет
вид …
|
|
|
|
|
|
|
|
Решение:
Матрица
оператора
в
базисе ![]() вычисляется
по формуле
вычисляется
по формуле ![]() ,
где
–
матрица перехода от базиса
к
базису
.
Матрица
перехода
,
где
–
матрица перехода от базиса
к
базису
.
Матрица
перехода 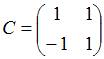 ,
тогда
,
тогда  .
Матрица линейного оператора
.
Матрица линейного оператора 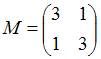 .
Тогда
.
Тогда 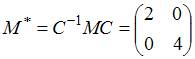 .
.
Тема: Группы и подгруппы Коммутативной группой является множество …
|
квадратных матриц с введенной операцией сложения |
невырожденных квадратных матриц с введенной операцией умножения |
|
натуральных чисел с 0, с введенной операцией сложения |
|
натуральных чисел с введенной операцией сложения |
|
Решение:
Множество
квадратных матриц с введенной операцией
сложения образует группу: ассоциативность
выполняется, нейтральным элементом
группы является нулевая матрица, для
любой матрицы существует
противоположная.
Множество невырожденных
квадратных матриц с введенной операцией
умножения образует группу, но она не
является коммутативной, т.к. не для любых
матриц
и
выполняется
равенство ![]() .
Множество
натуральных чисел (с 0, или без него) с
введенной операцией сложения не является
группой, т.к. нет противоположного
элемента, например, у элемента
.
.
Множество
натуральных чисел (с 0, или без него) с
введенной операцией сложения не является
группой, т.к. нет противоположного
элемента, например, у элемента
.
Тема: Основные алгебраические структуры Для кольца множество , рассматриваемое с одной алгебраической операцией сложения, представляет собой …
|
абелеву группу |
поле |
|
целостное кольцо |
|
область целостности |
|
Решение: Для кольца множество , рассматриваемое с одной алгебраической операцией сложения, представляет собой абелеву группу.
Тема:
Линейные отображения
Дано
линейное преобразование векторов на
плоскости ![]() ,
которое каждый вектор переводит в вектор
той же длины, но противоположно
направленный исходному. Тогда
матрица
этого
преобразования имеет вид …
,
которое каждый вектор переводит в вектор
той же длины, но противоположно
направленный исходному. Тогда
матрица
этого
преобразования имеет вид …
|
|
|
|
|
|
|
|
Решение:
Так
как ![]() и
и ![]() ,
то матрица такого линейного преобразования
имеет вид
,
то матрица такого линейного преобразования
имеет вид 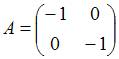 .
.
Тема: Основные алгебраические структуры В кольце квадратных матриц второго порядка единичный элемент …
|
– это матрица |
– это матрица |
|
– это матрица |
|
не существует |
|
Тема:
Дробно-рациональные функции
Даны
два полинома: ![]() и
и ![]() Тогда
целая часть от деления полинома
на
полином
равна
…
Тогда
целая часть от деления полинома
на
полином
равна
…
|
|
|
|
|
|
|
|
Решение:
Выполним
деление заданных полиномов
«уголком»:
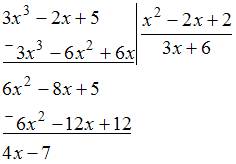 Тогда:
Тогда:
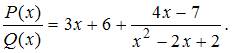 То
есть, целая часть от деления полинома
на
полином
равна
То
есть, целая часть от деления полинома
на
полином
равна ![]()
ема:
Основные алгебраические
структуры
Элемент ![]() называется
обратным к элементу
называется
обратным к элементу ![]() в
группе G с единичным элементом
в
группе G с единичным элементом![]() ,
если …
,
если …
|
|
|
|
|
|
|
|
Тема: Группы и подгруппы Подгруппой группы целых чисел с введенной операцией сложения является множество …
|
четных целых чисел |
нечетных целых чисел |
|
натуральных чисел |
|
натуральных чисел с нулем |
|
Решение: Данное подмножество должно быть замкнуто относительно операций сложения и взятия противоположного элемента. Этим условиям удовлетворяет, например, множество четных целых чисел.
Тема: Линейные отображения Линейным отображением пространства трехмерных векторов на пространство двумерных векторов является …
|
|
|
|
|
|
|
|
Решение: Линейным называется отображение удовлетворяющее условиям: , . Проверим на линейность отображение : , , Следовательно – первое условие не выполнено, а значит не является линейным отображением. Для отображения проверим выполнение второго условия: Условие не выполняется, значит не линейное отображение. Проверим выполнение второго условия для отображения : Следовательно, данное отображение не является линейным. Проверим выполнение условий линейности для отображения : , , Следовательно – первое условие выполнено. – второе условие выполнено. Поэтому является линейным отображением.
ДЕ2.Аналитическая геометрия
Тема:
Прямоугольные координаты на плоскости
Даны
три вершины параллелограмма: ![]() ,
,![]() ,
, ![]() .Тогда
четвертая вершина
.Тогда
четвертая вершина ![]() ,
противолежащая вершине В, имеет
координаты
,
противолежащая вершине В, имеет
координаты ![]() .
.
Решение:
Воспользуемся
формулой деления отрезка пополам.
Координаты точки ![]() ,
делящей отрезок между точками
,
делящей отрезок между точками![]() и
и ![]() пополам,
находятся по формулам:
пополам,
находятся по формулам:  ,
,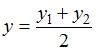 .
Найдем координаты точки М пересечения
диагоналей параллелограмма как координаты
середины отрезка АС (диагонали
параллелограмма точкой пересечения
делятся пополам):
.
Найдем координаты точки М пересечения
диагоналей параллелограмма как координаты
середины отрезка АС (диагонали
параллелограмма точкой пересечения
делятся пополам): 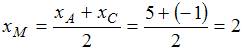 ,
,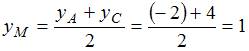 .
Зная координаты точек В и М (как середины
отрезка ВД) найдем координаты точки
.
Зная координаты точек В и М (как середины
отрезка ВД) найдем координаты точки ![]()
![]()
![]() то
есть точка имеет координаты
.
то
есть точка имеет координаты
.
Тема: Прямая линия в пространстве Острый угол между прямыми и равен
Решение: Угол между прямыми определяется как угол между их направляющими векторами: и который можно вычислить по формуле:
тогда
Тема:
Кривые второго порядка
Мнимая
полуось гиперболы ![]() равна
…
равна
…
|
|
|
3 |
Тема:
Плоскость в пространстве
Нормальное
уравнение плоскости ![]() имеет
вид …
имеет
вид …![]()
Тема:
Плоскость в пространстве
Плоскости ![]() и
и ![]() перпендикулярны
при значении
перпендикулярны
при значении ![]() ,
равном
,
равном ![]()
Решение:
Плоскости,
заданные общими уравнениями ![]() и
и ![]() перпендикулярны
при условии, что
перпендикулярны
при условии, что![]() .
Тогда
.
Тогда ![]() то
есть
.
то
есть
.
Тема:
Кривые второго порядка
Расстояние
между фокусами гиперболы 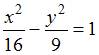 равно
10.
равно
10.
Тема:
Прямая линия в пространстве
Параметрические
уравнения прямой, параллельной оси ![]() и
проходящей через точку
и
проходящей через точку![]() имеют
вид …
имеют
вид …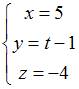
Решение:
Параметрические
уравнения прямой, проходящей через
точку![]() с
направляющим вектором
с
направляющим вектором![]() имеют
вид
имеют
вид 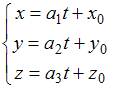 .За
направляющий вектор прямой можно взять
.За
направляющий вектор прямой можно взять ![]()
Тогда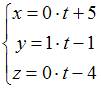 или
или
Тема:
Прямоугольные координаты на
плоскости
Точка ![]() лежит
на оси абсцисс и равноудалена от точки
лежит
на оси абсцисс и равноудалена от точки ![]() и
начала координат. Тогда точка
и
начала координат. Тогда точка ![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Так
как точка
лежит
на оси абсцисс, то ее ордината ![]() .
Так как точка
.
Так как точка ![]() равноудалена
от точки
и
начала координат
равноудалена
от точки
и
начала координат![]() ,
то расстояния от точки
до
точек
и
равны.
Тогда
,
то расстояния от точки
до
точек
и
равны.
Тогда ![]() или
или
![]()
![]() ,
т.е.
,
т.е. ![]()
Тема:
Плоскость в пространстве
Общее
уравнение плоскости, проходящей через
точку ![]() перпендикулярно
прямой
перпендикулярно
прямой ![]() имеет
вид …
имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Уравнение
плоскости, проходящей через точку ![]() с
нормальным вектором
с
нормальным вектором ![]() ,
имеет вид:
,
имеет вид: ![]() .
Так
как эта плоскость перпендикулярна
прямой
,
то в качестве нормального вектора
плоскости можно использовать направляющий
вектор этой прямой, то есть
.
Так
как эта плоскость перпендикулярна
прямой
,
то в качестве нормального вектора
плоскости можно использовать направляющий
вектор этой прямой, то есть ![]() .
Тогда
.
Тогда
![]() или
.
или
.
Тема: Кривые второго порядка Асимптоты гиперболы задаются уравнениями …
|
|
|
|
Решение: Асимптоты гиперболы задаются уравнениями вида . Разделив обе части уравнения на 36, получим каноническое уравнение гиперболы: . То есть и . Тогда уравнения асимптот примут вид .
Тема:
Прямая линия в пространстве
Расстояние
между прямой ![]() и
плоскостью
и
плоскостью ![]() равно
…
равно
…
|
|
|
3 |
|
|
|
18 |
|
|
|
0 |
|
|
|
15 |
Решение:
Направляющий
вектор прямой имеет вид ![]() ,
а нормальный вектор плоскости:
,
а нормальный вектор плоскости: ![]() .
Скалярное произведение этих векторов
равно нулю:
.
Скалярное произведение этих векторов
равно нулю: ![]() .
Следовательно, прямая либо параллельна
плоскости, либо принадлежит ей. Тогда
расстояние между прямой и плоскостью
можно найти как расстояние между любой
точкой данной прямой и плоскостью. В
качестве такой точки возьмем, например,
.
Следовательно, прямая либо параллельна
плоскости, либо принадлежит ей. Тогда
расстояние между прямой и плоскостью
можно найти как расстояние между любой
точкой данной прямой и плоскостью. В
качестве такой точки возьмем, например, ![]() .
Расстояние от точки
до
плоскости
.
Расстояние от точки
до
плоскости ![]() найдем
по формуле
найдем
по формуле 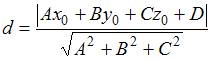 ,
то есть
,
то есть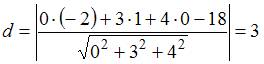
Тема: Плоскость в пространстве Уравнение плоскости, проходящей через точки , и , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Уравнение
плоскости, проходящей через точки ![]() ,
, ![]() и
и ![]() ,
не лежащие на одной прямой, имеет
вид
,
не лежащие на одной прямой, имеет
вид 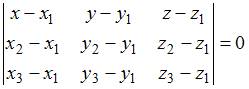 .
Подставим
числовые значения в полученное
уравнение:
.
Подставим
числовые значения в полученное
уравнение: 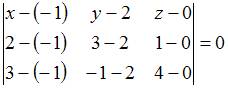 ,
или
,
или 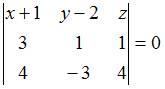 .
Раскрывая
определитель по первой строке,
получим
.
Раскрывая
определитель по первой строке,
получим ![]() ,
то
есть
,
то
есть
Тема: Прямоугольные координаты на плоскости Точки и лежат на одной прямой, параллельной оси ординат. Расстояние между точками и равно 6. Тогда положительные координаты точки равны …
|
|
|
, |
Тема:
Прямая линия в пространстве
Параметрические
уравнения прямой, параллельной оси ![]() и
проходящей через точку
имеют
вид …
и
проходящей через точку
имеют
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Параметрические уравнения прямой, проходящей через точку с направляющим вектором , имеют вид . За направляющий вектор прямой можно взять . Тогда или
Тема:
Прямоугольные координаты на
плоскости
Точки ![]() ,
, ![]() и
и ![]() лежат
на одной прямой. Тогда точка
делит
отрезок
лежат
на одной прямой. Тогда точка
делит
отрезок ![]() в
отношении …
в
отношении …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Делением
отрезка ![]() в
заданном отношении
в
заданном отношении ![]() называется
поиск такой точки
на
отрезке
,
которая удовлетворяет соотношению
называется
поиск такой точки
на
отрезке
,
которая удовлетворяет соотношению 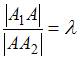 .
Тогда искомый параметр
будет
равен:
.
Тогда искомый параметр
будет
равен: 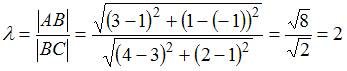
Тема:
Плоскость в пространстве
Общее
уравнение плоскости, проходящей через
точку ![]() параллельно
плоскости
параллельно
плоскости ![]() ,
имеет вид …
,
имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Уравнение
плоскости, параллельной плоскости
имеет
вид: ![]() .
Подставим координаты точки
в
это уравнение:
.
Подставим координаты точки
в
это уравнение: ![]() .
Тогда
.
Тогда ![]() .
.
Тема: Кривые второго порядка Мнимая полуось гиперболы равна … 3
Тема: Плоскость в пространстве Плоскости и перпендикулярны при значении , равном …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Прямая линия в пространстве Прямая параллельна плоскости , если параметр равен …
|
|
|
– 11 |
|
|
|
– 7 |
|
|
|
7 |
|
|
|
11 |
Решение:
Прямая
параллельна плоскости, если скалярное
произведение направляющего вектора
прямой ![]() и
нормального вектора плоскости
и
нормального вектора плоскости ![]() равно
нулю. То есть
равно
нулю. То есть ![]() ,
или
,
или ![]() .
.
Тема: Прямоугольные координаты на плоскости Даны три вершины параллелограмма: , , . Тогда четвертая вершина , противолежащая вершине , имеет координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема:
Кривые второго порядка
Соотношение  в
прямоугольной декартовой системе
координат задает …
в
прямоугольной декартовой системе
координат задает …
|
|
|
параболу |
|
|
|
гиперболу |
|
|
|
эллипс |
|
|
|
окружность |
Решение:
Вычислим 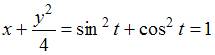 ,
то есть
,
то есть ![]() .
Тогда
в прямоугольной декартовой системе
координат данное уравнение задает
параболу с вершиной в точке
.
Тогда
в прямоугольной декартовой системе
координат данное уравнение задает
параболу с вершиной в точке ![]()
Тема: Прямоугольные координаты на плоскости В треугольнике с вершинами , и проведена медиана , длина которой равна …
|
|
|
4 |
|
|
|
|
|
|
|
16 |
|
|
|
|
Решение: Точка является серединой отрезка . Координаты середины отрезка определяются по формулам , . Подставляя в эти формулы координаты точек и , получим координаты точки : , . Расстояние между точками и можно найти по формуле . То есть
Тема: Плоскость в пространстве Общее уравнение плоскости, проходящей через точку параллельно плоскости , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Уравнение плоскости, параллельной плоскости имеет вид: . Подставим координаты точки в это уравнение: . Тогда .
Тема:
Кривые второго порядка
Фокусы
эллипса имеют координаты ![]() и
и ![]() ,
а его эксцентриситет равен 0,6. Тогда
каноническое уравнение эллипса имеет
вид …
,
а его эксцентриситет равен 0,6. Тогда
каноническое уравнение эллипса имеет
вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Каноническое
уравнение эллипса имеет вид 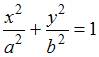 ;
фокусы эллипса имеют координаты
;
фокусы эллипса имеют координаты ![]() и
и ![]() ,
где
,
где ![]() ,
а эксцентриситет
,
а эксцентриситет ![]() .
Тогда
.
Тогда ![]() ,
, ![]() ,
, ![]() .
Следовательно,
получаем уравнение
.
Следовательно,
получаем уравнение
Тема: Плоскость в пространстве Общее уравнение плоскости, проходящей через точку перпендикулярно прямой , имеет вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Уравнение плоскости, проходящей через точку с нормальным вектором , имеет вид: . Так как эта плоскость перпендикулярна прямой , то в качестве нормального вектора плоскости можно использовать направляющий вектор этой прямой, то есть . Тогда или .
Тема: Прямоугольные координаты на плоскости Даны точки и . Тогда координаты точки , симметричной точке относительно точки , равны …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тема: Прямая линия в пространстве Параметрические уравнения прямой, параллельной оси и проходящей через точку имеют вид …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение: Параметрические уравнения прямой, проходящей через точку с направляющим вектором , имеют вид . За направляющий вектор прямой можно взять . Тогда или .
Тема:
Кривые второго порядка
Центр
окружности ![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Окружность
радиуса
с
центром в точке ![]() задается
на плоскости уравнением
.
Выделим в уравнении
полные
квадраты:
задается
на плоскости уравнением
.
Выделим в уравнении
полные
квадраты: ![]() ,
или
,
или ![]() .
Тогда
центр окружности имеет координаты
.
Тогда
центр окружности имеет координаты
Тема:
Кривые второго порядка
Вершина
параболы ![]() имеет
координаты …
имеет
координаты …
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
Выделим
в уравнении
полный
квадрат: ![]() или
или ![]() .
Тогда вершина параболы имеет координаты
.
Тогда вершина параболы имеет координаты
Видеоуроки ЕГЭ
Математика (1)
Информатика (2)
Физика (2)
Русский язык (0)
Обществознание (0)
История (0)
Английский язык (2)
Биология (0)
География (0)
Химия (0)
Экономика (1)
Разделы
Решебники
Презентации PowerPoint
Расчетки
Материалы
Шпаргалки
Лабораторные работы
Разное
Курсовые
Дипломы
Решение задач
Видеоуроки
СтудентLife
Новости
Юмор
Это интересно
ответы i-exam
Теория государства и права
Культурология
Метрология
Безопасность жизнедеятельности
Философия
Информатика
КП РФ
Политология
История
Материаловедение i-exam
Психология и педагогика
Математика
Отправка материалов!
Физика
|
ДЕ3.Дифференциальная геометрия