10. Лоду n-го порядка. Общая теория

(1)

f(x)0, то уравнение (1) называется линейным неоднородным ДУn-го порядка.

f(x)=0, то уравнение (1) называется линейным однородным ДУ n-го порядка.

Если P₁(x),P₂(x),..,P_n(x) (коэффициенты) и правая часть f(x) непрерывны на [a,b] => по теореме существования и единственности существует единственное решение задачи Коши, т.е. уравнение (1) удовлетворяет начальным условиям: y(x₀)=x₀, y¹(x₀)=y₀¹,…,y^n-1(x₀)=y₀^n-1, где x₀ [a,b]

Линейный дифференциальный оператор:

L[y]= yⁿ+P₁(x)y^n-1+…+P_n(x)y (2)

1. L(C_y)=CL(y)

2. L(y₁+y₂)=L(y₁)+L(y₂)

L(y) = f(x) (1) ЛНОДУ

L(y) = 0 (3) ЛОДУ

Свойства решений:

(1)

Более короткая запись: L(y) = 0 (1’)

L[y]= yⁿ+P₁(x)y^n-1+…+P_n(x)y (2) – минимальный дифференциальный оператор

Свойства:

1) Линейное

Пусть y₁(x),y₂(x) – решения ДУ (1) или (1’) => C₁y₁(x)+C₂y₂(x) – решение (1) или (1’)

C₁ и C₂ – произвольные константы

Доказательство вытекает из свойств линейного оператора:

L(C₁y₁+C₂y₂) = C₁L[y₁] + C₂L[y₂]=0

2) Пусть U(x) + iV(x) – решение ДУ (1) => U(x) и V(x) - решение (1)

Док-во:

L(U+iV) = 0

L[U]+iL[V] => L[U] = 0 и L[V] = 0

О₁: y₁(x),y₂(x),…,y_n(x) называется линейно-зависимым на отрезке [a,b], если существует , из которых хотя бы одно отлично от нуля, что выполняется равенствоy₁(x)+y₂(x)+…+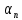y_n(x)=0 (3) при x[a,b].

О₂: если тождество (3) выполняется только при нулевых коэффициентах, тогда эта система функций называется линейно-независимой

Пример линейно-независимой системы:

1,x,x²,…,xⁿ – линейно-независима на отрезке [a,b]

3) Пусть y₁(x),y₂(x),…,y_n(x) линейно-независима на [a,b] => на этом же отрезке определитель W(x)(дубль v)

(4)

(4) – определитель Вронского тождественно равен 0, т.е. W(x), при.

4) Линейно-независимые на отрезке [a,b] функции y₁(x),y₂(x),…,y_n(x) являются ЛОДУ n-го порядка (1) с непрерывными на [a,b] коэффициентами P₁(x),P₂(x),…,P_n(x) => определитель Вронского не обращается в ноль ни в одной точке .

5) Теорема о структуре общего решения ЛОДУ n-го порядка

Пусть y₁(x) y₂(x), .... y_n(x) является n линейно независимых на отрезке [a, b] решений ЛОДУ n - го порядка с некоторыми коэффициентами на [a, b], следовательно их линейная комбинация с произвольными константами

y(x) = C_iy_i(x) (5)

являются общими решениями ЛОДУ n-Го порядка (1)

Доказательство:

y(x) = C_iy_i(x) - решение, это ясно из свойства один

Начальное условие:

y(x₀) = y₀, y'(x₀) = y'₀, ... y^(n-1)(x₀) = y₀^(n-1) (6)

x ϵ [a, b]

y(x) = C_iy_i(x₀) = y₀

y(x) = C_iy'_i(x₀) = y'₀

y(x) = C_iy_i^(n-1) = y₀^(n-1)

Это получилось СЛАУ относительно С

W(x)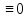

11. Теорема о структуре общего решения лоду n-го порядка (Если надо будет, то это свойство 5)

Пусть y₁(x) y₂(x), .... y_n(x) является n линейно независимых на отрезке [a, b] решений ЛОДУ n - го порядка с некоторыми коэффициентами на [a, b], следовательно их линейная комбинация с произвольными константами

y(x) = C_iy_i(x) (5)

являются общими решениями ЛОДУ n-Го порядка (1)

Доказательство

y(x) = C_iy_i(x) - решение, это ясно из свойства один

Начальное условие:

y(x₀) = y₀, y'(x₀) = y'₀, ... y^(n-1)(x₀) = y₀^(n-1) (6)

x ϵ [a, b]

y(x) = C_iy_i(x₀) = y₀

y(x) = C_iy'_i(x₀) = y'₀

y(x) = C_iy_i^(n-1) = y₀^(n-1)

Это получилось СЛАУ относительно С

определитель(треугольник) = ᴡ(якобиан)(x₀) = 0