1. Задачи, приводящие к оду
Задача 1 (Задача о радиоактивном распаде)
Составить уравнение радиоактивного распада вещества при условии, что скорость распада пропорциональна количеству вещества в любой момент времени t.
Решение
m(t) - количество вещества
-
скорость распада
=
- mk (1)
m' + mk = 0
Задача 2 (Задача о свободном падении тела в среде с сопротивлением)
Произвольное тело массой m свободно падает в воздушной среде. составить дифференциальное уравнение относительно скорости паления при условии того, что скорость пропорциональна силе сопротивления.
Решение
ma = mg - kv (2)
=
ma
mv' + kv = mg (2')
Задача 3 (Задача об охлаждении нагретого тела)
В среде с температурой среды Tc находится нагретое тело. Составить дифференциальное, описывающие процесс охлаждения тела в этой среде при условии, что v охлаждения пропорциональна разности TЛ - Tс
Решение
T(t)
=
- (Tл
- Tc)
(3)
T' + k(Tл - Tc) = 0 (3')
2.Оду 1-го порядка. Общие понятия
F(x, y, y') = 0 (1)
y' = f(x, y) (1')
Начальное условие одно, так как порядок 1
НУ : y(x0) = y0 (2)
(1) - (2) - называется задача Коши для дифференциального уравнения (1)
y
=
(x)
- решение, график его решения называется
интегральная кривая.
О1
Общим решением (ОР) дифференциального
уравнения называется однопараметрическое
семейство функций y=
(x,
С), которое удовлетворяет 2 условиям
1)
y
=
(x,
С) - является решением при любом С.
2)
при любом НУ вида (2) существует такое C
= C0,
что y
=
(x,
С0)
- решение удовлетворяет этому НУ
y=
(x,
С) - ОР
О2
Частным решением (ЧР) ОДУ называется
решение, полученное из общего решения
при фиксированном C
= C0,
то есть y
=
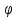(x,
С0)
- ЧР
Иногда
общее решение получается не в виде y
=
(x,
С), а в виде ϕ (x,
y,
C)
= 0 - интеграл.
Частный интеграл - решение, полученное из общего интеграла при фиксированном значении C, то есть
C = C0
ϕ (x, y, C0) - частный интеграл
Теорема (О существовании единственности решения задачи Коши для ОДУ 1-го порядка)
Пусть имеем задачу Коши для ОДУ 1-го порядка
y' = f(x,y), y(x0) = y0
Пусть
f
непрерывна в некоторой области D
⊂
R2
и M0(x0,
y0)
∈
D,
тогда
в некоторой окрестности точки x0:(x0-
δ, x0+δ),
тогда существует по меньшей мере одно
решение y
= 𝜑(x)
этого дифференциального уравнения. При
дополнительном условии ограниченности
вот такой частной производной
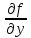в
некоторой окрестности точки M0,
это решение единственно и удовлетворяет
НУ (без доказательства)
3. ОДУ 1-го порядка с разделяющимися переменными.
y' = f1(x)*f2(y) (1)
M1(x)*M2(y)dx + N1(x)*N2(y)dy = 0 (2)
N1(x)*N2(y)dy = - M1(x)*M2(y)dx
dy
= -
dx
=
-
4. Однородное (относительно переменных) оду 1-го порядка
О1 Называется однородным к-го порядка если выполняется следующее равенство
f(λx, λy) =λk f(x, y)
Если к = 0, то это однородное уравнение нулевого порядка.
О2 ОДУ y'= f(x, y) Называется однородное(относительно переменных), если f(x, y) - однородное нулевого порядка
y'=
(
)
(1)
=
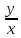t
y=tx
y' = t'x + t
t'x
+ t=
x=
- t
=
=
