1. Постановка задачи

В курсовой работе необходимо:

• разработать модель многоопорной колебательной системы (транспортного механизма);

• на основе полученной модели произвести тестирование данного транспортного средства в зависимости от различных внутренних и внешних параметров, действующих на систему;

• эргономически обоснованно реализовать выбор определенных параметров, влияющих на комфортабельность места водителя;

В качестве инструментариев к реализации поставленной задачи необходимо использовать следующие пакеты:

• MathCAD;

• MATLAB.

2. Вывод системы формул для расчёта оптимизационной модели автомобиля

2.1. Расчётная схема многоопорной машины с указанием варьируемых параметров

Кратко охарактеризуем её. Машина представляет собой корпус М₁, который получает кинематическое воздействие от дороги ,,посредством трёх опор. Эти опоры состоят из параллельно соединённой пружины и демпфера () и двух пружинk₂, k₃ . Сверху на корпусе М₁ расположена массы М_2, М₃ . Эти массы соединяется с корпусом М₁ при помощи двух опор: соединённых параллельно пружины и демпфера (k₆ - с₃), пружины , пружиныk₄ и демпфера с₂. На массе М₃ в свою очередь расположена масса М₄, соединенная с М₃ при помощи пружины k₆. Расстояние между опорами k₂ и k₃ равно l₃, oт центра корпуса до опор k₂ и k₁ - c₁ равны l₂ и l₁ соответственно. Расстояние от центра корпуса до опор k₅ и k₆ – c₃ и равно соответственно l₅ и l₅+l₆. Расстояние от центра корпуса до центра корпуса М₂ до равно l₅+l₆+l₇. Расстояние от центра корпуса до центра массы М₃ (М₄) равно l₄ . Запишем исходные данные модели.

Параметры пружин:

Параметры демпферов:

Длины:

Моменты инерции:

Функции дороги:

Для оптимизации было выбрано линейное ускорение массы М₂ при варьировании параметров ,.

2.2. Выбор обобщенных перемещений.

Целесообразно рассматривать относительные перемещения ,,,,,, 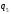которые отсчитываются относительно земли:

q₁ — угол поворота корпуса относительно горизонта;

q₂ — вертикальное перемещение массы корпуса относительно грунта;

q₃ — угол поворота массы М2 относительно горизонта;

q₄ — вертикальное перемещение массы М2 относительно грунта;

q₅ — вертикальное перемещение массы М3 относительно грунта;

q₆ — вертикальное перемещение массы М4 относительно грунта;

В дальнейшем будем использовать в формулах для кинетической энергии относительные перемещение, а в формулах для удлинения пружин – обобщённые. Этот подход усложнит формулу кинетической энергии, однако упростит формулы для потенциальной энергии и диссипативной функции.

2.3. Составление выражений для удлинения и скорости удлинения упругих элементов

Перед началом записи выражений удлинения упругих элементов, определим следующие правило знаков: знак “-” будет браться, если упругий элемент сжимается, знак “+“ будет браться, если упругий элемент растягивается.

Запишем значение удлинения для каждой из присутствующих в многоопорном механизме пружин: , гдеi соответветствует номеру пружины:

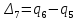
Таким образом, выражения для скоростей удлинения примут вид:

Записав абсолютные перемещения и выражения для удлинения упругих элементов, а также выражения для скоростей, имеем все данные для составления выражений кинетической, потенциальной энергий и диссипативной функции.

2.4. Полная кинетическая энергия системы.

Ее выражение и частные производные

Полная кинетическая энергия системы:

Вычислим частные производные вида:

Они понадобятся нам для составления уравнения Лагранжа 2-го рода.

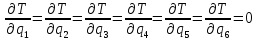
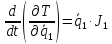
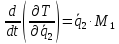
2.5. Полная потенциальная энергия системы.

Ее выражение и частные производные

Выражение для потенциальной энергии системы:

Определим частные производные вида:

которые понадобятся при составлении уравнений Лагранжа 2-го рода.

2.6. Диссипативная функция. Ее выражение и частные производные

Выражение для диссипативной функции:

Найдем частные производные вида:

2.7. Составление системы уравнений Лагранжа 2-го рода

В систему уравнений Лагранжа второго рода (количество уравнений равно количеству неизвестных, т.е. количество уравнений равно шести) будут входить уравнения типа:

где - вектор обобщённых внешних воздействий (на модель оказывают воздействие только функции дороги, поэтому этот вектор равен нулю),- найденные ранее частные производные от потенциальной энергии и диссипативной функции.

Система Лагранжа 2-го рода: