56Законы сохранения и свойства симметрии пространства-времени

Законы сохранения - фундаментальные физические законы, согласно которым при определенных условиях некоторые физические величины не изменяются с течением времени. Законы сохранения связаны с симметриями физических систем (теорема Нётер). Так, законы сохранения энергии, импульса и момента импульса являются следствиями пространственно-временных симметрий (соответственно: однородности времени, однородности и изотропности пространства). При этом перечисленные свойства пространства и времени в аналитической механике принято понимать как инвариантность лагранжиана относительно изменения начала отсчета времени, переноса начала координат системы и вращения ее координатных осей.

57Удар абсолютно упругих и неупругих твердых тел

Удар – кратковременное взаимодействие соприкасающихся тел, приводящее к значительному изменению их движения.

Абсолютно упругий –удар, при кот. полная мех. энергия системы тел сохраняется.

Абсолютно неупругий –удар, при кот. тела, после соударения либо двигаются с одинаковой скоростью, находясь в соприкосновении друг с другом и сохр. деформации, либо покоятся.

Динамика ТТ

58Момент инерции м.точки и т.т. относительно неподвижной оси

По определению момент инерции твёрдого тела равен I==

где символом m_i обозначена элементарная масса , r_i – ее расстояние

от оси вращения.

Элементарная масса ∆ m_iравна произведению плотности тела ρ_i в дан-ной точке на соответствующий элементарный объём ∆V_i:

m_i =∆V_iρ_i

Следовательно, момент инерции тела можно представить в виде

59Главные оси и главн моменты инерц т.т.

Момент инерции тела относительно осей – наз. главным моментом.

Главными осями инерции твердого тела называются такие три взаим-но перпендикулярных оси, проходящих через центр масс, относительно ко-торых один из главных моментов инерции тела является максимальным,

второй– минимальным, а третий имеет промежуточную величину.

60Моменты инерции некотор тел регулярной формы -

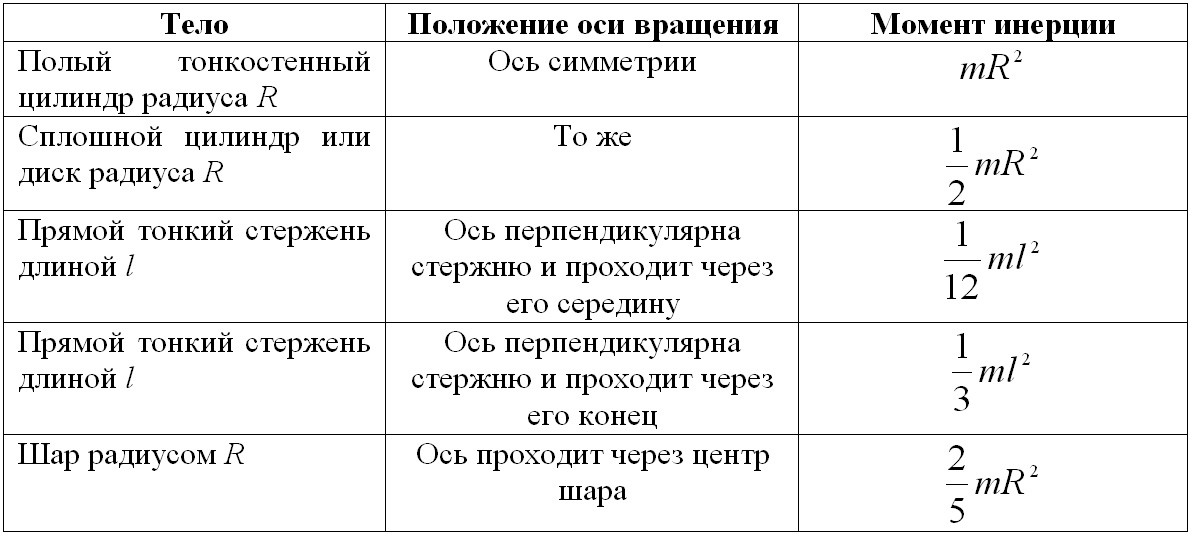
Шар I=2/5mR² диск I=1/2mR² Сфера I=2/3mR² обруч I=mR² стержень I=1/12ml²

61Теорема Штейнера – момент инерции тела относительно произвольной оси равен сумме моментов инерции этого тела относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы этого тела на квадрат расстояния между ними. I= I₀+mR²

62Момент силы относительно точки и оси – Связь момента силы относительно оси с векторным моментом силы относительно точки

Проведем через точку O, где задан момент силы относительно точки Mo(F) декартовы оси координат x, y, z (рисунок 1.4).

Момент силы относительно точки можно представить в виде суммы трех векторов

Mo(F) = Mx(F)i + My(F)j + Mz(F)k.

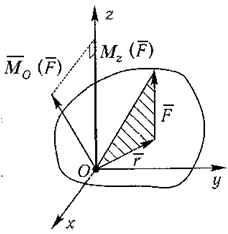
Эти вектора являются моментами силы относительно осей x, y, z:

Mx(F) = |Mo(F)|cos(i, Mo(F)),

My(F) = |Mo(F)|cos(j, Mo(F)),

Mz(F) = |Mo(F)|cos(k, Mo(F)),

Момент силы относительно оси равен проекции на эту ось момента силы относительно любой точки на оси.

63Ур-ние движения ТТ, вращающегося относительно неподвижной оси –

Произведение момента инерции твердого тела относительно непод-вижной оси вращения на угловое ускорение равно моменту внешних сил от-носительно этой оси

I=εM

64Момент импульса относительно точки и оси –Момент силы относительно точки О - это вектор, модуль которого равен произведению модуля силы на плечо - кратчайшее расстояние от точки О до линии действия силы. Направление вектора момента силы перпендикулярно плоскости, проходящей через точку и линию действия силы, так, что глядя по направлению вектора момента, вращение, совершаемое силой вокруг точки О, происходит по часовой стрелке.Если известен радиус-вектор r⃗точки приложения силы F⃗относительно точки О, то момент этой силы относительно О выражается следующим образом:M⃗O(F⃗)=r⃗×F⃗.Момент силы относительно оси Проекция момента силы относительно точки на некоторую ось, проходящую через эту точку называется моментов силы относительно оси. Момент силы относительно оси вычисляется как момент проекции силы F⃗на плоскость Π,перпендикулярную оси, относительно точки пересечения оси с плоскостью Π:Mz(F⃗)=Mz(F⃗Π)=±FΠh. Знак момента определяется направлением вращения, которое стремится придать телу сила F⃗Π. Если, глядя по направлению оси Oz сила вращает тело по часовой стрелке, то момент берется со знаком ``плюс'', иначе - ``минус''.