3.3 Проектирование закругления малого радиуса

На закруглении с радиусами менее рекомендуемых предусматривают переходные кривые и виражи, а также уширение проезжей части. Схема закругления малого радиуса представлена на рис.3.2.







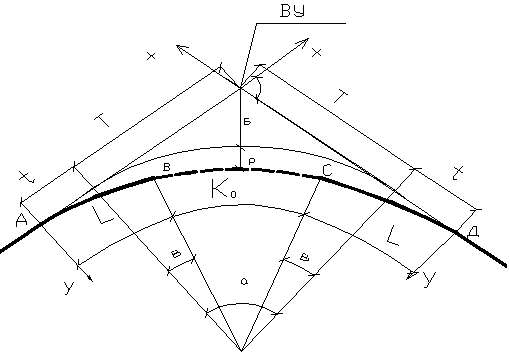
Рисунок 3.2 - Элементы закругления с симметричными переходными кривыми

Проектирование плана закругления малого радиуса ведут в следующей последовательности.

Вычисляют длину переходной кривой L:

, м, (3.5)

где V – расчетная скорость для дороги принятой категории, км/ч;

J – допускаемая скорость нарастания бокового ускорения, м/с³, принимают равной 0,3 для радиусов закруглений 300 м и более и 0,4 для радиусов менее 300 м, в обычных условиях и соответственно 0,5; 0,7 в стесненных условиях;

R – радиус круговой кривой, м.

Полученные по формуле (3.5) значения L сопоставляют с минимальными по нормам проектирования (табл. 3.1). Для дальнейшего расчета принимают большее значение длины переходной кривой.

Далее находят угол β, на который уменьшается круговая кривая при вписывании одной переходной кривой:

, градусы. (3.6)

Проверяют условие возможности разбивки закругления с переходной кривой:

, (3.7)

где α – угол поворота трассы (по заданию).

Если условие не выполнено, то следует изменить длину переходной кривой или угол поворота трассы.

Вычисляют длину круговой кривой К₀:

, м, (3.8)

где – угол поворота трассы в градусах.

Закругления с переходными кривыми обычно выносят на местность методом прямоугольных координат X и Y, помещая начало координат в начало первой переходной кривой (т. А на рис. 3.2) и в конец второй (т. Д).

Координаты конца переходной кривой определяют по формуле:

Х_в (3.9)

Y_в ,(3.10)

где Х_в и Y_в – координаты конца переходной кривой.

Далее определяют смещение t и сдвижку р переходной кривой:

t = X_в – R sin β; p = Y_в – R (1 – cos β), (3.11)

Затем вычисляют тангенс Т и домер D закругления малого радиуса:

Т = (R + р) tg (α/2), (3.11)

D = 2 (T + t) – (2L + К₀). (3.12)

Пикетное положение основных точек закругления малого радиуса с переходной кривой определяют по формулам:

т. А (начало закругления) НЗ = ВУ – (Т + t);

т. В (начало круговой кривой) НКК = НЗ + L;

т. С (конец круговой кривой) ККК = НЗ + L + К₀;

т. Д (конец закругления) КЗ = НЗ + 2L + К₀.

Проверка расчета КЗ = ВУ + (Т + t) – Д.

Пикетное положение основных точек закругления с радиусами более рекомендуемых без переходной кривой определяют по формулам:

НЗ = ВУ – Т ; КЗ = НЗ + К; КЗ = ВУ + Т – Д.

На каждом закруглении при известных значениях a, R, L вычисляют элементы закругления, и пикетные положения основных точек закругления с точностью до 0,01м.

3.4 Разбивка пикетажа и составление ведомости прямых и кривых

Разбивка пикетажа включает нанесение пикетов и плюсовых точек на трассе с помощью измерителя и установление пикетного положения вершин углов поворота. Обычно начало хода (НХ) принимают равным нулю (ПК0).

Протяженность участков ломаной трассы измеряют по топографической карте и с учетом масштаба определяют их длину.

Пикетное положение первой вершины (ВУ1) определяют по формуле

ВУ1 = НХ + П₁ (3.12)

Пикетное положение второй вершины (ВУ2) определяют по формуле

ВУ2 = ВУ1 + П₂ – Д₁ ; (3.13)

Пикетное положение конца хода (КХ) определяют по формуле

КХ = ∑Пi - ∑Дi _. (3.14)

На каждом закруглении при известных значениях a, R, L вычисляют остальные элементы закругления с точностью до 0,01м, пикетные положения основных точек закругления.

Затем определяют длины оставшихся прямолинейных участков трассы, оставшихся после вписывания закруглений.

П₁ = НЗ₁ – НХ; П₂ = НЗ₂ – КЗ₁; П₃ = КХ – КЗ₂;

По топографической карте местности определяют дирекционный угол (ДУ) – угол, измеренный по часовой стрелке, между северным направлением вертикальной линией километровой сетки карты и направлением прямой (рис. 3.2).

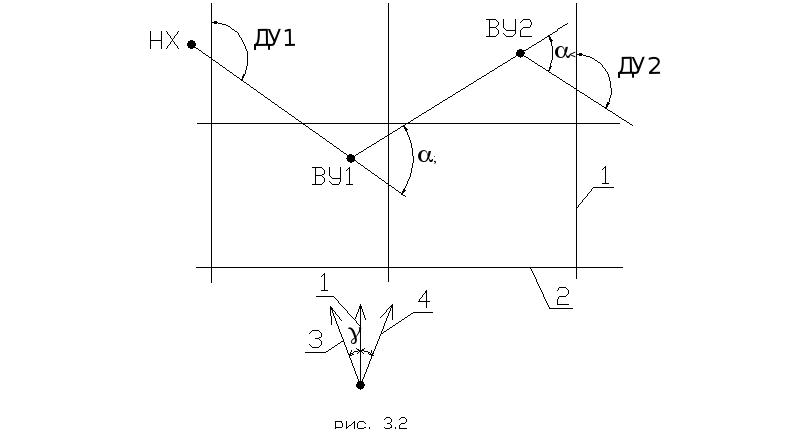
Рисунок 3.3 - Схема к вычислению дирекционного угла:

1 – вертикальная линия километровой сетки на карте; 2 - нижний край карты; 3 – направление магнитного меридиана; 4 – направление истинного меридиана.

Для выноски трассы на местность вычисляют магнитный азимут. Магнитный азимут (А) - угол, измеренный по часовой стрелке, между северным направлением магнитного меридиана и направлением прямой.

(3.6)

где - угол между вертикальной линией сетки карты и магнитным меридианом, указан внизу карты местности.

По полученной величине азимута А₁ , вычисляют значение магнитных азимутов остальных линий.

Азимут линии определяют по формуле

(3.7)

В формуле (3.7) знак «+» принимают, если трасса поворачивает вправо на угол , и знак «-», если она поворачивает влево на угол.

Румб (магнитный) – острый угол между ближайшим концом меридиана (северного или южного) и направлением прямой. По величине азимутов вычисляют румбы линии.

Если азимут находится в пределах:

- от 0 до 90 градусов, то румб линии по направлению будет - северо-восток (СВ), а величина угла равна азимуту (А);

- от 90 до 180 градусов, то румб линии по направлению будет - юго-восток (ЮВ), а величина угла равна (180 - А );

- от 180 до 270 градусов, то румб линии по направлению будет - юго-запад (ЮЗ), а величина угла равна (А - 180);

- от 270 до 360 градусов, то румб линии по направлению будет - северо-запад (СЗ), а величина угла равна (360 - А).

Далее составляется ведомость углов поворота, прямых и кривых. Форма такой ведомости приведена в табл. 3.1.

Т а б л и ц а 3.1

Me пп	а		ВУ		R	Т	К	Б	Д	L	t		Р	Ко
	лево	право	ПК	+
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

НЗ		НКК (НПК)		ККК (НПК)		КЗ		Длина прямой	Румб
ПК	+	ПК	+	ПК	+	ПК	+
16	17	18	19	20	21	22	23	24	25

В первой строке в графе 1 ставят НХ (начало хода) и его пикетное положение (гр. 4, 5), в последней строке - аналогично КХ (конец хода). В промежуточных строках приводят данные по каждому закруглению. Если есть переходная кривая, то графа 8 не заполняется. При отсутст­вии переходной кривой не заполняются графы 11-15 и 18-21. Суммируют столбцы 7, 10, 11, 12, и 15, получают .

Правильность составления ведомости прямых и кривых проверяют:

по длине трассы

(3.8)

по домерам

(3.9)