1.7. Трение Трение скольжения

При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхностей соприкосновения возникает сила трения скольжения (трение первого рода).

Пусть на тело действует плоская система активных сил и тело находится в равновесии, соприкасаясь с шероховатой поверхностью другого тела (рис. 16).

Сила реакциишероховатой поверхности будет складываться из нормального давления, направленного по общей нормали к поверхности соприкосновения, и силы трения скольженияпри покое.

Для силы трения скольжения справедливы законы Кулона:

1. С

   Рис. 16

   ила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного или реального скольжения тела под действием приложенных сил. Сила трения при покое зависит от активных сил и ее модуль заключен между нулем и максимальным значением, которое достигается в момент выхода тела из положения равновесия, т.е.

.

2. Максимальная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей. Из этого закона следует, что для того, чтобы сдвинуть, например, кирпич, надо приложить одну и ту же силу независимо от того, какой гранью он положен на поверхность, широкой или узкой.

3. Максимальная сила трения скольжения пропорциональна нормальному давлению (нормальной реакции), т. е.

, (30)

где безразмерный коэффициент называют коэффициентом трения скольжения; он не зависит от нормального давления.

Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей, т.е. от величины и характера шероховатости, влажности, температуры и других условий. Коэффициент трения скольжения в зависимости от различных условий устанавливается экспериментально.

Трение качения

Если одно тело, например цилиндрический каток, катить или стремиться катить по поверхности другого тела, то кроме силы трения скольжения из-за деформации поверхностей тел дополнительно возникает пара сил, препятствующая качению катка. Явление возникновения пары сил, препятствующей качению, называют трением качения или трением второго рода.

А

Рис. 17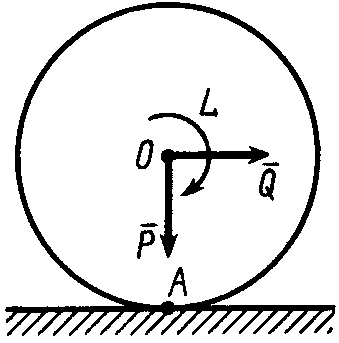

ктивные силы, действующие на катки в виде колес (рис. 17), кроме силы тяжестиобычно состоят из силы, приложенной к центру колеса параллельно общей касательной в точке, и пары сил с моментом, стремящейся катить колесо, называемое в этом случаеведомо-ведущим. Если , а, то колесо называютведомым; если , а, товедущим. Ведомо-ведущими являются колеса локомотива, идущего вторым в составе поезда.

Приведем активные силы в общем случае к точке . В этой точке получим главный вектор этих сили пару сил, момент которой равен главному моменту(рис. 18).

П

Рис. 18

ри равновесии катка, т.е. когда каток не катится и не скользит по плоскости, активные силы уравновешиваются силами реакций связи и, следовательно,

; .

Изменив активные силы, приложенные к катку так, чтобы увеличивался момент пары активных сил, стремящейся катить каток. Пока каток находится в равновесии, увеличивается и равный ему по числовой величине, но противоположный по направлению моментпары сил, препятствующий качению катка и возникающий от действия на каток неподвижной плоскости. Наибольшее значениедостигается в момент начала качения катка по плоскости.

Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующей качению:

1. Наибольший момент пары сил, препятствующей качению, в довольно широких пределах не зависит от радиуса катка.

2. Предельное значение момента пропорционально нормальному давлению, а следовательно, и равной ему нормальной реакции:

. (31)

Коэффициент пропорциональности называют,коэффициентом трения качения при покое или коэффициентом трения второго рода. Из формулы (31) следует, что имеет размерность длины.

3. Коэффициент трения качения зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости.