Лекция № 10

3.6.8. Уравнения Лагранжа второго рода

Уравнения Лагранжа можно рассматривать как алгоритм получения дифференциальных уравнений движения системы, т.е. дифференциальных уравнений относительно обобщенных координат.

Уравнения Лагранжа первого рода для голономной механической системы с степенями свободы, на которую наложены идеальные связи имеют вид:

, , (231)

где – обобщенные координаты; величина– обобщенная скорость;–обобщенная сила, отнесенная к обобщенной координате;– кинетическая энергия системы.

Число уравнений Лагранжа равно числу степеней свободы системы.

При составлении уравнений Лагранжа можно рекомендовать следующий порядок операций.

1. Вычислить кинетическую энергию системы в ее движении относительно инерциальной системы отсчета.

2. Выбрав обобщенные координаты, число которых равно числу степеней свободы системы, преобразовать кинетическую энергию к обобщенным координатам.

3. Выполнить операции дифференцирования кинетической энергии, предусмотренные уравнениями Лагранжа.

4. Вычислить одним из способов, указанных в пункте 3.5.6. обобщенные силы системы.

5. Приравнять величины левой и правой частей, входящих в уравнения Лагранжа.

3.7. Решение задач динамики

Пример 7. На вертикальном участкетрубы (рис. 55) на грузмассойдействуют сила тяжести и сила сопротивления; расстояние от точки, где, до точкиравно. На наклонном участкена груз действуют сила тяжести, сила трения скольженияс коэффициентом тренияпеременная сила, заданная в ньютонах.

Д

Рис. 55

ано: кг,, гдекг/м,м/с,м,,.

Определить: на участке.

Решение:

1. Рассмотрим движение груза на участке , считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силыи. Проводим осьи составляем дифференциальное уравнение движения груза в проекции на эту ось:

, или, . (232)

Далее находим ,. Подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что, получим

, или . (233)

Введем для сокращения записей обозначения:

м^–1, м²/с², (234)

где при подсчете принято м²/с². Тогда уравнение (233) можно представить в виде:

. (235)

Разделяя в уравнении (235) переменные, а затем беря от обеих частей интегралы, получим

и . (236)

По начальным условиям при , что даети из равенства (236) находимили. Отсюда

и .

В результате находим:

. (237)

Полагая в равенстве (237) м, и заменяяиих значениями (234), определим скорость ив груза в точке(м/с, число):

и м/с. (238)

2. Рассмотрим теперь движение груза на участке . Найденная скоростьбудет для движения на этом участке начальной скоростью (). Изображаем груз (в произвольном положении) и действующие на него силы,,и. Проведем из точкиосиии составим дифференциальное уравнение движения груза в проекции на ось:

,

или

, (239)

где . Для определениясоставим уравнение в проекции на ось. Так как, получим, откуда. Следовательно,. Кроме того,и уравнение (239) примет вид:

. (240)

Разделив обе части равенства на , вычисливи, подставим эти значения в (9). Тогда получим:

. (241)

Умножая обе части уравнения (241) на и интегрируя, найдем:

. (242)

Будем теперь отсчитывать время от момента, когда груз находится в точке , считая в этот момент . Тогда при , где дается равенством (238). Подставляя эти величины в (242), получим

.

При найденном значении уравнение (242) дает:

. (243)

Умножая здесь обе части на и снова интегрируя, найдем

. (244)

Так как при , тои окончательно искомый закон движения груза будет

. (245)

где – в метрах,– в секундах.

Ответ: , – в метрах,– в секундах.

П

Рис. 56

ример 8.В центре тяжести тележки массой, движущейся по гладкой горизонтальной плоскости, укреплен невесомый стерженьдлинойс грузоммассойна конце (рис. 56). В момент времени, когда скорость тележки, стерженьначинает вращаться вокруг осипо закону.

Дано: кг,кг,м/с,м,рад, где– в секундах.

Определить: закон изменения скорости тележки .

Решение:

1. Рассмотрим механическую систему, состоящую из тележки и груза , в произвольном положении (рис. 56). Изобразим действующие на систему внешние силы: силы тяжести , и реакции плоскости , . Проведем координатные оси так, чтобы ось была горизонтальна.

Чтобы определить , воспользуемся теоремой об изменении количества движения системы в проекции на ось . Так как все действующие на систему внешние силы вертикальны (рис. 56), то и теорема дает

, откуда . (246)

Для рассматриваемой механической системы , где и – количества движения тележки и груза соответственно ( – скорость тележки, – скорость груза по отношению к осям ). Тогда из равенства (246) следует, что

или . (247)

2. Определение . Рассмотрим движение груза как сложное, считая его движение по отношению к тележке относительным (это движение, совершаемое при вращении стержня вокруг оси), а движение самой тележки – переносным. Тогда и

. (248)

Но и, следовательно, . Вектор направлен перпендикулярно стержню и численно .

Изобразив этот вектор на рис. 56 с учетом знака , найдем, что . Окончательно из равенства (248) получим

. (249)

(В данной задаче величину можно еще найти другим путем, определив абсциссу груза , для которой, как видно из рис. 56, получим , тогда , где , .)

3. При найденном значении равенство (247), если учесть, что , примет вид

. (250)

Постоянную интегрирования определим по начальным условиям: при,. Подстановка этих величин в уравнение (250) даети тогда из (250) получим:

.

Отсюда находим следующую зависимость скорости и тележки от времени

. (251)

Подставив сюда значения соответствующих величин, находим искомую зависимость и от от:

. (252)

Ответ:

Пример 9. Однородная горизонтальная платформа (прямоугольная со сторонами и), имеющая массу, жестко скреплена с вертикальным валом и вращается вместе с ним вокруг осис угловой скоростью(рис. 57,а). В момент временина вал начинает действовать вращающий момент, направленный противоположно; одновременно грузмассой, находящийся в желобев точке, начинает двигаться по желобу (под действием внутренних сил) по закону.

Дано: кг,кг,с^–1, м,(гдев метрах,– в секундах),, где.

Определить: закон изменения угловой скорости платформы .

а) б)

Рис. 57

Решение:

1. Рассмотрим механическую систему, состоящую из платформы и груза . Для определенияприменим теорему об изменении кинетического момента системы относительно оси:

. (253)

Изобразим действующие на систему внешние силы: силы тяжести , и реакции ,и вращающий момент. Так как силы и параллельны оси , а реакциииэту ось пересекают, то их моменты относительно осиравны нулю. Тогда, считая для момента положительным направление против хода часовой стрелки, получими уравнение (253) примет такой вид:

. (254)

Умножая обе части этого уравнения на и интегрируя, получим

. (255)

Для рассматриваемой механической системы

, (256)

где и– кинетические моменты платформы и грузасоответственно.

2. Определение . Так как платформа вращается вокруг оси, то. Значениенайдем по теореме Гюйгенса:(– момент инерции относительно оси, параллельной осии проходящей через центрплатформы).

Но, как известно,

.

Тогда

.

Следовательно,

. (257)

3. Для определения обратимся к рис. 57,б и рассмотрим движение грузакак сложное, считая его движение по платформе относительным, а вращение самой платформы вокруг осипереносным движением. Тогда абсолютная скорость груза . Так как груз движется по закону, то ; изображаем вектор на рис. 57,б с учетом знака (принаправление было бы противоположным). Затем, учитывая направление , изображаем вектор (); численно . Тогда, по теореме Вариньона,

. (258)

Из рис. 57,б видно, что . Подставляя эту величину в равенство (6), находим.

4. Подставив значения ииз (257) и (258) в равенство (256), получим с учетом данных задачи:

. (259)

Тогда уравнение (255), где , примет вид

. (260)

Постоянную интегрирования определяем по начальным условиям: при ,. Получим. При этом значениииз уравнения (260) находим искомую зависимостьот:

. (261)

Ответ: с^–1, где – в секундах.

Пример 10. Механическая система (рис. 58) состоит из сплошного однородного цилиндрического катка 1, подвижного блока 2, ступенчатого шкива 3 с радиусами ступеней ии радиусом инерции относительно оси вращения, блока 4 и груза 5 (коэффициент трения груза о плоскость равен). Тела системы соединены нитями, намотанными на шкив 3. К центрублока 2 прикреплена пружина с коэффициентом жесткости; ее начальная деформация равна нулю. Система приходит в движение из состояния покоя под действием силы , зависящей от перемещения точки ее приложения. На шкив 3 при движении действует постоянный моментсил сопротивления.

Д

Рис. 58

ано: кг,кг,кг,кг,кг,м,м,м,,Н/м,,Н,м.

Определить: в тот момент времени, когда.

Решение:

1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 3, 5 и невесомых тел 2, 4, соединенных нитями. Изобразим действующие на систему внешние силы: активные ,, , , , реакции , , , , натяжение нити , силы трения,и момент.

Для определения воспользуемся теоремой об изменении кинетической энергии:

. (262)

2. Определяем и . Так как в начальный момент система находилась в покое, то . Величина равна сумме энергий всех тел системы:

. (263)

Учитывая, что тело 1 движется плоскопараллельно, тело 5 – поступательно, а тело 3 вращается вокруг неподвижной оси, получим

,

,

, (264)

Все входящие сюда скорости надо выразить через искомую . Для этого предварительно заметим, что, где– любая точка обода радиусашкива 3 и что точка– мгновенный центр скоростей катка 1, радиус которого обозначим. Тогда

, . (265)

Кроме того, входящие в (3) моменты инерции имеют значения

, . (266)

Подставив все величины (265) и (266) в равенства (264), а затем, используя равенство (263), получим окончательно

. (267)

3. Найдем сумму работ всех действующих внешних сил при перемещении, которое будет иметь система, когда центр катка 1 пройдет путь . Введя обозначения:– перемещение груза 5 (),– угол поворота шкива 3,и– начальное и конечное удлинения пружины, получим

,

,

,

,

.

Работы остальных сил равны нулю, т.к. точки и, где приложены силы , и– мгновенные центры скоростей; точки, где приложены силы , и – неподвижны; а сила – перпендикулярна перемещению груза.

По условиям задачи,. Тогда, где– перемещение точки(конца пружины). Величиныинадо выразить через заданное перемещение. Для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Тогда, так как(равенствоуже отмечалось), то и.

И

Рис. 59

з рис. 59 видно, что , а так как точка является мгновенным центром скоростей для блока 2 (он как бы «катится» по участку нити ), то ; следовательно, и . При найденных значениях идля суммы вычисленных работ получим

. (268)

Подставляя выражения (267) и (268) в уравнение (262) и учитывая, что , придем к равенству

. (269)

Из равенства (269), подставив в него числовые значения заданных величин, найдем искомую угловую скорость .

Ответ: с^–1.

Пример 11. Механическая система (рис. 60) состоит из обмотанных нитями блока 1 радиуса и ступенчатого шкива 2 (радиусы ступенейи, радиус инерции относительно оси вращения), и из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом, приложенной к блоку 1.

Дано: Н,Н,Н,Н,,м,м,м;м.

Определить: ускорение груза 3, пренебрегая трением.

Рис. 60

Решение:

1. Рассмотрим движение механической системы, состоящей из тел 1, 2, 3, 4, соединенных нитями. Система имеет одну степень свободы. Связи, наложенные на эту систему, – идеальные.

Для определения применим общее уравнение динамики:

, (270)

где – сумма элементарных работ активных сил;– сумма элементарных работ сил инерции.

2. Изображаем на чертеже активные силы ,,и пару сил с моментом. Сообщим системе возможное перемещениеи составим выражение для суммы работ:

.

Выразим через:

.

В результате получим

. (271)

3. Задавшись направлением ускорения , изображаем на чертеже силы инерции , и пару сил инерции с моментом , величины которых равны:

, , . (272)

Сообщая системе возможное перемещение , получим:

. (273)

Выразим все ускорения, входящие в (272) через искомую величину

, ,

а перемещения через :

, , .

В результате получим:

. (274)

Подставив величины и (формулы (271) и (274)) в уравнение (270), и сократив на , найдем:

. (275)

Вычисления дают м/с². Знак указывает, что ускорение груза 3 и ускорения других тел направлены противоположно показанным на рис. 60.

Ответ: м/с², ускорение груза 3 и ускорения других тел направлены противоположно показанным на рисунке.

Пример 12.

Механическая система (рис. 60) состоит из обмотанных нитями блока 1 радиуса и ступенчатого шкива 2 (радиусы ступенейи, радиус инерции относительно оси вращения), и из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом, приложенной к блоку 1.

Дано: Н,Н,Н,Н,,м,м,м;м.

Определить: ускорение груза 3, пренебрегая трением.

Решение:

1. Система имеет одну степень свободы. Выберем в качестве обобщенной координаты перемещение груза 3, полагая, что он движется вниз и отсчитываяв сторону движения (рис. 60). Составим уравнение Лагранжа:

. (276)

2. Определим кинетическую энергию всей системы, равную сумме кинетических энергий всех тел:

. (277)

Грузы 3 и 4 движутся поступательно, поэтому шкив 2 вращается вокруг неподвижной оси, следовательно

, ,. (278)

Скорости ,ивыразим через обобщенную скорость:

, ,. (279)

Подставляя значения величин (279) в равенства (278), а затем значения ,ив соотношение (277), получим:

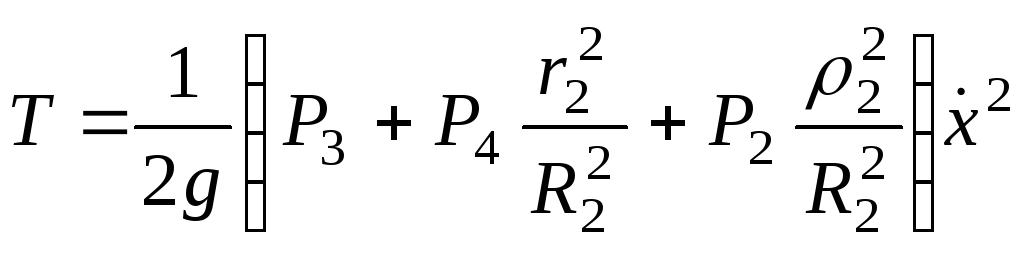. (280)

Так как кинетическая энергия зависит только от , производные левой части уравнения (276) примут вид:

,

, . (281)

3. Найдем обобщенную силу . Для этого составим уравнение работ активных сил на перемещении.Воспользуемся соотношением (271) примера 11:

. (282)

.

Коэффициент при в (282) и будет обобщенной силой:

. (283)

Подставляя (281) и (283) в уравнение (276), получим

.

Отсюда находим

м/с²,

что совпадает с ответом примера 11.

Ответ: м/с², что ускорение груза 3 и ускорения других тел направлены противоположно показанным на рисунке.