Векторный момент силы относительно точки

В

Рис. 2

екторным моментом силы относительно точки называют вектор, приложенный в этой точке и равный по модулю произведению силы на плечо силы относительно этой точки. Векторный момент силы направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть стремление силы вращать тело против движения часовой стрелки (рис. 2). Согласно определению,

.

Справедлива формула

, (2)

где – радиус-вектор, проведенный из моментной точкив точку приложения силы или любую другую точку линии действия силы.

Е

Рис. 3

сли силадана своими проекциямина оси координат и даны координатыточки приложения этой силы (рис. 3), то векторный момент относительно начала координат, согласно формуле (9), после разложения по осям координат вычисляется по формуле

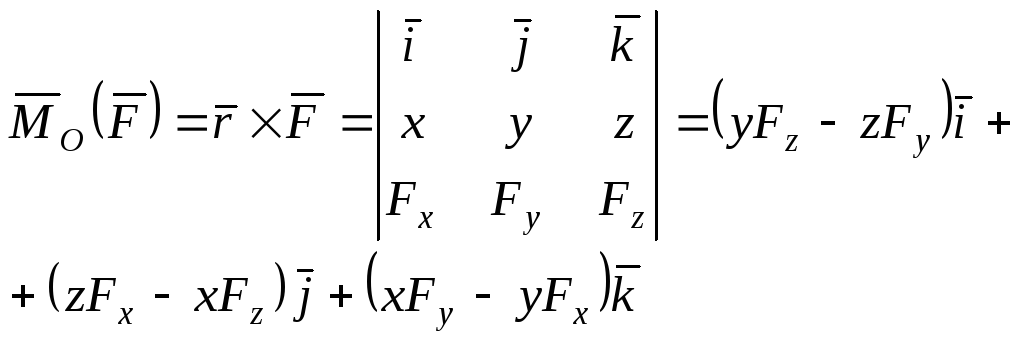, (3)

где – единичные векторы, направленные по осям координат, т.е. орты данной системы.

Используя формулу (3), можно выделить проекции на оси координат:

(4)

Момент силы относительно оси

Моментом силы относительно оси называют алгебраический момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью (рис. 4). Момент силы относительно оси считается положительным, если проекция силы на плоскость, перпендикулярную оси (проекция силы на плоскость является вектором), стремится вращать тело вокруг положительного направления оси против часовой стрелки, и отрицательным, если она стремится вращать тело по часовой стрелке. Момент силы, например, относительно оси обозначим. По определению,

,

г

Рис. 4

де– вектор проекции силына плоскость, перпендикулярную оси, а точка– точка пересечения осис плоскостью.

Момент силы относительно оси равен нулю, если сила параллельна оси (в этом случае равна нулю проекция силы на плоскость, перпендикулярную оси); если линия действия силы пересекает эту ось (в этом случае линия действия проекции силы на плоскость, перпендикулярную оси, проходит через точку пересечения оси с плоскостью, соответственно, равно нулю плечо силы относительно точки).

Связь между моментом силы относительно оси и векторными моментами силы относительно точек, лежащих на этой оси: момент силы относительно оси равен проекции на эту ось векторного момента силы относительно любой точки на оси.

Используя эту связь можно вычислить моменты силы относительно прямоугольных осей координат:

. (5)

1.1.2. Пара сил Пара сил и алгебраический момент пары сил

П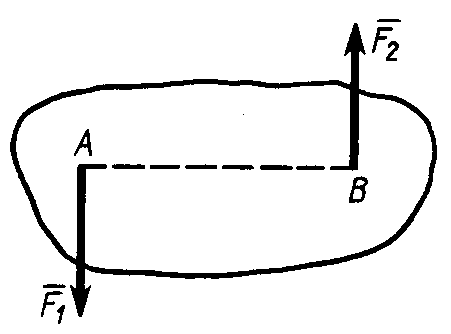арой сил называют систему двух равных по модулю параллельных сил, направленных в противоположные стороны (рис. 5).

Плоскостью действия пары сил называют плоскость, в которой расположены силы пары.

А

Рис. 5

лгебраическим моментом пары сил называют взятое со знаком плюс или минус произведение одной из сил пары на плечо пары сил.

Плечом пары сил называют кратчайшее расстояние между линиями действия сил пары.

Алгебраический момент пары обозначим или. Согласно определению,

. (6)

Алгебраический момент пары сил имеет знак плюс, если пара сил стремится вращать тело против часовой стрелки, и знак минус, если пара сил стремится вращать тело по часовой стрелке.

Две пары сил называют эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.

Теорема об эквивалентности двух пар сил: пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющей одинаковый с первой парой алгебраический момент.

Следствия теоремы:

а) пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия;

б) у пары сил можно изменять плечо и силы, сохраняя при этом алгебраический момент пары и плоскость действия.

Теорема об эквивалентности двух пар сил, расположенных в одной плоскости: действие пары сил на твердое тело не изменяется от переноса этой пары сил в параллельную плоскость.

В

Рис. 6

екторным моментом пары сил назовем вектор, числовое значение которого равно произведению силы пары на ее плечо. Векторный момент пары сил направлен перпендикулярно плоскости действия пары сил так, чтобы с его направления можно было видеть стремление пары сил вращать тело против часовой стрелки (рис. 6).

,

где – плечо пары сил.

Теорема об эквивалентности пар сил: две пары сил, действующие на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению векторные моменты.

Теорема о сумме моментов сил пары сумма векторных моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора точки и равна векторному моменту этой пары сил, т.е. для пары сил

, (7)

где – любая точка.

Теорема о сложении пар: две пары сил, действующие на одно и то же тело и лежащие в пересекающихся плоскостях, можно заменить одной эквивалентной парой сил, векторный момент которой равен сумме векторных моментов заданных пар сил.

Для пар сил, расположенных в одной плоскости, теорема об их сложении формулируется так: пары сил, действующие на твердое тело и расположенные в одной плоскости, можно привести к одной паре сил, алгебраический момент которой равен сумме алгебраических моментов составляющих пар сил, т. е.

. (8)