3.3.2. Моменты инерции Моменты инерции относительно точки и оси

Моментом инерции механической системы, состоящей изматериальных точек, относительно точкиназывается сумма произведений масс этих точек на квадраты их расстояний до точки(рис. 51), т. е.

. (139)

М

Рис. 51

омент инерции относительно точки часто называютполярным моментом инерции. В случае сплошного тела сумма переходит в интеграл и для полярного момента инерции имеем:

, (139')

где – масса элементарной частицы тела (в пределе точка);– ее расстояние до точки.

Моментом инерции системы материальных точек относительно осиназывается сумма произведений масс этих точек на квадраты их расстоянийдо оси(рис. 51):

. (140')

В частном случае сплошного тела сумму следует заменить интегралом:

, (140')

Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции. Радиус инерции , относительно осиопределяется но формуле

, (141)

где – масса тела.

Момент инерции относительно оси через радиус инерции относительно этой оси определяется выражением

, (141')

В справочниках по моментам инерции приводят таблицы значений радиусов инерции различных тел.

Моменты инерции относительно осей координат

Моменты инерции относительно декартовых осей координат ,ии их начала – точки(рис. 52) – определяются выражениями:

,

,

, (142)

, (143)

где – координаты материальных точек системы. Для сплошных тел эти формулы примут вид

, ,

, .

С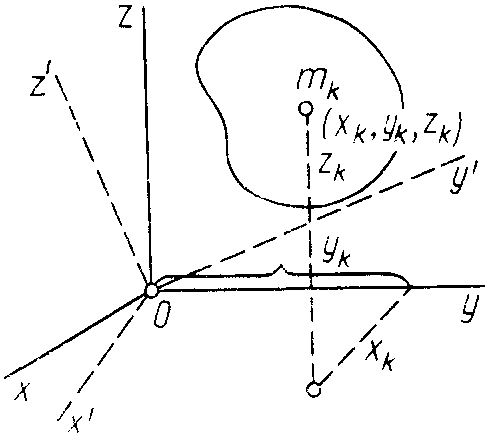умма моментов инерции относительно декартовых осей координат не зависит от ориентации этих осей в рассматриваемой точке, т.е. является величиной, инвариантной по отношению к направлению осей координат.

Д

Рис. 52

ля осей координатможно определить следующиетри центробежных момента инерции:

, ,. (144)

Центробежные моменты инерции часто называют произведениями инерции. Если центробежные моменты инерции равны нулю, оси называют главными осями инерции. Если при этом в качестве начала координат выбран центр масс, их называют главными центральными осями инерции

Моменты инерции относительно осей и точек – величины положительные. Центробежные моменты инерции могут быть как положительными, так и отрицательными.

Кроме рассмотренных моментов инерции иногда используются моменты инерции относительно координатных плоскостей ,,:

, ,.

3.3.3. Теорема Штейнера

У

Рис. 53

становим зависимость между моментами инерции системы относительно параллельных осей, одна из которых проходит через центр масс. Пусть имеем две системы прямоугольных, взаимно параллельных осей координати. Начало системы координатнаходится в центре масс системы (рис. 53).

По определению момента инерции относительно оси имеем:

, ,

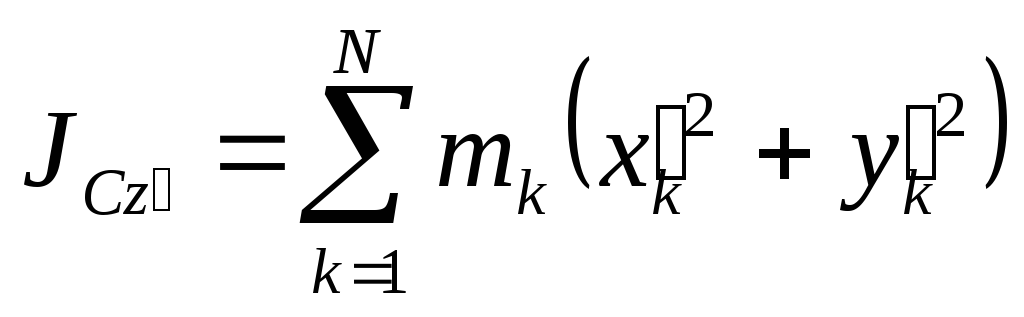где – масса точки, аи– координаты этой точки относительно системи. Обозначим расстояние между осямиичерез.

Связь моментов инерции относительно двух параллельных осей, одна из которых проходит через центр масс, составляет содержание так называемой теоремы Штейнера или Гюйгенса–Штейнера: момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями:

. (145)