2.1.1. Скорость и ускорение точки

Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета, которая изображена в виде декартовой прямоугольной системы координат (рис. 21).

П

Рис. 21

оложение движущейся точкиотносительно рассматриваемой системы отсчета определяется в момент временирадиусом-вектором, который соединяет неподвижную точкус этой точкой. В другой момент временидвижущаяся точка займет положениеи ее радиусом-вектором будет. За времярадиус-вектор движущейся точки изменится на.

Средней скоростью точки за времяназывают отношение, т.е.:

.

Средняя скорость параллельна вектору . В общем случае она зависит от времени осреднения. У нее нет конкретной точки приложения на траектории.

Введем скорость точки в момент, которая определяется как предел средней скорости, если промежуток времени, за который определяется средняя скорость, стремится к нулю, т. е.

.

Скорость точки направлена в сторону ее движения по предельному направлению вектора при, стремящемся к нулю, т.е. по предельному направлению секущей, которая совпадает с касательной к траектории в точке. Таким образом, скорость точки равна первой производной по времени от ее радиуса-вектора. Она направлена по касательной к траектории в сторону движения точки.

Начало радиуса-вектора движущейся точки можно выбрать в любой неподвижной точке. На рис. 21 представлен случай, в котором радиусом-вектором является также с началом в точке. Радиусы-векторы имеют одинаковые измененияиза времяи поэтому

. (44)

Пусть движущаяся точка в момент времениимеет скорость. В момент времениэта точка занимает положение, имея скорость(рис. 22). Чтобы изобразить приращение скоростиза время, перенесем вектор скоростипараллельно самому себе в точку.

С

Рис. 22

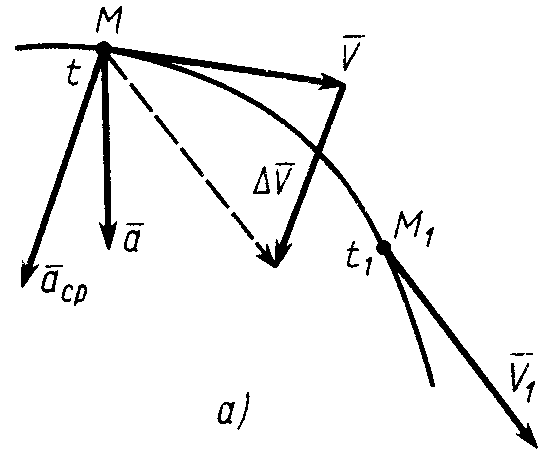
редним ускорением точки за времяназывают отношение, т.е.. Среднее ускорение точки параллельно приращению скорости. Как и средняя скорость, среднее ускорение не имеет на траектории конкретной т

ечки приложения и изображено в точкеусловно. В общем случае среднее ускорение зависит от времени.

Ускорением точки в момент времениназывают предел, к которому стремится среднее ускорение при, стремящемся к нулю, т. е.

. (45)

Таким образом, ускорение точки равно первой производной по времени от скорости точки.

Приращение скорости и, следовательно, среднее ускорение направлены внутрь вогнутости траектории. Так же направлены и их предельные значения при, стремящемся к нулю. Поэтому ускорение точки направлено тоже внутрь вогнутости траектории.

Ускорение точки можно представить в виде (рис. 23):

. (46)

Часть ускорения, равная

Рис. 23

,

называется касательной составляющей ускорения. Она направлена по касательной к траектории. Другая часть ускорения

называется нормальной составляющей ускорения (– радиус кривизны траектории). Она направлена внутрь вогнутости траектории, перпендикулярно.

2.1.2. Векторный способ задания движения точки

Д

Рис. 24

вижение точки относительно рассматриваемой системы отсчета при векторном способе изучения движения задается радиусом-векторомэтой точки (рис. 24). Движение точки считается заданным, если известен радиус-вектор движущейся точки как функция времени, т. е.

. (47)

Задание векторного уравнения движения (47) полностью определяет движение точки.

Скорость точки направлена по касательной к траектории и вычисляется, согласно ее определению, по формуле:

. (48)

Для ускорения точки соответственно имеем

. (49)

Определение скорости и ускорения точки сводится к чисто математической задаче вычисления первой и второй производных по времени от радиуса-вектора этой точки.