Метод эквивалентных преобразований

Две ветви, не содержащие источников и подключенные к одной и той же паре узлов, представляют собой параллельное соединение и могут быть заменены одной эквивалентной ветвью. При этом ток в ветви, которая не преобразуется, остается неизменным.

Заменяем сопротивления Z₁иZ₂ (рис. 2.4) эквивалентным сопротивлениемZ₁₂:

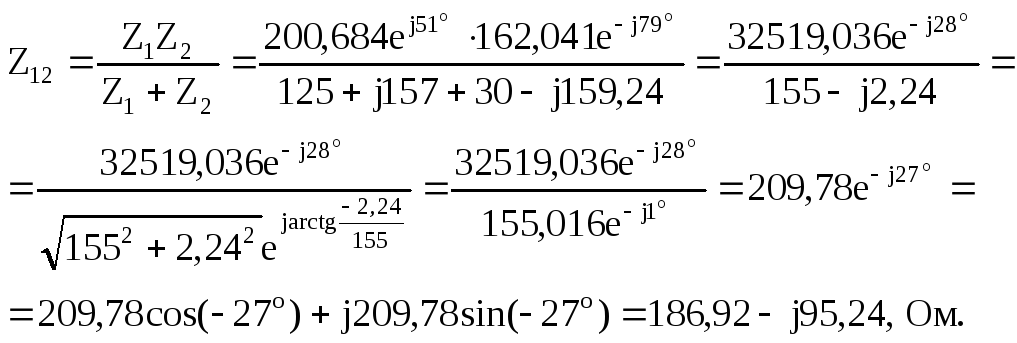
Тогда схема рис. 2.4 может быть представлена эквивалентной схемой (рис.2.5), в которой через все элементы схемы протекает один и тот же ток İ₃. Точки 1 и 2 перестали быть узлами, но напряжение между ними осталось одно и тоже.

Рис. 2.5

Согласно закону Ома для участка 12схемы рис.2.5

Комплексные действующие значения токов параллельно соединенных ветвей (рис.2.4) записываем, используя закон Ома для каждой ветви в отдельности:

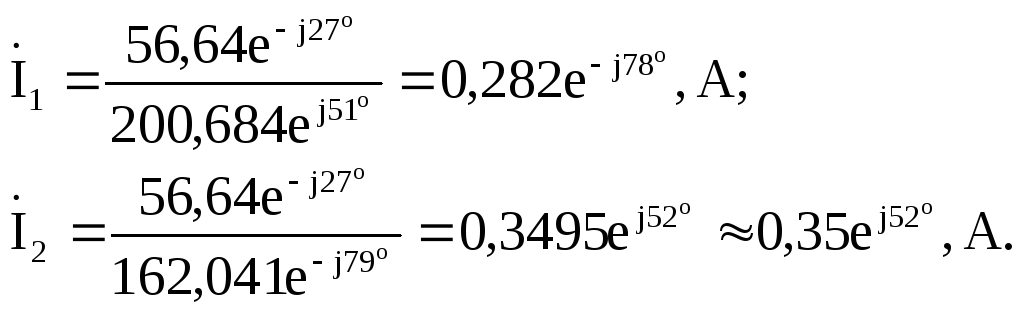
Правило пропорции

Существует пропорция между током в одной из параллельно соединенных ветвей и током в ветви с источником.

На примере схемы рис 2.4, подставив выражения для напряжения U₁₂и эквивалентного сопротивления участкаZ₁₂в закон Ома для второй ветви (рис. 2.5), получаем:

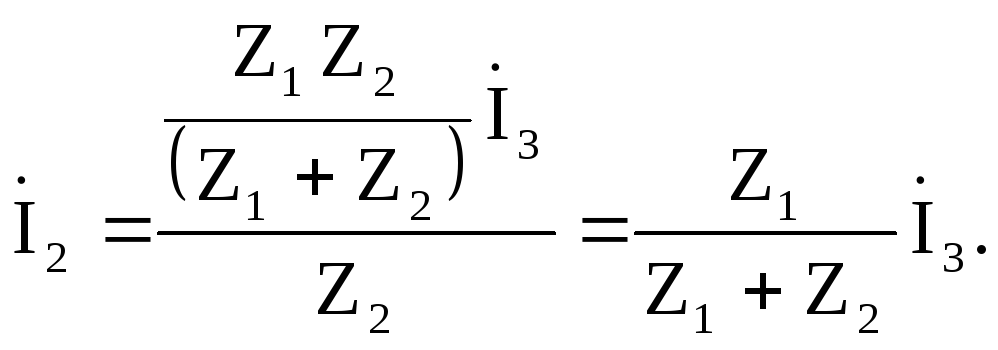
6. Определение ЭДС источника.

Для схем рис. 2.3, 2.4, 2.5 ЭДС источника может быть найдена согласно второму закону Кирхгофа как алгебраическая сумма напряжений на приемниках, образующих замкнутый контур с источником ЭДС.

Например, для схемы рис. 2.5 комплексное действующее значение ЭДС равно:

или

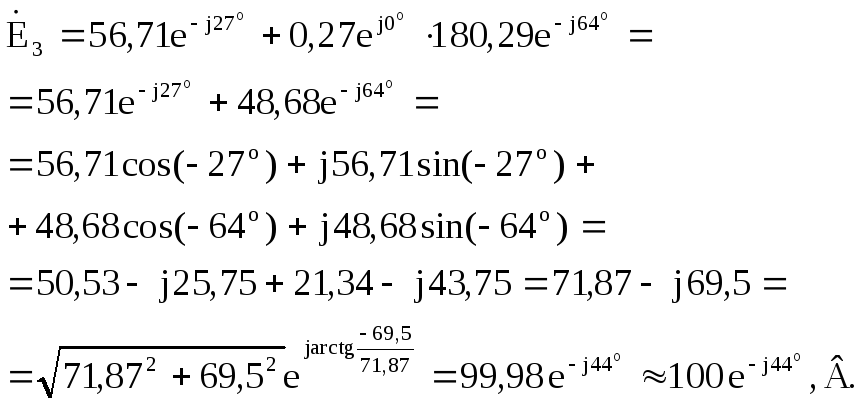
Рассчитываем напряжения на каждом из приемников рассматриваемой схемы.

Для схемы рис. 2.3:

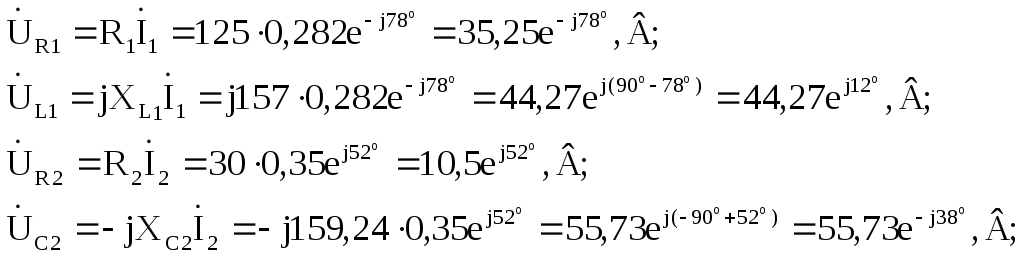
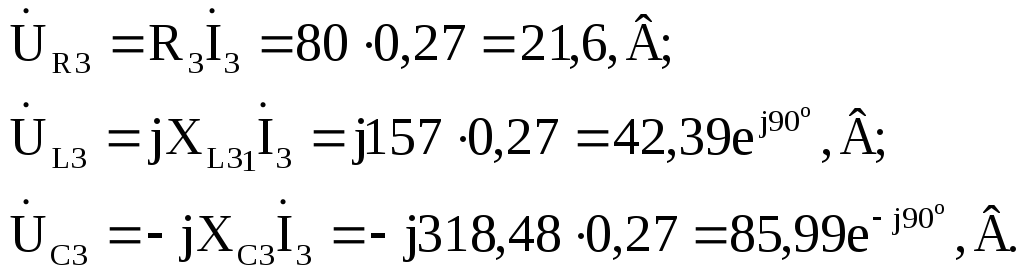
7. Построение векторной диаграммы.

Векторной диаграммойназываетсясовокупность векторов токов, напряжений и ЭДС, изображающих синусоидальные электрические величины цепи в момент времениt=0. Векторная диаграмма цепи образуется векторными диаграммами ее ветвей, которые в свою очередь состоят из отдельных диаграмм элементов цепи.

Все построения выполняются на одной комплексной плоскости с осями координат (+1), (+j). Начало вектора совмещают с началом координат. Длины векторов пропорциональны действующим значениям электрических величин, а направления векторов определяются их начальными фазами. Положительные углы откладываются от оси (+1) против движения часовой стрелки, а отрицательные - по направлению движения.

Для построения векторной диаграммы необходимо выбрать масштабы по току и напряжению таким образом, чтобы векторная диаграмма занимала не менее половины страницы.

Построение начинают с любого вектора.

Для схемы рис. 2.3 вектор тока İ₁ проведем из начала координат под углом 78^о, повернув его по ходу часовой стрелки (ψ_i1<0) относительно оси (+1), а вектор тока İ₂- под углом 52^о, повернув его против движения часовой стрелки (ψ_i2>0) (рис. 2.6). Аналогично строим вектор тока İ₃, вектора напряжений на всех приемниках и вектор ЭДС.

Затем в соответствии с выражениями:

,

складываем векторы напряжений элементов первой и второй ветвей, для чего из конца первого вектора напряжения проводим второй вектор напряжения. Вектор, соединяющий начало первого вектора и конец второго, равен вектору напряжения между узлами 1, 2схемы рис. 2.3 (рис. 2.6).

Далее получаем напряжение участка, содержащего приемники третьей ветви: . Результирующая векторная диаграмма приведена на рис. 2.6.

Проверку правильности расчетов и построения векторов. начинаем с проверки векторных диаграмм элементов. Так, вектор напряжения на участке с резисторомдолжен совпасть по направлению с вектором тока. Вектор напряжения на участке с индуктивным элементомдолжно быть сдвинутпротивхода часовой стрелки на угол 90^о относительно вектора тока, а вектор напряжения на участке с емкостным элементомдолжен быть сдвинутпонаправлению движения часовой стрелки на 90^оотносительно вектора тока. Далее на рис. 2.6 складываем векторы токов İ₁ и İ₂. Если , то первый закон Кирхгофа выполняется. Если при суммировании векторов напряжений вдоль независимых контуров, выполняется, например, условие, то второй закон Кирхгофа тоже сходится.

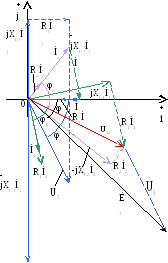
Рис.2.6

Указываем на диаграмме угол сдвига фаз для каждой из ветвей и всей цепи. Угол φ отсчитывается в направлении от вектора тока к вектору напряжения и равен аргументу комплексного сопротивления ветви. φ положителен при отстающем токе и отрицателен при опережающем токе.

8. Построение временных зависимостей. С этой целью переходим от рассчитанных в комплексной форме электрических величин к их мгновенным значениям.

Изображение временных характеристик основано на построении периодической функции времени с периодом T=1/f.

Временные зависимости синусоидальных функций могут быть построены с помощью существующих компьютерных программ или вручную, как это показано на примере тока первой ветви и напряжения участка 12 схемы рис. 2.2.

В прямоугольной системе координат по оси абсцисс откладываем в масштабе время (или пропорциональная ему величина ωt), а по оси ординат значения тока, соответствующие выбранному моменту времени. Масштаб по времени и по току должен быть таким, чтобы график занимал на менее половины страницы.

Для удобства построения выбираем исчисление периода в электрических градусах (T=360⁰).

• От начала координат откладываем начальную фазу тока ψ: влево - при ψ>0, вправо - при ψ<0. Полученная точка 1является началом графика.

• Для построения точек 2и3вдоль оси времени вправо и влево от точки 1 откладываем отрезки, равные половине периода (180^о) и периоду (360^о) и отмечаем нулевые значения синусоиды.

• В точках 4и5отмечаем максимальные значения синусоиды, откладывая вправо и влево от точки 1 вдоль оси ωt отрезки, равные ¼ периода (90^о) и ¾ периода (270^о).

• В дополнительных точках 6, 7, 8, 9отмечаем половину амплитудного значения тока. Соответствующие им моменты времени расположены вдоль оси времени на удалении 1/12 периода (30^о) влево и вправо от точек1, 2, 3.

Графики тока i₁и напряженияu₁₂cтроим на одной плоскости, показываем их начальные фазы и угол сдвига фаз между ними (рис. 2.7).

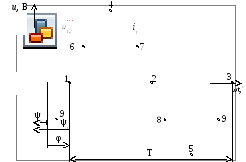
Рис. 2.7

9. Расчет мощности цепи однофазного синусоидального тока.

Мощность источника цепи в символическом виде определяется произведением комплекса напряжения или ЭДС источника и сопряженного комплекса тока в соответствующей ветви, т.е.

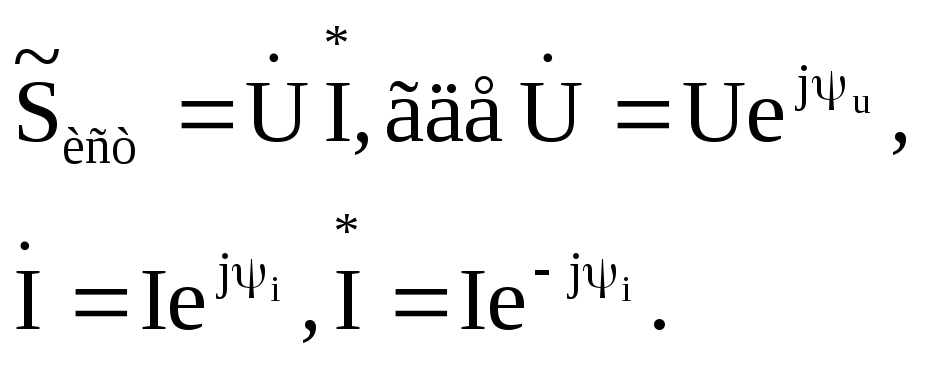
В этом выражении величина cosφназывается коэффициентом мощности цепи переменного тока.

Мощность приемников определяется как произведение квадрата действующего значения тока на комплексное сопротивление элемента:

Баланс мощностей определяется уравнением

илиP_ист=P_пр,Q_ист=Q_пр

Сравниваются результаты вычислений левой и правой части равенства. Погрешность расчетов не должна превышать 3 %.