Лабораторная работа № 2

Цель работы № 2: экспериментальное определение токов в ветвях сложной электрической цепи постоянного тока методом наложения.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Метод наложения

Принцип наложения формулируется следующим образом: ток в k-той ветви любой сложной линейной электрической цепи равен алгебраической сумме токов, вызываемой каждой ЭДС в отдельности. Принцип наложения и соответствующий ему метод расчета (метод наложения) вытекают из свойства линейности электрической цепи.

Чтобы рассчитать токи методом наложения, представим схему (рис. 2.1, а) в виде двух схем (рис. 2.1, б, в), оставив в каждой схеме только по одному источнику ЭДС. Определяем частичные токи I₁', I₂', I₃' от действия первого источника ЭДС E₁ (рис. 2.1, а) и токи I₁'', I₂'', I₃'' от действия второго источника ЭДС E₂ (рис. 2.1, б) с помощью метода свертывания. Действительные токи находим из алгебраической суммы частичных токов: I₁ = I₁' – I₁''; I₂ = I₂' - I₂''; I₃ = I₃' + I₃''.

Рис.2.1

Вспомогательные приемы

Для облегчения и упрощения решения сложных уравнений используется ряд вспомогательных приемов, например,таких как эквивалентные преобразования расчетных схем.

Эквивалентным называется такое преобразование, при которомтоки и напряжения в частях схемы, не затронутых преобразованием, остаются неизменными. Рассмотрим некоторые из них.

Последовательнымсоединением элементов электрической цепи называют такое соединение, при котором через все элементы протекает один и тот же ток (рис. 2.2, а).

Для этой схемы согласно второму закону Кирхгофа

76

где общее сопротивление цепи (рис. 2.2, б), равное сумме значений последовательно включенных сопротивлений:

При параллельном соединении элементы электрической схемы подсоединены к одной и той же паре узлов и находятся под одним и тем же напряжением (рис. 2.3, а).

В этом случае согласно первому закону Кирхгофа:

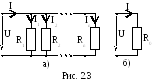
Эквивалентное значение (рис. 2.3, б) параллельно соединенных сопротивлений определяется из соотношения

Последнее выражение можно записать как

- суммарная проводимостьпараллельно соединенных элементов равна сумме их проводимостей.

Для частного случая двух параллельно соединенных сопротивлений

При смешанномсоединении элементов цепи их эквивалентные сопротивления находят, применяя указанные выше расчеты комбинированно. Покажем это на следующих двух примерах (рис. 2.4, а, б).

Для схемы рис. 1.9, а

Всхеме рис. 2.4, б, сначала определяют сопротивление каждой ветвизатем находят проводимость схемы между точкамиaиbкак сумму проводимостей всех ветвей

,

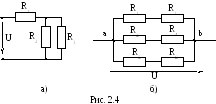
Зная сопротивление между любыми точками в схеме и напряжение, подведенное к ним, нетрудно подсчитать токи в каждой ветви схемы и распределение напряжения в ней.

На рис. 2.5 показано соединение трех сопротивлений, называемое соединением треугольники соединениемзвезда.

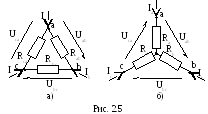
При расчете электрических цепей довольно часто оказывается полезным преобразовать треугольник в эквивалентную заезду или наоборот, звезду в треугольник. Согласно условию эквивалентности токи и напряжения в частях схемы, не затронутых преобразованием, остаются неизменными. Это означает, что токи и напряженияв схемах треугольника и звезды одинаковы.

Условие эквивалентности должно быть соблюдено во всех режимах, в том числе и при обрыве одного из линейных проводов. При обрыве линейного провода, присоединенного к узлу напряжениеи токииодинаковы для схем треугольника и звезды. Следовательно, сопротивления между узламиbитакже одинаковы для двух схем. Аналогичная ситуация создается при обрыве линейных проводов с токами I_b и I_c. Для всех трёх случаев:

обрыв провода ;

обрыв провода ;

обрыв провода .

В этой системе уравнений всегда три сопротивления заданы, три неизвестны.

Решая систему уравнений относительно неизвестных сопротивлений звездыпри заданных сопротивлениях треугольника, имеем:

для сопротивлений треугольникапри замене сопротивлений звезды

78

Рассмотрим полезность подобных преобразований на следующем примере (рис. 2.6, а, б).

80

В схеме рис. 2.6, а нет ни последовательно, ни параллельно соединенных сопротивлений.

Если треугольник из R₁, R₂, R₅заменить эквивалентной звездой с сопротивлениями R_a, R_bи R_c, то схема становится простой со смешанным соединением сопротивлений.

Рис. 2.6

ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

В работе исследуется электрическая цепь с двумя источниками энергии (E₂, E₃) и тремя нагрузочными резисторами (R₁, R₂, R₃), установленными в блоках стенда (рис. 2.7).

Паспортные данные источников определены экспериментально в лабораторной работе № 1.

Параметры приемников с погрешностью ±10 % указаны на панели стенда. Точное значение сопротивлений определено экспериментальным способом в лабораторной работе № 1.

Измерительные приборы: три амперметра типа Э59 0,25÷1,0 А; цифровой вольтметр – 1 шт.

Рис. 2.7

Подготовка к выполнению работы

1. Изучить по учебнику, конспекту лекций раздел «Линейные электрические цепи постоянного тока».

2. Ознакомиться по данному пособию с программой выполнения работы.

3. Подготовить бланк отчета по выполнению лабораторной работы.

4. Произвести расчет токов в ветвях схемы замещения цепи лабораторной работы (рис. 2.7) методом наложения. Значения ЭДС E₂ и E₃, их внутренних сопротивлений и сопротивлений приемников взять из данных лабораторной работы № 1. Выполнить проверку правильности расчетов токов в ветвях схемы замещения с помощью законов Кирхгофа. Данные расчета занести в табл. 2.1 (колонки «расчет схемы замещения»).

Программа выполнения работы

1. Собрать электрическую цепь (рис. 2.7).

2. Измерить частичные токи в ветвях цепи от действия источника E₂. Для этого переключатель П₂ перевести в положение «b», а переключатель П₃ - в положение «a». Данные измерений занести в табл. 2.1. Выполнить проверку соответствия экспериментальных данных первому закону Кирхгофа.

3. Измерить токи в ветвях от действия источника E₃. Для этого переключатель П₂ перевести в положение «a», а переключатель П₃ - в положение «b». Данные измерений занести в табл. 2.1. Выполнить проверку соответствия экспериментальных данных первому закону Кирхгофа.

4. Вычислить действительные токи в ветвях цепи, используя метод наложения и экспериментальные данные табл. 2.1. Данные вычислений занести в колонки «вычислено» в табл. 2.1.

5. Сравнить действительные токи, полученные методом наложения из табл. 2.1 лабораторной работы № 2 с измеренными действительными токами лабораторной работы № 1 (табл. 1.1). Сделать выводы.

Таблица 2.1

I1',А

I2',А

I3',А

I1'',А

I2'',А

I3'',А

I1,А

I2,А

I3,А

Измерено

Вычислено

Расчет схемы замещения

6. Сравнить экспериментальные данные с расчетными токами схемы замещения из табл. 2.1. Сделать выводы по работе.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Поясните полученные в работе результаты и сделанные выводы.

2. Что Вы понимаете под эквивалентным сопротивлением электрической цепи и эквивалентными источниками электрической энергии.

3. Напишите выражения и поясните их вывод для замены последовательного и параллельного соединения сопротивлений эквивалентным сопротивлением.

4. Напишите выражения и поясните их вывод для эквивалентного преобразования соединения в виде треугольника в соединение типа “звезда” и обратно.

5. Расскажите про эквивалентную замену последовательно включенных источников ЭДС.

6. Какие алгоритмы и методы расчета электрических цепей Вы знаете? Что понимают под “расчетом электрических цепей”?

7. Расскажите про принцип наложения и методику его использования для расчета электрических цепей.

8. Поясните название “частичные токи”. Как они определяются при использовании метода наложения?

9. Какие величины измеряются в цепи лабораторной работы при переключении переключателей П₂ и П₃ в среднее положение, положение «а» и «b»?

Лабораторная работа № 3

ИССЛЕДОВАНИЕ

РЕЖИМОВ РАБОТЫ ПРИЕМНИКОВ

ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА

Цель работы: экспериментальное определение параметров пассивных элементов электрической цепи; исследование влияния переменного параметра (емкости С) на величины тока и напряжений в неразветвленной цепи, исследование режима резонанса напряжений.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Цепи синусоидального тока. Основные определения

Переменные электрические величины являются функциями времени, их значения в любой момент времени t называют мгновенными и обозначают строчными буквами.

Мгновенное значение синусоидального тока определяется выражением

,

где I_m – амплитудное значение тока;

(ωt+ ψ_i) – фаза, измеряемая в радианах и градусах;

ψ_i – начальная фаза в радианах (или электрических градусах);

ω – угловая частота в рад/с, ,

где T – период с секундах.

f – частота изменения тока определяется количеством периодов в секунду: f [Гц] =1/ T. Очевидно, что ω=2π f.

График мгновенных значений тока (волновая диаграмма) показан на рис. 3.1.

ψ_i– начальная фаза тока отсчитываются от начала синусоиды (точки перехода синусоидальной функции через ноль от отрицательных к положительным ее значениям) до начала отсчета времени (рис. 3.1).

Начальная фаза может быть, положительной, отрицательной и равной нулю. При ψ > 0 начало синусоиды сдвинуто влево относительно начала координат, при ψ < 0 – вправо, а при ψ = 0 синусоида имеет начало в начале координат.

Рис. 3.1

Все сказанное относительно тока справедливо также для синусоидально изменяющихся напряжений u(t) и ЭДСe(t).

На рис. 3.2 представлены волновые диаграммы ЭДС, тока и напряжения одинаковой частоты:

e(t) = E_m sin(ωt +ψ_e),

u(t) = U_m sin(ωt +ψ_u),

i(t) = I_m sin(ωt +ψ_i).

Угол, на который синусоида тока сдвинута относительно синусоиды напряжения, называют углом сдвига фаз φ и определяют его как разность начальных фаз напряжения и тока:

φ=ψ_u - ψ_i.

Угол сдвига фаз на волновой диаграмме показывается стрелкой, направленной от графика напряжения к графику тока (рис. 3.2).

Большинство измерительных приборов измеряют действующие значения ЭДС, напряжений и токов, поэтому расчеты в цепях синусоидального тока чаще всего выполняются по действующим значениям, которые связаны с амплитудными следующими соотношениями:;;.

Рис. 3.2