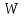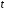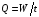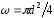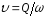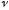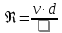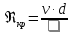Лаб раб 3 - Гидравлика, Ч.1 - Рейнольдс
.docx
Работа 1.3. Экспериментальное исследование ламинарного и турбулентного режимов движения жидкости, определение числа Рейнольдса и законов сопротивления
Цель работы:
-
Экспериментально убедиться в существовании ламинарного и турбулентного режимов течения путём окрашивания струйки воды в стеклянной трубе.
-
Вычислить по результатам измерений числа Рейнольдса при ламинарном и турбулентною режимах, сравнить их с критическим, убедиться, что при ламинарном режиме
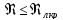 ,
а при турбулентном –
,
а при турбулентном –
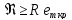 .
.
-
Рассчитать и построить график
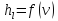 ,
определить с его помощью критическую
скорость
,
определить с его помощью критическую
скорость
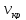 ,
а через нее вычислить критическое число
,
а через нее вычислить критическое число
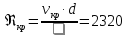 .
.
-
Подтвердить с помощью графика
 ,
что при ламинарном режиме потери напора
по длине
,
что при ламинарном режиме потери напора
по длине
 пропорциональны средней скорости в
первой степени, а при турбулентном - в
степени
пропорциональны средней скорости в
первой степени, а при турбулентном - в
степени
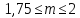 .
.
Краткие теоретические сведения.
Существуют два принципиально различных режима течения жидкости: ламинарный и турбулентный. Наличие двух режимов движения было экспериментально подтверждено в 1883 году английским физиком О.Рейнольдсом. Он наблюдал структуру ламинарного и турбулентного потоков визуально на простой установке (рис. 3.1).
К баку 1 подсоединена горизонтальная стеклянная труба 2 с краном 3. Над баком установлен сосуд 4 с окрашенной жидкостью, которая подаётся в трубу 2 по тонкой трубке 5, снабжённой краником 6. В бак 1 заливается вода, и уровень её поддерживается постоянным. Затем открытием крана 3 в трубе 2 создают поток, в который подают тонкую струйку окрашенной жидкости. Постепенным открытием крана 2 можно повышать расход, а, следовательно, и скорость жидкости в трубе.
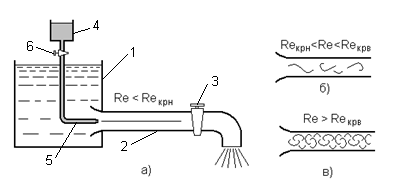
а) – ламинарный; б) – переходный; в) - турбулентный
Рисунок 3.1 - Режимы течения жидкости
Исследования показали, что при небольших скоростях течения жидкости наблюдается ламинарный режим. При этом окрашенные струйки жидкости не перемешиваются с потоком, т.е. при ламинарном режиме наблюдается плавное слоистое течение без поперечного перемешивания частиц и без пульсаций скоростей и давлений (рис. 3.1,а). При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, поперечные перемещения жидкости отсутствуют.
При увеличении скорости картина течения вначале не меняется, но затем при достижении определённой скорости наступает быстрое её изменение. Струйка краски на выходе начинает колебаться (рис. 3.1,в), затем размываться и перемешиваться с потоком жидкости. При этом становится заметным вихреобразование и вращательное движение жидкости. Течение становится турбулентным.
Турбулентным называется течение, сопровождающееся интенсивным перемешиванием частиц жидкости и вихреобразованием, что обуславливает пульсацию скоростей и давлений. При турбулентном течении движение отдельных частиц оказывается подобным хаотическому движению молекул газа.
О.Рейнольдс установил связь этих режимов с определёнными интервалами числовых значений критерия, который впоследствии был назван его именем
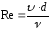 ,
(критерий Рейнольдса) (3.1)
,
(критерий Рейнольдса) (3.1)
где
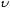 - средняя скорость движения жидкости;
- средняя скорость движения жидкости;
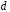 -
диаметр трубопровода;
-
диаметр трубопровода;
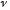 -
кинематическая вязкость жидкости.
-
кинематическая вязкость жидкости.
Средняя
скорость потока, при которой происходит
смена режима движения жидкости, называется
критической -
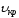 .
Величина ее, как показывают опыты в
трубопроводах круглого сечения, зависит
от рода жидкости, характеризуемого
динамической вязкостью
.
Величина ее, как показывают опыты в
трубопроводах круглого сечения, зависит
от рода жидкости, характеризуемого
динамической вязкостью
 ,
и плотностью, а также от диаметра
трубопровода
,
и плотностью, а также от диаметра
трубопровода
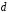 .
.
Многочисленными опытами установлено, что при напорном течении в круглой трубе относительно малым значениям числа Рейнольдса соответствует ламинарный режим, а относительно большим - турбулентный.
Число Рейнольдса, ниже которого наблюдается устойчивое ламинарное течение, получило название нижнего критического, т.е.
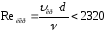 -
ламинарное течение. (3.2)
-
ламинарное течение. (3.2)
При числе Рейнольдса, превышающем верхнее критическое, наблюдается устойчивый турбулентный режим
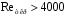 -
турбулентное течение.
-
турбулентное течение.
В узком интервале чисел Рейнольдса между критическим нижним и критическим верхним наблюдается «переходный режим», не имеющий самостоятельного значения и отличающийся крайней неустойчивостью (рис.3.1,б):
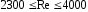 -
переходной режим.
-
переходной режим.
В
этом диапазоне значений чисел
 может существовать как ламинарное, так
и турбулентное течение, но оба они здесь
неустойчивы и легко переходят друг в
друга. Таким образом, для определения
режима движения жидкости в круглом
трубопроводе при напорном движении
достаточно вычислить по формуле (3.1)
число Рейнольдса и сравнить его с
критическим.
может существовать как ламинарное, так
и турбулентное течение, но оба они здесь
неустойчивы и легко переходят друг в
друга. Таким образом, для определения
режима движения жидкости в круглом
трубопроводе при напорном движении
достаточно вычислить по формуле (3.1)
число Рейнольдса и сравнить его с
критическим.
Наличие двух режимов течения можно объяснить тем, что при малых числах Рейнольдса, силы вязкости достаточно велики по сравнению с инерционными силами. Поэтому тормозящее (направляющее) воздействие стенок, осуществляемое через механизм внутреннего трения, распространяется на всю толщу потока. При больших числах Рейнольдса, т.е. при относительно малой роли вязкости, направляющее воздействие стенок может оказаться настолько слабым, что отдельные частицы жидкости под влиянием всякого рода возмущений начнут совершать собственные движения, характерные для турбулентного потока.
Нижнее критическое число Рейнольдса имеет относительно стабильное значение, верхнее же может существенно изменяться под воздействием различных факторов: наличие или отсутствие возмущений на входе, степени шероховатости стенок, наличия или отсутствия вибрации трубы, степени её интенсивности и др.
Знание
режима, движения жидкости необходимо
для правильной оценки потерь напора
при гидравлических расчетах. Потери
напора
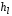 в
зависимости от средней скорости
в
зависимости от средней скорости
 могут
быть представлены в виде графика (рис.
3.2). При ламинарном режиме потери напора
могут
быть представлены в виде графика (рис.
3.2). При ламинарном режиме потери напора
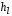 пропорциональны средней скорости
пропорциональны средней скорости
 в первой степени, а при турбулентном -
в степени
в первой степени, а при турбулентном -
в степени
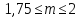 .
С помощью построенного графика определяют
величину критической скорости
.
С помощью построенного графика определяют
величину критической скорости
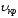 ,
а через нее - и критическое число
Рейнольдса по формуле (3.2).
,
а через нее - и критическое число
Рейнольдса по формуле (3.2).
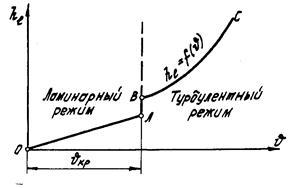
Рисунок 3.2 – Зависимость потерь напора от средней скорости
Описание
установки
(рис 3.3) включает в себя напорный бак 1,
стеклянную прозрачную трубу 2, в которой
изучается движение воды при различных
режимах. На трубе расположены пьезометры
3 для определения потерь напора по длине
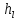 (по разности их показаний). Регулирование
расхода воды, а, следовательно, и средней
скорости ее движения в трубе, осуществляется
краном 4. Для определения расхода воды
во время опытов служат мерный бак 5 и
секундомер 7. Из бачка 6 в поток по
тоненькой трубке подаётся краситель
для визуального определения режима
течения жидкости во время опыта.
Гидравлические потери определяются по
индикатору разницы уровней в пьезометрах
8.
(по разности их показаний). Регулирование
расхода воды, а, следовательно, и средней
скорости ее движения в трубе, осуществляется
краном 4. Для определения расхода воды
во время опытов служат мерный бак 5 и
секундомер 7. Из бачка 6 в поток по
тоненькой трубке подаётся краситель
для визуального определения режима
течения жидкости во время опыта.
Гидравлические потери определяются по
индикатору разницы уровней в пьезометрах
8.
Температура
воды в баке принимается равной 20 0С.
Кинематическая
вязкость воды при
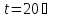 ,
,
 . Внутренний диаметр трубы
. Внутренний диаметр трубы
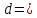
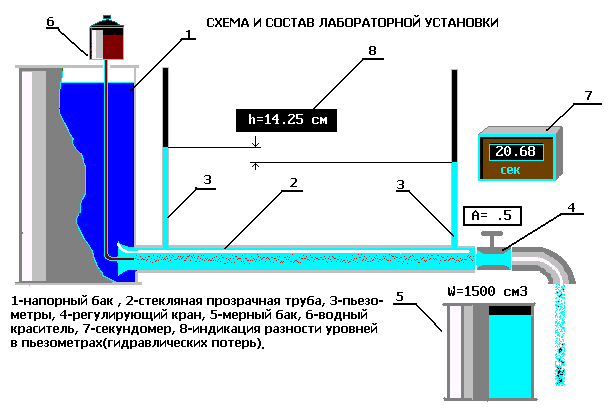
Рисунок 3.3 – Схема экспериментальной установки
Порядок выполнения работы и обработка опытных данных
-
Открыть компьютерную версию лаборатории для имитационного выполнения лабораторных работ при изучении дисциплин «Гидравлика». Включить виртуальную установку для экспериментального исследования режимов движения жидкости.
-
Установить минимальное значение А открытия крана 4 на стеклянной трубе 2. Визуально определить режим течения жидкости.
-
Записать в таблицу 3.1 экспериментальные показания приборов: объёма мерного бака -
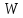 ,
времени наполнения -
,
времени наполнения -
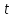 ,
гидравлических потерь -
,
гидравлических потерь -
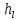 .
. -
Увеличивая расход воды, последовательно провести опыты для восьми - десяти (8 - 10) значений А открытия крана 4.
-
Обработать экспериментальные данные и произвести необходимые вычисления.
-
Построить график зависимости гидравлических потерь от средней скорости течения воды
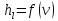 .
По графику определить критическую
скорость
.
По графику определить критическую
скорость
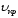 ,
а через неё и значение критического
числа Рейнольдса -
,
а через неё и значение критического
числа Рейнольдса -
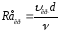 .
. -
Дать заключение по результатам работы.
Таблица 1.3 - Протокол результатов измерений и вычислений
|
№ |
Измеряемых и вычисляемые величины |
Ед. изм. |
Результаты измерений и вычислений |
|||||||
|
Ламинарный режим |
Турбулентный режим |
|||||||||
|
Опыты |
||||||||||
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
Режим течения, визуально |
лам, турб. |
|
|
|
|
|
|
|
|
|
2 |
Объём воды в мерном
сосуде
|
см3 |
|
|
|
|
|
|
|
|
|
3 |
Время
наполнения объёма
|
с |
|
|
|
|
|
|
|
|
|
4 |
Потери
напора по длине
|
см |
|
|
|
|
|
|
|
|
|
5 |
Расход
воды
|
см3/с |
|
|
|
|
|
|
|
|
|
6 |
Внутренний диаметр
стеклянной трубы
|
см |
|
|
|
|
|
|
|
|
|
7 |
Площадь
попереч. сечения трубы
|
см2 |
|
|
|
|
|
|
|
|
|
8 |
Средняя
скорость движения воды
|
см/с |
|
|
|
|
|
|
|
|
|
9 |
Температура воды |
|
20 |
20 |
20 |
20 |
20 |
20 |
20 |
20 |
|
10 |
Кинематический
коэффициент вязкости воды
|
см2/с |
0,01 |
0,01 |
0,01 |
0,01 |
0,01 |
0,01 |
0,01 |
0,01 |
|
11 |
Число Рейнольдса
|
- |
|
|
|
|
|
|
|
|
|
|
Число Рейнольдса
|
- |
|
|
|
|
|
|
|
|
Кинематическая
вязкость воды при
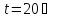 ,
,
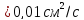 .
.
Контрольные вопросы
-
Назовите режимы движения жидкости и укажите их характерные особенности.
-
Поясните, что такое критерий Рейнольдса, и назовите факторы, от которых он зависит.
-
Поясните, что такое критическое число Рейнольдса?
-
Поясните, каким образом при гидравлических расчётах определяют режим движения жидкости и, с какой целью?
-
Поясните, что такое критическая скорость, от каких факторов она зависит и как её определяют?
-
Напишите и поясните аналитические зависимости потерь напора по длине от средней скорости потока при ламинарном и турбулентном режимах движения жидкости.
-
Изобразите график зависимости потерь напора по длине от средней скорости ( в логарифмических координатах) и дайте пояснения к нему.
Библиографический список
-
Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов (Т.М. Башта, С.С. Руднев, Б.Б. Некрасов и др. - М. : Машиностроение, 1982 . - 423 с.
-
Альтшуль А.Д., Кисилёв П.Г. Гидравлика и аэродинамика (основы механики жидкости) : Учебное пособие для студентов вузов, обучающихся по специальности “Теплогазоснабжение и вентиляция”. - М.: Стройиздат, 1975 . - 327 с.