При одновременном учете влияния давления и температуры

(1.27)

В качестве примера, в котором необходимо учитывать переменность вязкости, рассмотрим случай ламинарного течения жидкости в зазоре между двумя параллельными пластинами под действием избыточного давления при начальной температуре(рис. 8).

Рис.8. Схема ламинарного течения в плоскопараллельном

зазоре при переменной вязкости жидкости

Определим закон изменения давления вдоль зазора, а также расход жидкости через него. Так как при движении жидкости работа сил трения переходит в тепло, то между давлением и температурой жидкости в каждом сечении зазора существует определенная зависимость. Пусть в некотором сечении x от входа избыточное давление равно р и температура t. Тогда, считая, что все тепло, выделяемое в результате внутреннего трения, воспринимается жидкостью и не передается стенкам, можно записать

(1.28)

Обозначая 1/С = k, получим

, (1.29)

где С - удельная теплоемкость в Дж/(кг К);

 - плотность в .

Подставляя этот результат в формулу (1.27) и учитывая, что на выходе давление атмосферное , получаем

. (1.30)

Выделив элементарный участок зазора длиной dx, можем записать по формуле (1.24)

(1.31)

После разделения переменных, интегрирования и несложных преобразований получим следующий закон распределения давления по длине зазора (см. эпюру давлений на рис. 8)

(1.32)

и расход (1.33)

Обозначим , (1.34)

где-расход через зазор, вычисленный в предположении .

Таким образом, окончательно получаем

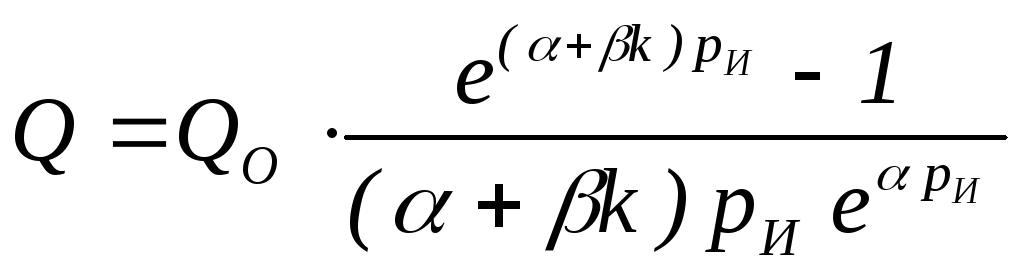. (1.35)

Рассмотрим еще один пример решения данного типа задач.

В рабочей полости, образованной обрабатываемой внутренней цилиндрической поверхностью и торцом установленного с радиальным зазором b обрабатывающего инструмента диаметром D и длиной L (рис.9) поддерживается избыточное давление .

Рис. 9. Гидросхема ЭХО внутренних поверхностей

Определить расход жидкости через кольцевую щель при концентричном расположении обрабатываемой поверхности и инструмента, учитывая зависимость вязкости рабочей жидкости от давления и температуры. При расчете для рабочей жидкости принять:

С = 2,1 - удельная теплоемкость;

; - вязкость рабочей жидкости при давлении;

D = 100 мм; L = 160 мм; b = 0,1 мм;

; - опытные коэффициенты, различные для различных жидкостей;

Выделим бесконечно малый кольцевой элемент жидкости, протекающей в радиальном зазоре между поршнем и цилиндром, и составим уравнение его движения

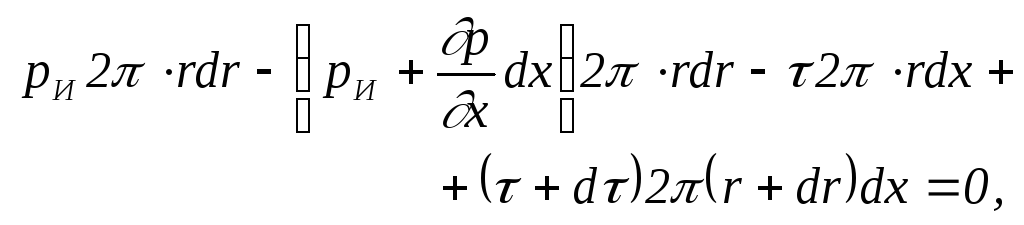(1.36)

где r - расстояние от центральной оси до границы выделенного кольцевого элемента;

dr - толщина кольца;

dx - длина кольцевого элемента;

 - касательное напряжение вязкого трения.

После преобразований в уравнении (1.36) и без учета члена , имеющего более высокий порядок малости по сравнению с остальными членами, получим дифференциальное уравнение в виде

(1.37)

Касательное напряжение  определяется из закона вязкого трения Ньютона, который при изменении вязкости с давлением и температурой можно представить в виде

, (1.38)

где - (1.39)

динамический коэффициент вязкости при давлении p и температуре t;

- динамический коэффициент вязкости при давлении и температуре;

и - опытные коэффициенты, различные для различных жидкостей;

u - локальная скорость течения.

Если принять, что при движении жидкости работа сил трения полностью переходит в тепло, а теплообмен между жидкостью и элементами конструкции отсутствует, то можно записать

, (1.40)

где С - удельная теплоемкость;

 - плотность жидкости;

р - избыточное давление на выходе из зазора.

По условию задачи = 1, т. е. атмосферное, и, соответственно, р = 0. С учетом этого обстоятельства уравнение (1.40) принимает вид

. (1.41)

Решая совместно уравнения (1.39) и (1.41), получим

. (1.42)

При осевом установившемся движении жидкости в кольцевом канале можно считать, что , и. В этом случае функцияв соответствии с уравнением (1.42) также будет не зависящей от координатыr. Разделяя переменные в уравнении (1.37) с учетом уравнения (1.38) и интегрируя его по координате r, будем иметь

(1.43)

Постоянные интегрирования инаходятся из граничных условий, которые требуют, чтобы при иu = 0. При этом уравнение (1.43) принимает вид

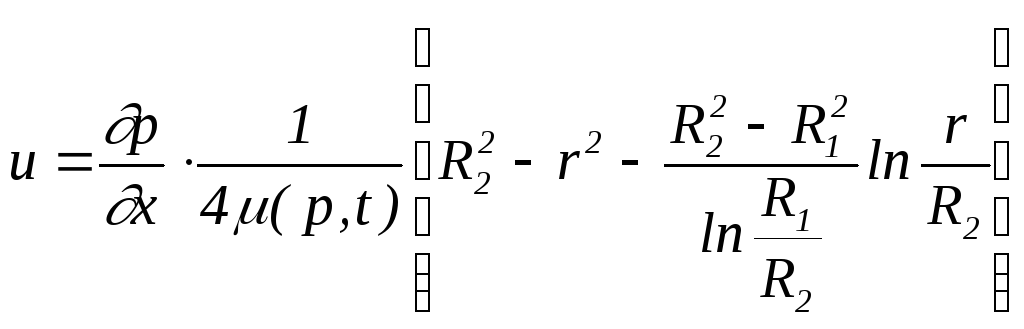. (1.44)

Интегрируя скорость, описываемую уравнением (1.44) по сечению кольцевого зазора, получим выражение для определения расхода жидкости

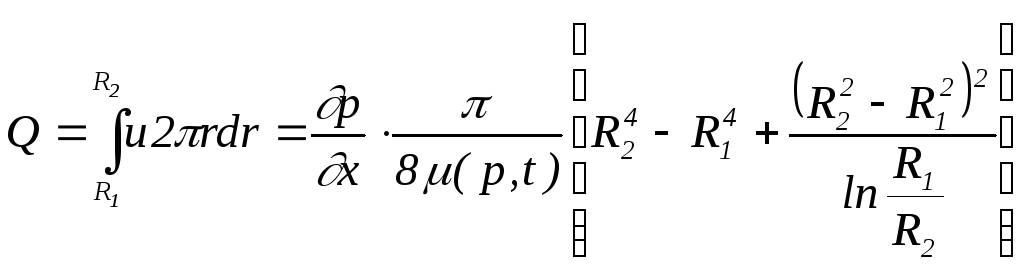. (1.45)

Поскольку давление р является функцией только координаты x, то . Разделяя переменные в уравнении (1.45) и интегрируя его с учетом выражения (1.42), получим уравнение для определения расхода жидкости через кольцевую щель с учетом изменения вязкости жидкости в зависимости от температуры и давления в виде

.

(1.46)

Подставляя численные значения величин в уравнение (1.46), находим

1.2.2. Задача № 3 для самостоятельного решения.

В цилиндр диаметром D (рис. 10) помещен поршень с четырьмя прорезями прямоугольного сечения (s х b).

Рис.10. Гидросхема ЭХО прямоугольных пазов

Пренебрегая потерями напора на входе и выходе, определить расход рабочей жидкости с динамической вязкостью  = 1,5 П по четырем прорезям из левой полости цилиндра, избыточное давление в которой равно Р, в правую, где давление равно атмосферному. Полученный результат сравнить с расходом через кольцевую щель той же площади. Другие исходные данные для решения задачи приведены в приложении 3.

1.2.3. Задача № 4 для самостоятельного решения.

Торцовый зазор между поверхностью диска диаметром и плоскостью составляет величину b (рис. 11).

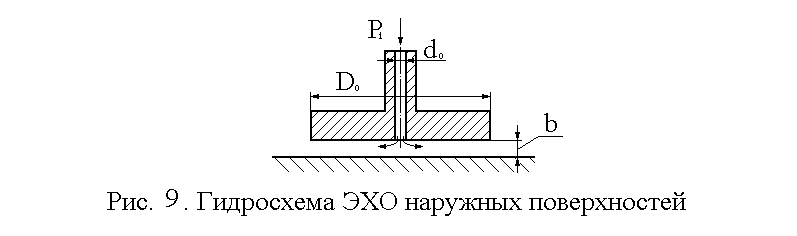
Рис. 11. Гидравлическая схема ЭХО наружных поверхностей

Рабочая жидкость, динамическая вязкость которой равна = 1,5 П, подается к центру зазора по трубке с внутренним диаметром и под избыточным давлением. Требуется:

1) построить эпюру давления по радиусу r диска;

2) вычислить силу давления рабочей жидкости на диск;

3) вычислить расход рабочей жидкости через зазор (скоростными напорами и потерей входа в зазор пренебречь).

Другие исходные данные для решения задачи приведены в приложении 4.