2013.Термодинамика / Свелин200-224-4в-17.10.2012

Многие исследования растворимости, по которым определена низкая растворимость, кажутся сомнительными по этой сущест­венной причине. Томас и Чалмерс [64] экспериментально доказали, что сегрегация растворенного вещества происходит по границам раздела зерен. Например, на рис. 110 показана сегрегация радиоактивного полония в свинце (авторадиография). Потемнение пленки наблюдается в тех местах, где пленка контактирует с участками, обогащенными радиоактивным полонием. Было обнаружено, что количество полония, накапливающегося на границах раздела в свинце, зависит от температуры и степени дезориентации кристаллов на границе раздела. При большей дезориентации по границам раздела имеется больше дислокаций, поэтому можно ожидать, что будет иметь место сегрегация. Это предположение подтверждено.

К изучению сегрегации на границах раздела зерен можно довольно просто подойти с точки зрения статистики. Этот подход может быть также использован и при обсуждении проблемы сегрегации примесей в местах дислокаций. Статистический метод — более общий по сравнению с методом, использовавшимся ранее. Для случая, когда, оба метода идентичны, но они отличаются друг от друга, когдаблизко к 0.

Рассмотрим два типа узлов: находящиеся за пределами дислокационных полей и в поле деформаций границы раздела. В кристалле имеется N узлов первого типа, которые содержат

атомов растворенного вещества; кроме того, в кристалле будет п искаженных узлов, содержащихатомов. Для простоты предположим, что все искаженные узлы эквивалентны и что энтальпия каждого находящегося в них атома равна[44]. Вдали от границы раздела каждый атом примеси будет иметь энтальпиюТаким образом, представляет собой энергию связывания примесей на границе раздела. Число связей, соединяющихатомов с N узлами иатомов с: узлами в этой же самой системе, равно

а энтропия смешения для кристалла равна

Используя приближение Стерлинга, получаем

Свободная энергия кристалла, содержащего . атомов растворителя и атомов растворенного

вещества, равна

Свободная энергия атомов чистого растворителя и атомов чистого растворенного вещества составляет

При, без учета энтропии колебания , свободная энергия смешения равна

(13.17)

Для большинства атомов растворенного вещества наиболее вероятно такое распределение, при которомминимальна. Таким образом, делянаи помня, что , находим причто

(13.18)

Мольная доля растворенного вещества на границе раздела равна

а мольная доля растворенного вещества в массе кристалла

Энергия связывания растворенного вещества с границей раздела равна,где

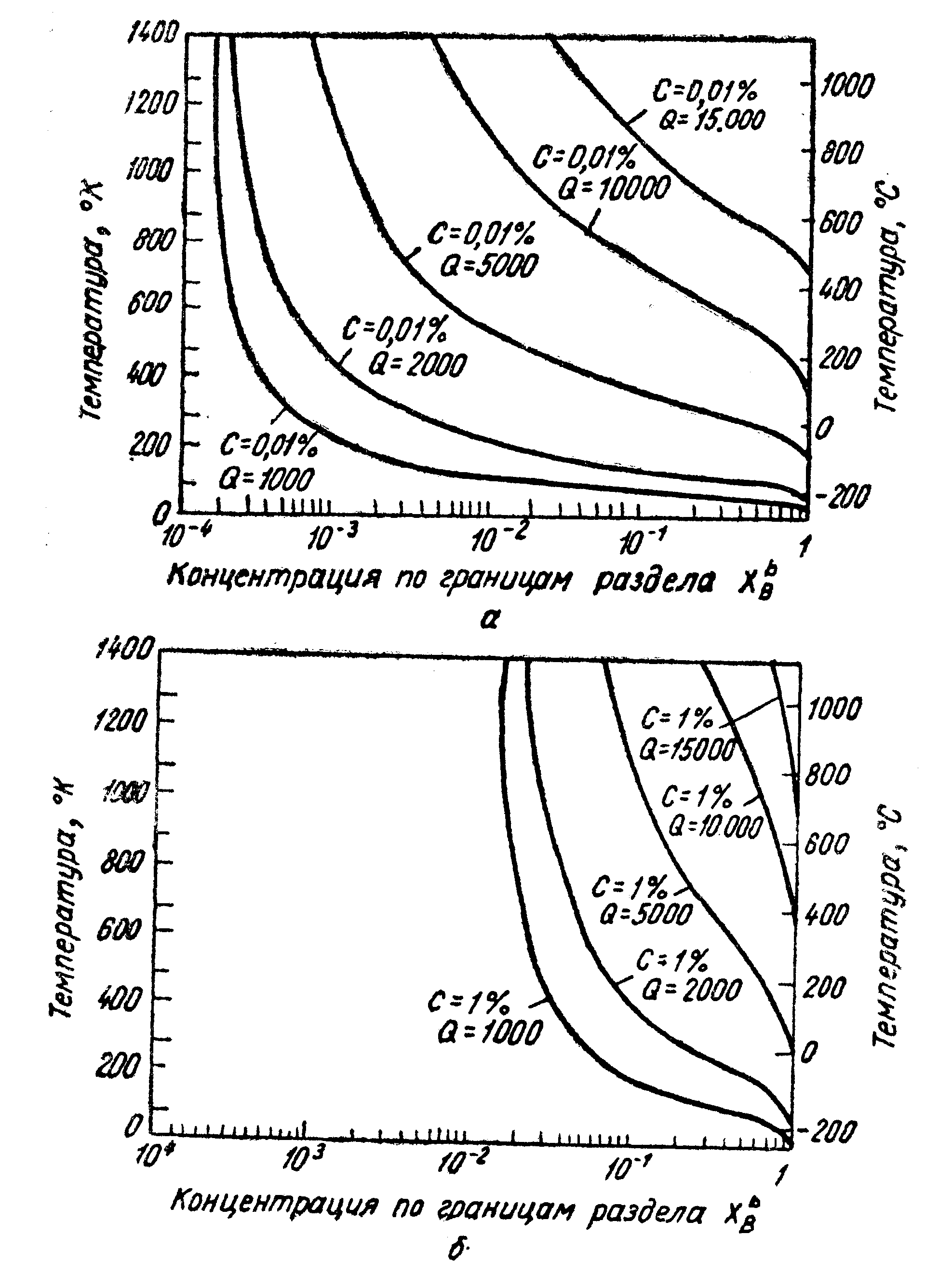
Рис. 112. Зависимость сегрегации от температуры, энергии связывания и концентрации растворенного вещества внутри зерен [44]: — по границам раздела;-—по границам зерен

Отсюда

(13.19)

О

бычно , и, следовательно, мы можем пренебречь по сравнению с единицей в члене в знаменателе; таким образом, (13.20)

Кроме того, если температура довольно высока, то Следовательно, экспоненциалом в делителе можно пренебречь, так как он слишком мал по сравнению с единицей, и тогда

(13.21)

Уравнение (13.21) идентично по форме уравнению (13.16), но оно справедливо только тогда, когда выполняются упомянутые выше условия.

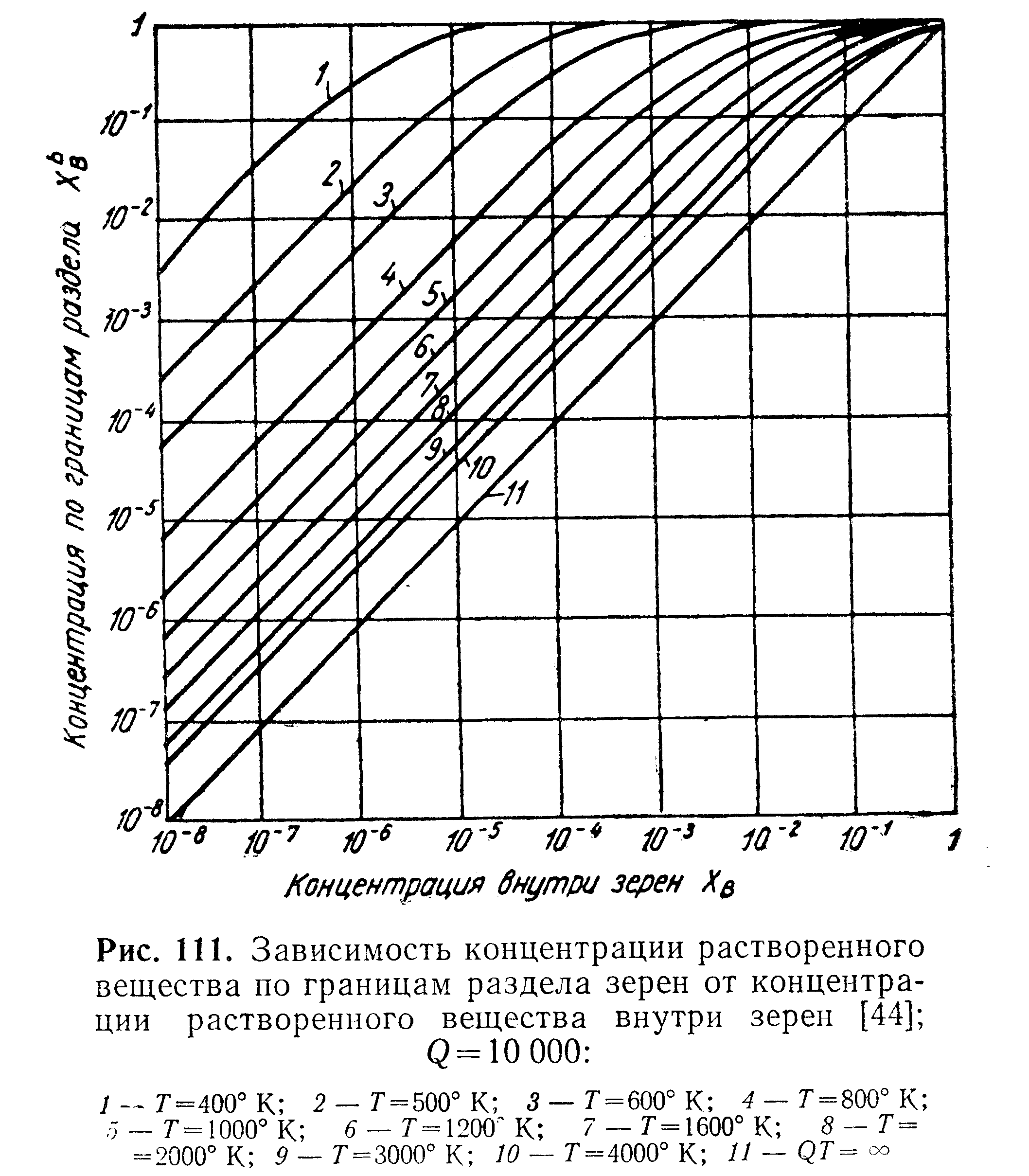
На рис. 111 показана зависимостьотпри разных температурах [вычислено из уравнения (13.20)]. На рисунке видно,

что уравнение (13.21), представляющее собой зависимость

от простого экспоненциального соотношения, справедливо только при высоких концентрациях растворенного в междуузлиях вещества. На рис. 112 показана зависимость степени сегрегации по границам зерен от температуры для различных величин и