
Кинематика. Конспект лекций
.pdfТаким образом, поступательное движение твердого тела можно
изучить по движению какой-либо одной его точки, воспользовавшись
материалом предыдущей лекции.
2.2 Вращение твердого тела вокруг неподвижной оси
Если твердое тело движется так, что две его точки остаются
неподвижными, то такое движение твердого тела называется вращательным движением вокруг неподвижной оси. Такой вид движения в технике встречается чрезвычайно часто: маховик двигателя внутреннего сгорания ротор электродвигателя, патрон шпинделя токарного станка, сверло и т.д.
Ротор, показанный на рисунке 2.5, имеет одну степень свободы.
Наложенные на твердое тело связи позволяют ему совершать только одно движение – вращаться вокруг оси Оz. Положение ротора может быть задано
в форме уравнения вида |
|
(t) . |
(2.1) |
Уравнение (2.1) является законом вращения твердого тела вокруг неподвижной оси.
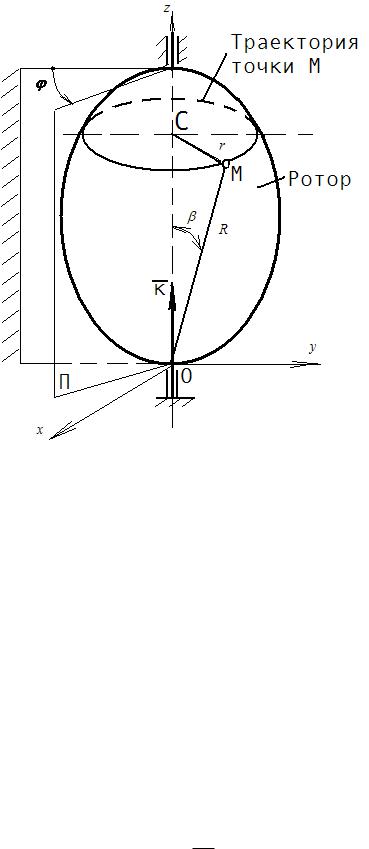
Рисунок 2.5 Вращательным движением тела вокруг неподвижной оси
Угол поворота в системе единиц СИ измеряется в радианах. Иногда в практических расчетах угол выражают числом оборотов N тела. Значения
N и связаны зависимостью
2 N .
Для определения быстроты вращения ротора пользуются понятием
угловой скорости. Пусть в момент времени t положение ротора определяется углом . В момент t1 t t углом поворота 1 , где - приращение угла поворота за промежуток времени t .
Средняя угловая скорость за этот промежуток времени равна
CP t .
Для определения угловой скорости ротора в данный момент времени определим предел средней угловой скорости

lim t 0 |
|
|
d |
|
(2.2) |
t |
|
||||
dt |
. |
Угловая скорость тела в данный момент времени равна первой производной угла поворота по времени. В системе единиц СИ угловая скорость измеряется в радианах в секунду:
рад 1 с 1 .
с с
Во многих случаях угловая скорость ротора меняется. Быстроту изменения угловой скорости характеризуют угловым ускорением в данный момент времени:
СР |
|
; |
lim t 0 |
|
|
d |
|
|
t |
t |
|
||||||
dt |
. |
|||||||
Угловое ускорение тела в данный момент времени равно первой производной по времени от угловой скорости или второй производной от угла поворота. В системе единиц СИ угловое ускорение измеряется в радианах в секунду в квадрате:
|
рад |
|
1 |
с 2 . |
|
|
|
||
|
с2 |
|
с2 |
|
Угловую скорость и угловое ускорение изображают на чертежах |
||||
круговыми стрелками, направляя |
по вращению твердого тела, а в |
|||
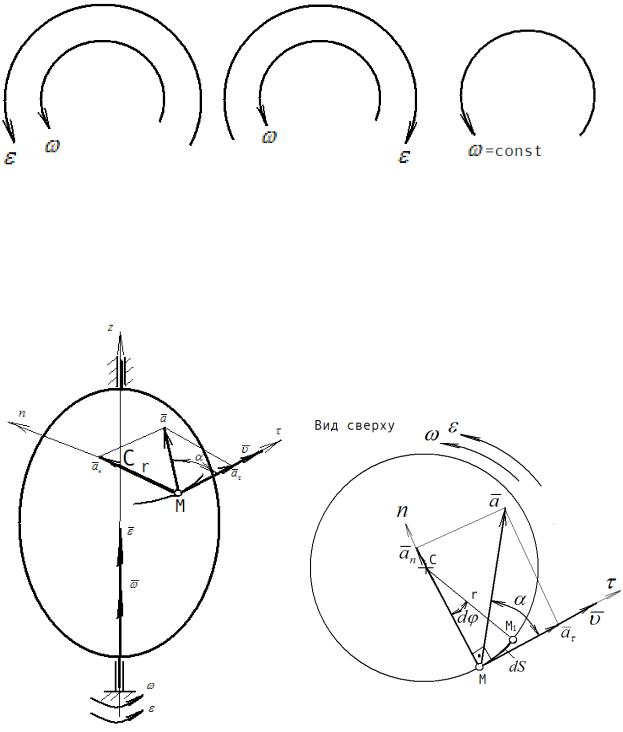
сторону изменения . При этом могут получиться следующие сочетания,
показанные на рисунке 2.6. На рисунке 2.6, а направления и совпадают,
ротор вращается ускоренно. Ротор на рисунке 2.6, б вращается замедленно.
Ротор на рисунке 2.6, в вращается с постоянной угловой скоростью, т.е.
равномерно. В этом случае
0 t .
|
|
|
а |
б |
в |
|
|
|
Рисунок 2.6 Различные случаи вращения твердого тела
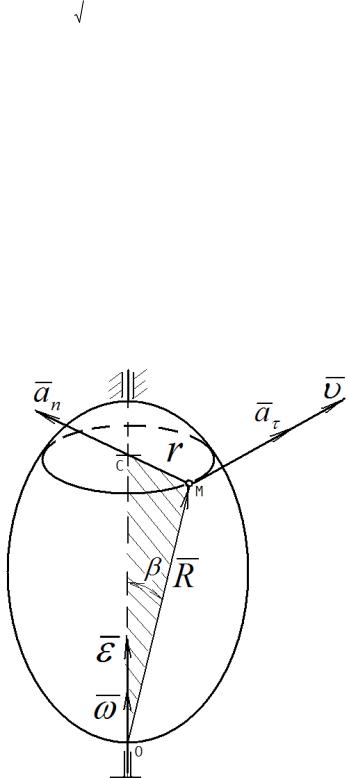
Определим скорость произвольной точки М ротора на рисунке 2.7.
а |
б |
Рисунок 2.7 Определение скорости и ускорения произвольной точки М твердого тела
В соответствии с (1.9) скорость точки М равна dS / dt . По рисунку
2.7, б дуга dS равна dS MM1 d r . Тогда:
|
d |
r r . |
(2.3) |
|
dt |
||||
|
|
|
Воспользуется формулами (1.10-1.12) для определения ускорения
точки:
a a a |
|
|
|
d |
|
|
d |
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
( r)2 |
2 |
|
|
n |
; |
a |
|
|
|
|
|
|
( r) |
|
r |
r |
; a |
n |
|
|
|
|
|
|
r ; |
|||||||||||
|
|
|
dt |
|
dt |
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
a |
|
a |
2 |
a2 |
; |
tg |
|
|
|
|
|
|
|
|
|
(2.4) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
Формулы (2.3, 2.4) для определения скорости и ускорения точки М являются скалярными. Выведем также векторные формулы для определения
этих кинематических характеристик.
Покажем на рисунках 2.7, 2.8 угловую скорость и угловое ускорение,
как вектора |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
, направленные параллельно оси вращения Oz : |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k ; |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
k . |
||||||
Вектора |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
и |
показываем таким образом, чтобы наблюдатель, |
|||||||||||||
смотрящий с их положительных концов, видел соответственно круговые стрелки и , направленными против хода часовой стрелки (рисунки 2.7,
2.8).
Рисунок 2.8 Определение векторов скорости и ускорения точки М
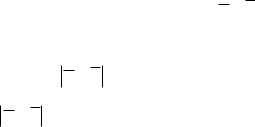
Рассмотрим векторное произведение R . Модуль векторного произведения равен:
R R sin r .
Произведение R направлено перпендикулярно плоскости
т.е. касательно траектории точки М, следовательно, оно является вектором
скорости точки |
|
||||||
|
|
|
|
|
|
(2.5) |
|
|
|
|
|
|
|
|
|
|
R - формула Эйлера. |
||||||
Вектор скорости любой точки тела, вращающегося |
вокруг |
||||||
неподвижной оси, равен векторному произведению вектора угловой скорости тела на радиус-вектор этой точки, проведенный из произвольно выбранной точки, взятой на оси вращения тела.
Определим вектор ускорения точки М.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
d |
|
|
d |
|
|
|
|
|
dR |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
R ; |
a R . |
(2.7) |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
dt |
|
|
|
|
dt |
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
В соответствии с правилом векторного произведения первый |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
R |
в зависимости (2.7) направлен касательно траектории |
||||||||||||||||||||||||||||||||||||||||||||||
слагаемый член |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
точки М, его модуль равен |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
R sin r . |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Следовательно, первый слагаемый в (2.7) является касательной |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
составляющей ускорения |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
R . |
|
|
|
|
|
|
|
|
|
(2.8) |
|||||||||||
|
В соответствии с правилом векторного произведения второй слагаемый |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
член |
|
|
|
направлен к оси вращения Oz , его модуль равен |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 90o 2 r an |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
Следовательно, |
второй слагаемый член в (2.7) является нормальным |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ускорением точки М ротора |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
|
|
|
. |
(2.9) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Примеры решения задач

Задача 2.1 Вал радиуса R = 10 см приводится во вращение гирей,
привешенной к нему на нити (рисунок 1, а). Движение гири выражается
уравнением x 100t 2 , где x - расстояние гири от места схода нити с поверхности вала, выраженное в сантиметрах, t - время в секундах.
Определить угловую скорость и угловое ускорение вала, а также полное ускорение точки М на поверхности вала в момент t .
Решение. Механическая система содержит два твердых тела – гирю 1,
движущуюся поступательно и вал 2, вращающийся вокруг неподвижной оси.
Определим скорость и ускорение гирьки в любой момент времени:
|
|
|
м/с; |
|
2 |
2 |
. |
|
|
1 x 2t |
a1 1 |
м/с |
|||
|
|
|
|
||||
Покажем вектора 1 и a1 на чертеже рисунок 1,б. |
|
||||||
Определим угловую скорость и угловое ускорение вала:
|
1 |
|
2t |
20t |
|
|
2 |
|
|
|
|
рад/с; |
рад/с . |
||||
R |
0,1 |
20 |
||||||
Покажем и на чертеже круговыми стрелками.
Скорость произвольной точки М на поверхности вала равна
R 20t 0,1 2t м/с.
Ускорение точки складывается из двух составляющих
a an a .
Определяем и показываем на чертеже нормальное и касательное
ускорения точки М:
a |
n |
2 |
R (20t)2 |
0,1 40t 2 |
м/с2; |
a R 20 0,1 2 |
м/с2. |
|
|
|
|
|
|
|
Полное ускорение точки М в любой момент времени равно
|
|
|
|
|
|
a a2 |
a2 |
|
(40t 2 )2 22 м/с2. |
||
|
n |
|
|
|
|
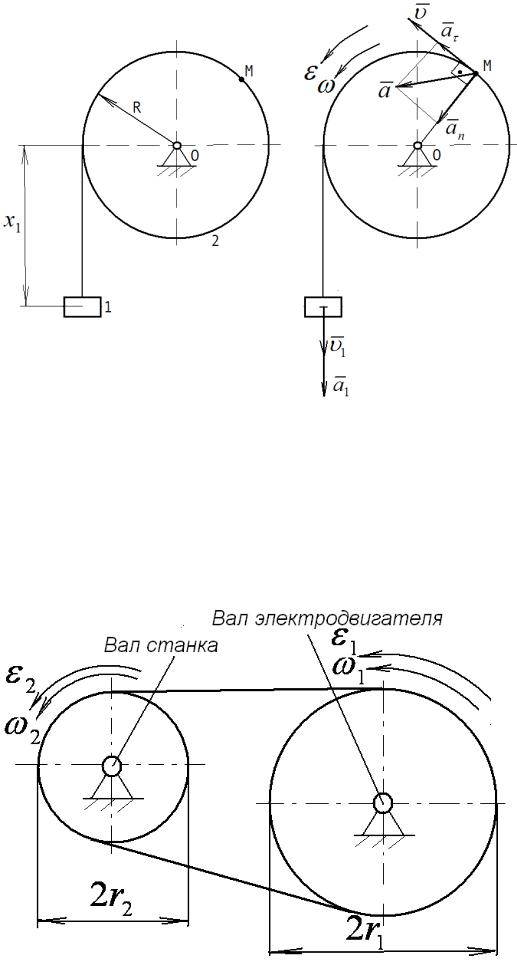
Задача 2.2 Станок со шкивом 2 приводится в движение из состояния покоя бесконечным ремнем от швива 1 электродвигателя (рисунок ).
Радиусы шкивов r1 = 75 см и r2 = 30 см; после пуска в ход электродвигателя его угловое ускорение равно ε1 = 0,4π рад/с2. Пренебрегая скольжением ремня по шкивам, определить через какое время угловая скорость станка будет равна ω2 = 10π рад/с.

|
|
|
Рисунок |
Привод металлорежущего станка |
|||||||||
Решение. Вычислим передаточное отношение ременной передачи. При |
|||||||||||||
отсутствии проскальзывания ремня оно равно |
|
||||||||||||
|
|
|
|
|
i |
|
1 |
|
r2 |
|
|
0,3 |
0,4 . |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
12 |
2 |
|
r1 |
0,75 |
|
|||
|
|
|
|
|
|
|
|
|
|||||
Определим угловое ускорение вала станка |
|||||||||||||
|
|
|
|
2 |
|
1 |
/ i 0,4 / 0,4 рад/с2. |
||||||
|
|
|
|
|
12 |
|
|
|
|
|
|
||
Угловое ускорение равно первой производной по времени от угловой |
|||||||||||||
скорости: |
|
|
|
|
|
|
|
|
|
|
|
||
|
d 2 |
|
|
|
10 |
|
|
|
|
||||
2 |
; |
d 2 2 dt ; |
|
d 2 2 |
dt ; |
10 ; 10 с. |
|||||||
|
|
||||||||||||
|
dt |
|
|
|
0 |
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
ЛЕКЦИЯ 3. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
3.1 Относительное, переносное и абсолютное движение
Сложным (или составным) называется такое движение точки, когда она участвует одновременно в двух или нескольких простых движениях. Так точка М на рисунке 3.1 перемещается по траектории АВ по подвижному
телу. Положение точки М в |
подвижной системе осей |
координат |
|
|
|
xyz определяется радиус-вектором |
R . Положение начала О |
подвижной |
системы отсчета относительно неподвижных осей координат определяется радиусом-вектором rO . Положение точки М относительно неподвижной системы отсчета x1 y1 z1 определяется радиус-вектором r .
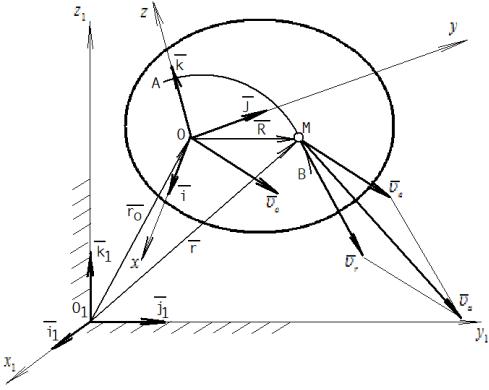
Рисунок 3.1 Сложное (составное) движение точки М
Движение, совершаемое точкой по отношению к подвижной системе осей координат xyz , называется относительным движением. Для обозначения
относительного движения применяется индекс « r ».
Движение подвижной системы осей координат xyz , т.е. всех точек твердого тела по отношению к неподвижной системе x1 y1 z1 называется переносным движением. Для обозначения переносного движения применяется индекс « e ».
Движение точки М относительно неподвижной системы осей
координат называется абсолютным. Для обозначения абсолютного
движения применяется индекс « a ».
Рассмотрим несколько примеров сложного движения точки,
приведенных на рисунке 2.2.
