
- •Билет №1.Числовые множества. Модуль. Элементарные ф-ции. Графики. Преобразование графиков.
- •Алгебраические:
- •Билет №2. Числовые последовательности. Определение предела числовой последовательности.
- •Билет №4. Свойства пределов числовой последовательности .
- •Билет №5. Пределы ф-ций. Свойства пределов ф-ций.
- •Билет №6. Бесконечно малые и бесконечно большие функции. Сравнение бм.
- •Сравнение бесконечно малых
- •Билет №9. Разрывы функций.
- •Точки разрыва первого и второго рода
- •Билет № 12.Понятие производной функции. Свойства производной.
- •Билет № 13 .Геометрический смысл производной.
- •Билет № 14. Уравнение касательной к графику.
- •Билет №15. Связь понятий. Дифференцируемость ф-ции в точке и ее непрерывность.
- •2) Существует ф-ция в каждой точке непрерывная и не в 1ой точке, не имеющая производной.
- •Билет №16.Дифференциал ф-ции. Произв. Суммы, произведения и отношения 2х ф-ций.
- •Правила дифференцирования.
- •Билет №22. Формулы Тейлора и Маклорена.
- •Билет №25. Исследование функции на выпуклость.
- •Билет №27. Предельные величины в экономике.
- •Билет №28. Эластичность спроса.
- •Билет №29. Оптимизационные задачи в экономике.
Билет №22. Формулы Тейлора и Маклорена.
Ряд Тейлора - разложение функции в бесконечную сумму степенных ф-ций.
Говоря нестрого, формула Тейлора показывает поведение функции в окрестности некоторой точки.
-
Пусть функция
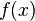 имеет
имеет  производную в
некоторой окрестности
точки
производную в
некоторой окрестности
точки 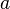 ,
, 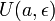
-
Пусть
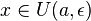
-
Пусть
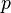 -
произвольное положительное число,
-
произвольное положительное число,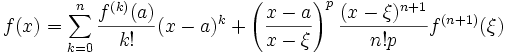
тогда: ![]() точка
точка ![]() при
при ![]() или
или ![]() при
при ![]() :
:
Для
произвольной функции ![]() ,
не являющейся многочленом, формула
Тейлора в окрестности некоторой
точки
,
не являющейся многочленом, формула
Тейлора в окрестности некоторой
точки ![]() принимает
вид:
принимает
вид:![]()
-
остаточный член в асимптотической форме
(в форме Пеано,
в локальной форме)![]()
Остаточный член - разность между заданной ф-цией и ф-цией ее аппроксимирующей. Тем самым оценка остаточного члена является оценкой точности рассматриваемой аппроксимации.
![]()
Полученное
выражение называется формулой
Маклорена для
многочлена ![]() степени
степени ![]() .
.
Можно
разложить многочлен ![]() по
степеням разности
по
степеням разности ![]() ,
где
,
где ![]() -
любое число. В этом случае будем иметь:
-
любое число. В этом случае будем иметь:![]()
Это
выражение называется формулой
Тейлора для
многочлена ![]() в
окрестности точки
в
окрестности точки ![]() .
.
Билет №23. нахождение асимптот графика функции.
Асимптота – прямая, к которой приближаются точки графика функции при бесконечном удалении их от начала координат.
Асимптота может быть вертикальной или наклонной.
Вертикальная А. имеет уравнение x=b , причем f(x)→+∞ (-∞) при x→a (односторонне).
Пусть функция f (x) определена для всех x. Если существуют такие числа k и b, что f(x)-kx-b = 0 при х, то прямая y = kx + b называется наклонной асимптотой графика функции f (x).
k = lim f(x)/x при x→+∞ (x→-∞)
b = lim (f(x)-kx) при x→+∞ (x→-∞)
Пример разных асимптот на разных бесконечностях:
y=
![]()
x→+∞
k = lim
![]() =
lim
=
lim
![]() =
1 b=0
=
1 b=0
x→-∞
k = lim
![]() =
lim
=
lim
![]() =
-1 b=0
=
-1 b=0
Билет №24. Локальный экстремум. Исследование ф-ции на экстремум. Наибольшее и наименьшее значения ф-ции на промежутке.
Экстремум - максимальное или минимальное значение ф-ции на заданном множестве. Точка, в кот. достигается экстремум, называется точкой экстремума. Если достигается минимум - точка min, если максимум - точка max. Также выделают понятие локальный экстремум (минимум/максимум).
Пусть дана
функция ![]() и
и ![]() -
внутренняя точка области определения
-
внутренняя точка области определения ![]() Тогда
Тогда
-
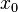 называется
точкой локального максимума функции
называется
точкой локального максимума функции 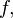 если
существует проколотая окрестность
если
существует проколотая окрестность  такая,
что
такая,
что
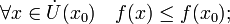
-
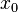 называется
точкой локального минимума функции
называется
точкой локального минимума функции 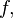 если
существует проколотая окрестность
если
существует проколотая окрестность 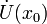 такая,
что
такая,
что
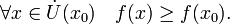
Необходимые условия сущ.:
-
Из леммы Ферма вытекает следующее:
Пусть
точка ![]() является
точкой экстремума функции
является
точкой экстремума функции ![]() ,
определенной в некоторой окрестности
точки
,
определенной в некоторой окрестности
точки ![]() .
.
Тогда либо
производная ![]() не
существует, либо
не
существует, либо ![]() .
.
Достаточные условия существования локальных экстремумов
-
Пусть функция
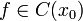 непрерывна
в
непрерывна
в 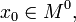 и
существуют конечные или бесконечные
односторонние производные
и
существуют конечные или бесконечные
односторонние производные 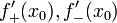 .
Тогда при условии
.
Тогда при условии
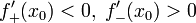
![]() является
точкой строгого локального максимума.
А если
является
точкой строгого локального максимума.
А если
![]()
то ![]() является
точкой строгого локального минимума.
является
точкой строгого локального минимума.
-
Заметим, что при этом функция не дифференцируема в точке
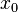 Пусть
функция
Пусть
функция 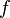 непрерывна
и дважды дифференцируема в точке
непрерывна
и дважды дифференцируема в точке 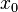 .
Тогда при условии
.
Тогда при условии
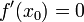 и
и 
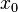 является
точкой локального максимума. А если
является
точкой локального максимума. А если
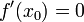 и
и 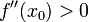
то ![]() является
точкой локального минимума.
является
точкой локального минимума.
-
Пусть функция
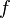 дифференцируема
дифференцируема 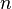 раз
в точке
раз
в точке 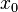 и
и 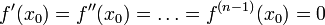 ,
а
,
а 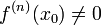 .
. -
Если
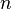 чётно
и
чётно
и 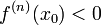 ,
то
,
то 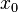 -
точка локального максимума. Если
-
точка локального максимума. Если 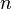 чётно
и
чётно
и 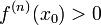 ,
то
,
то 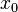 -
точка локального минимума. Если
-
точка локального минимума. Если 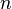 нечётно,
то экстремума нет.
нечётно,
то экстремума нет.
