Билет № 12.Понятие производной функции. Свойства производной.

Производная (функции в точке) определяется как предел отношения приращения ф-ции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Ф-цию, имеющую конечную производную (в точке), называют дифференцируемой (в точке).

Процесс вычисления производной называется дифференцированием. Обратный процесс - нахождение первообразной - интегрирование.

Пусть y=f(x) определена в О(x₀) и пусть x₀+Δx ∈ O(x₀) Δf = f(x₀+Δx) - f(x₀) – приращение функции в точке х₀, соответствующее приращению Δх.

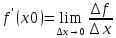Говорят также, что производная - это скорость изменения функции.

Следующие свойства производной служат дополнением к правилам дифференцирования:

• если ф-ция дифференцируема на инте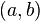рвале , то она непрерывна на интервале 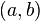. Обратное, вообще говоря, неверно (например, функция 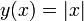 на );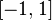

• если ф-ция имеет локальный максимум/минимум при значении аргумента, равном 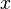, то  (это так называемая лемма Ферма);

• производная данной ф-ции единственна, но у разных ф-ций могут быть одинаковые производные.

• 

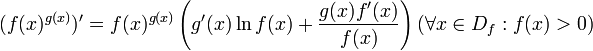
Билет № 13 .Геометрический смысл производной.

С геометрической точки зрения дифференциал – это приращение касательной, отвечающее данному приращению аргумента.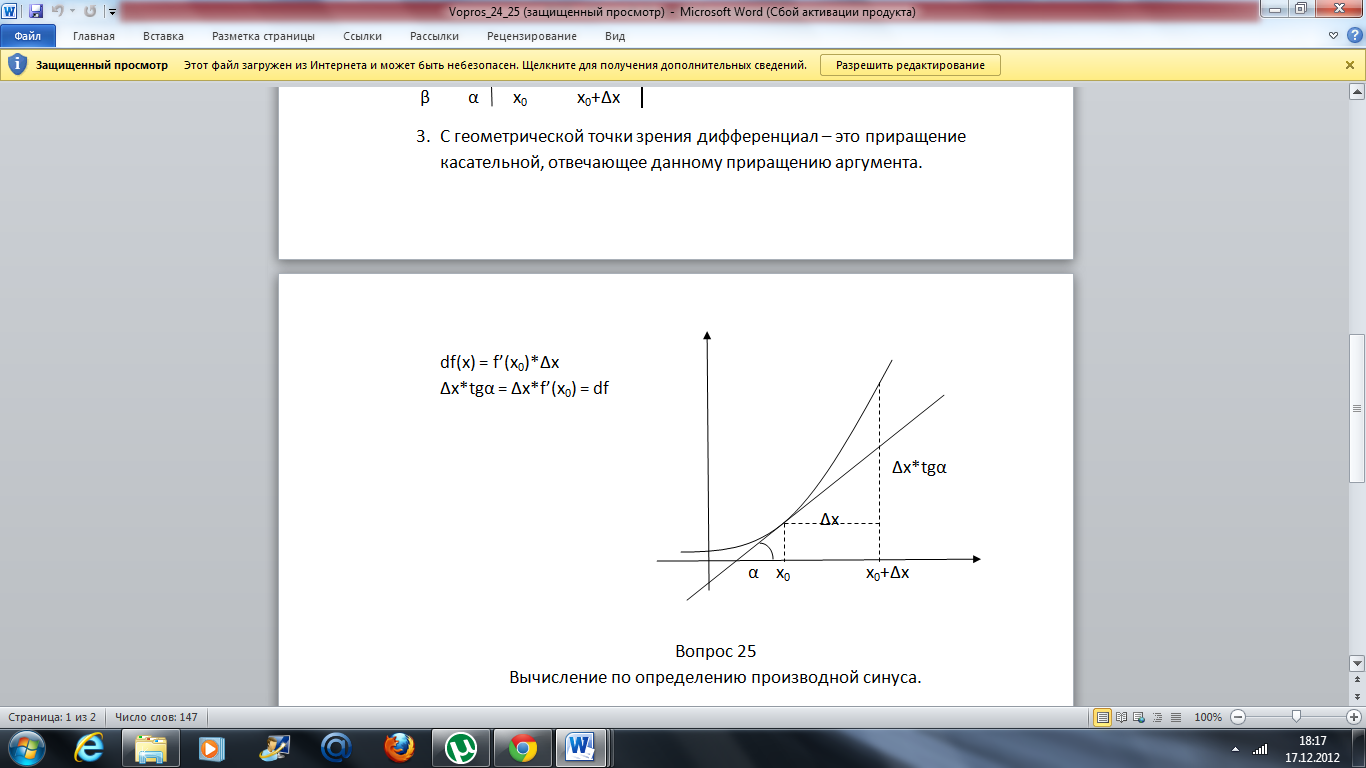

Если функция  имеет конечную производную в точке  то в окрестности  её можно приблизить линейной функцией

Ф-ция  называется касательной к  в точке  Число  является угловым коэффициентом или тангенсом угла наклона касательной прямой.

Скорость изменения функции

Пусть  - закон прямолинейного движения. Тогда  выражает мгновенную скорость движения в момент времени  Вторая производная  выражает мгновенное ускорение в момент времени 

Вообще производная функции  в т.  выражает скорость изменения ф-ции в т. , то есть скорость протекания процесса, описанного зависимостью 

Билет № 14. Уравнение касательной к графику.

Определение: при данном Δх прямая, соединяющая точки (х₀;f(x₀)) и (х₀+Δх;f(x₀+Δx)), называется секущей при данном приращении Δх.

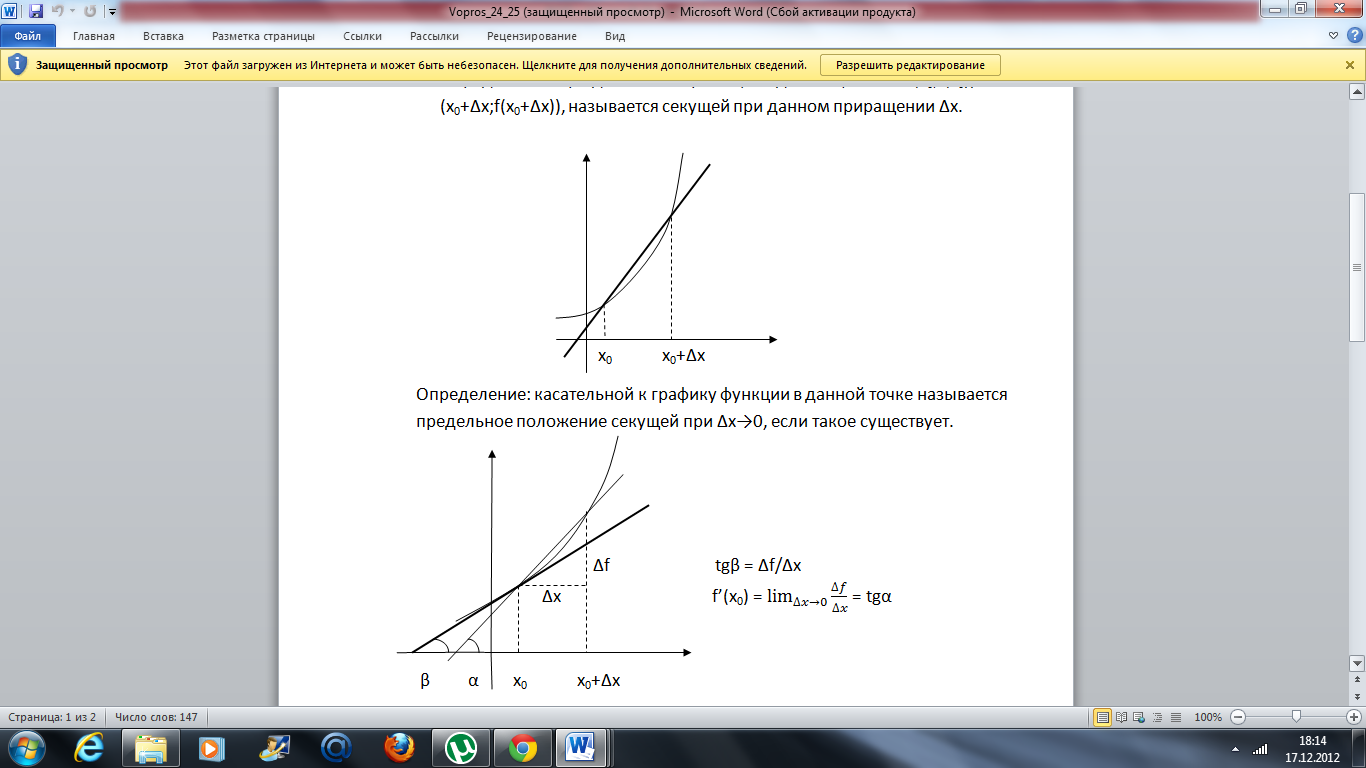
Пусть дана функция f, которая в некоторой точке x₀ имеет конечную производную f (x₀). Тогда прямая, проходящая через точку (x₀; f (x₀)),имеющая угловой коэффициент f ’(x₀), называется касательной.

Касательная прямая - прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.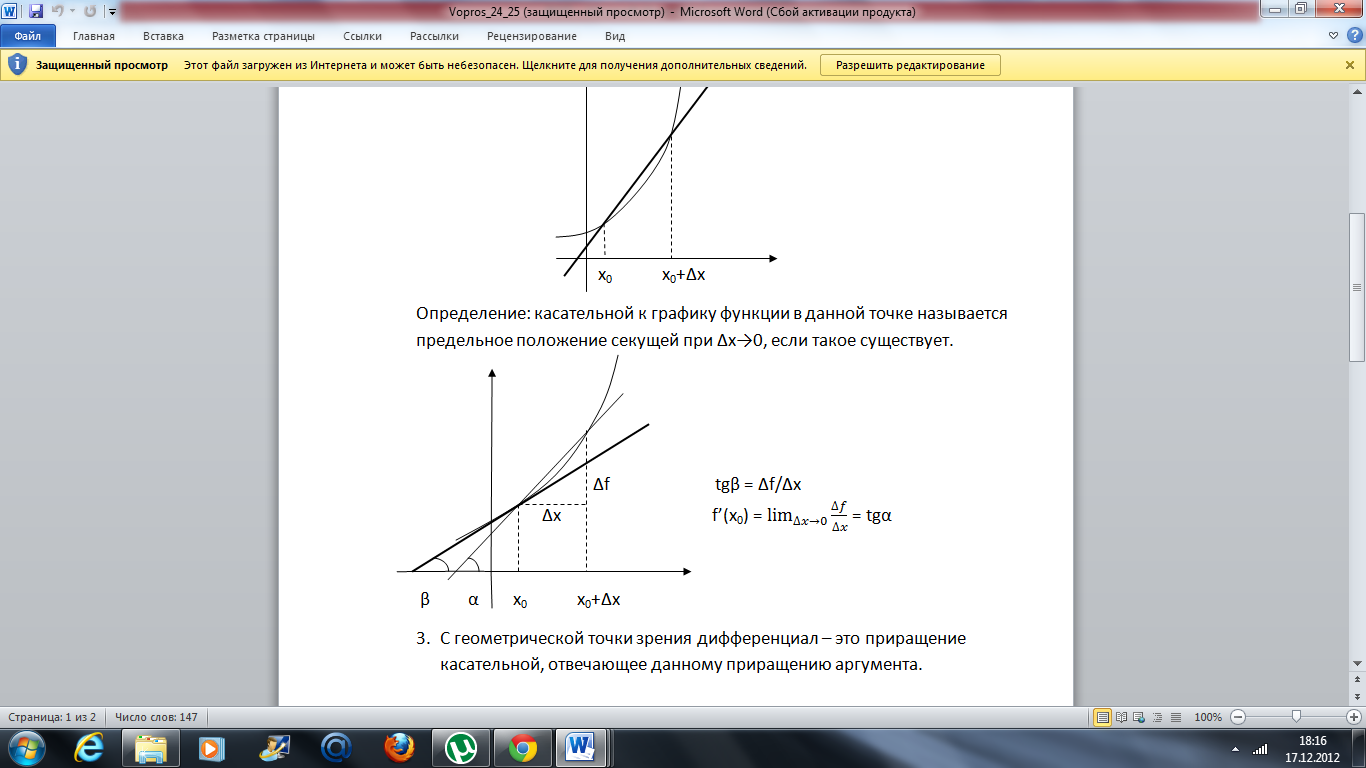

Определение: касательной к графику функции в данной точке называется предельное положение секущей при Δх→0, если такое существует.

 

Билет №15. Связь понятий. Дифференцируемость ф-ции в точке и ее непрерывность.

Теорема: если ф-ция дифференцируема в точке , то она непрерывна данной точке (если ф-ция имеет производную, то она непрерывна).

Непрерывность означает f(x0)=lim f(x) x 0. Это тоже, что f 0.

!!!непрерывная ф-ция не обязана быть дифференцируемой.

Пример: y=|x| непрерывна в т. х=0, но не дифференцируема.

Определение Ф-ция y=f(x) называется дифференцируемой в точке x0, если ее приращение Δy в т. x0 может быть представлено в виде: Δy=A·Δx+α(Δx)·Δx, где A - некоторое число, независящее от Δx, а α(Δx)-- бесконечно малая ф-ция от переменной Δx, т.е. limΔx→0α(Δx)=0.

Теорема. Для того, чтобы ф-ция y=f(x) была дифференцируема в т. x0, необходимо и достаточно, чтобы она в этой точке имела конечную производную. Необходимость. Предположим: ф-ция дифференцируема в точке x0, т.е. Δy=A·Δx+α(Δx)·Δx. Разделив обе части данного равенства на Δx, получим: ΔxΔy=A+α(Δx). Из определения производной ф-ции в точке: y/(x0)=limΔx→0ΔxΔy=limΔx→0(A+α(Δx))=A.

Т.е. получили, что существует конечная производная ф-ции в точке x0 и y/(x0)=A. Достаточность. Пусть существует конечная производная y/(x0)∈R . Покажем дифференцируемость ф-ции. y/(x0)=limΔx→0ΔxΔy.

Если ф-ция f(x) имеет конечный предел b при Δx→0 , то ее можно представить: f(x)=b+α(x) (α(x)→0) . Исходя из этого: ΔxΔy=y/(x0)+α(Δx), где limΔx→0α(Δx)=0, Δy=y/(x0)·Δx+α(Δx)·Δx→ A=y/(x0) . Теорема доказана.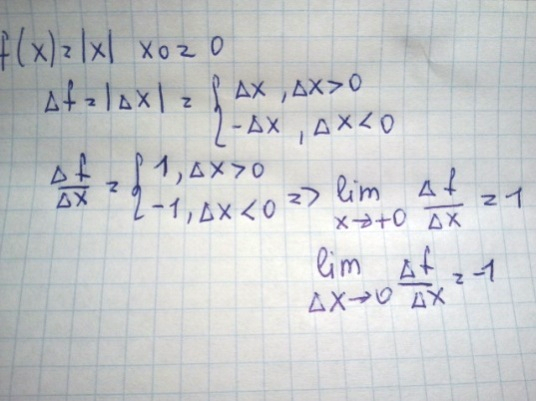

Здесь односторонние приделы не совпадают, значит предел не существует.

Замечание: 1)понятие производной и понятие дифференцируемая вводится также и для ф-ции нескольких переменных. В случае нескольких переменных эти понятия не совпадают.