Билет №9. Разрывы функций.

Понятие устранимого разрыва :

Теорема: предел функции в точке существует тогда и только тогда, когда существуют односторонние пределы.

Lim f(x)= a <-> Lim f(x) =a = Lim f(x) _ X  X 0 + O X X 0 – O

Точка X 0 - точка разрыва,если в ней ф-ция неопределенна или не является непрерывной.

Устранимый разрыв - разрыв, при котором ф-ция определяется так, что она становится непрерывной.

Lim f(x) =a = Lim f(x)

X  X 0 - O X X 0 + O

Если предел ф-ции существует, но он не совпадает со значением ф-ции в данной точке: Lim f(x) ≠f(a) , тогда точка называется точкой устранимого разрыва функции. x  a

Точки разрыва первого и второго рода

Если ф-ция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением ф-ции в данной точке), то для числовых функций возникает 2 возможных варианта, связанных с существованием у числовых ф-ций односторонних пределов:

• если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода. Точки устранимого разрыва являются точками разрыва первого рода;

• если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода.

Билет №10. Непрерывность сложной функции. Использование непрерывности ф-ции для вычисления пределов.

Пусть  и .

Функция  непрерывна в точке , если для любого  существует  такое, что для любого

Функция  непрерывна на множестве , если она непрерывна в каждой точке данного множества.

В этом случае говорят, что функция  класса  и пишут:  или, подробнее, .

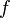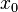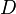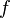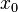• Определение непрерывности фактически повторяет определение предела ф-ции в данной точке. Другими словами, ф-ция  непрерывна в точке , предельной для множества , если  имеет предел в точке , и этот предел совпадает со значением ф-ции .

• Функция непрерывна в точке, если её колебание в данной точке равно нулю.

Билет №11. Функции, непрерывные на отрезке. Их свойства. Примеры.

Ф-цию y = f(x) называют непрерывной на отрезке [a, b], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b, непрерывна соответственно справа и слева.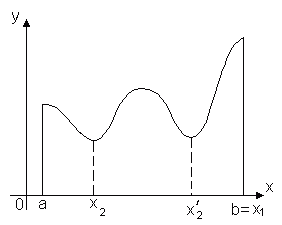

Свойства:(наибольшее и наименьшее значения)

Теорема 1. Функция, непрерывная на отрезке [a, b], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Теорема утверждает, что если ф-ция y = f(x) непрерывна на отрезке [a, b], то найдётся хотя бы 1 точка x₁ (принадл.) [a, b] такая, что значение ф-ции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x₁) ≥ f(x). Аналогично найдётся такая точка x₂, в кот. значение ф-ции будет самым маленьким из всех знач. на отрезке: f(x₁) ≤ f(x).

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что ф-ция f(x) принимает наименьшее значение в двух точках x₂ и x₂'.

Замечание. Утверждение теоремы можно стать неверным, если рассмотреть значение ф-ции на интервале (a, b). Следствие. Если ф-ция f(x) непрерывна на [a, b], то она ограничена на этом отрезке.

Теорема 2 (об ограниченности непрерывной ф-ции). Если ф-ция f(x) непрерывна на отрезке [a,b], то она ограничена на этом отрезке, т.е. существует такое число C>0, что "x О [a,b] выполняется неравенство |f(x)| ≤ C.

Теорема 3. Пусть ф-ция y = f(x) непрерывна на отрезке [a, b] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка [a, b] найдется, по крайней мере, 1 точка x = C, в которой ф-ция обращается в ноль: f(C) = 0, где a < C< b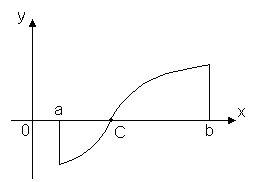

Эта теорема имеет простой геометрический смысл: если точки графика непрерывной функции y = f(x), соответствующие концам отрезка [a, b] лежат по разные стороны от оси Ox, то этот график хотя бы в одной точке отрезка пересекает ось Ox. Разрывные функции этим свойством могут не обладать.

Теорема 4. (теорема о промежуточных значениях). Пусть функция y = f(x) непрерывна на отрезке [a, b] и f(a) = A, f(b) = B. Тогда для любого числа C, заключённого между A и B, найдётся внутри этого отрезка такая точка C [a, b], что f(c) = C.

Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x). Пусть f(a) = A, f(b) = B. Тогда любая прямая y = C, где C – любое число, заключённое между A и B, пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C, при котором f(c) = C.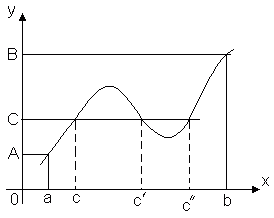

Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями.

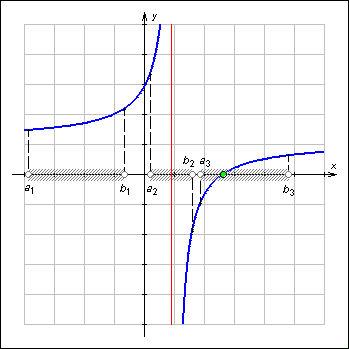
Теорема Коши о нулях непрерывной ф-ции. Только на 1ом из отрезков – [a3; b3] – имеется нуль ф-ции, так как на этом отрезке ф-ция непрерывна и принимает значения разных знаков на концах. Теорема Коши. Если ф-ция f (x) непрерывна на отрезке [a; b] и принимает на его концах значения разных знаков, то на отрезке [a; b] имеется хотя бы 1 нуль ф-ции f. При этом, если ф-ция строго монотонна на этом отрезке, то она принимает значение 0 лишь 1 раз.