Билет №6. Бесконечно малые и бесконечно большие функции. Сравнение бм.

Бесконечно малая - числовая функция, которая стремится к нулю.

Последовательность  называется бесконечно малой, если .

Например, последовательность чисел  — бесконечно малая.

Ф-ция называется бесконечно малой в окрестности точки , если .

Ф-ция называется бесконечно малой на бесконечности, если  либо .

Также бесконечно малой является ф-ция, представляющая собой разность ф-ции и её предела, то есть если , то , .

Бесконечно большая - числовая функция, которая стремится к бесконечности определённого знака. Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (+/-). То есть, напр., ф-ция , неограниченная с обеих сторон, не является бесконечно большой при .

Последовательность  называется бесконечно большой, если .

Ф-ция называется ББ в окрестности точки , если .

Ф-ция называется ББ на бесконечности, если  либо .

Сравнение бесконечно малых

Допустим, у нас есть бесконечно малые при одном и том же  величины  и  (либо, что не важно для определения, бесконечно малые последовательности).

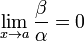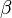• Если , то  — бесконечно малая высшего порядка малости, чем 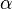. Обозначают 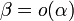 или β≺α.

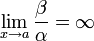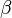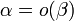• Если , то  — бесконечно малая низшего порядка малости, чем . Соответственно  или α≺β.

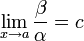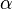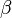• Если  (предел конечен и не равен 0), то  и  являются бесконечно малыми величинами одного порядка малости. Это обозначается как α≍β или как одновременное выполнение отношени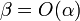й  и .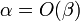

• Если 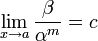 (предел конечен и не равен 0), то бесконечно малая величина  имеет 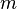-й порядок малости относительно бесконечно малой .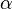

Для вычисления подобных пределов удобно использовать правило Лопиталя.

Билет №7. 2 замечательных предела.

Замечательные пределы - термин, использующийся в математическом аналие для обозначения известных математических тождеств со взятием предела.

Первый замечательный предел:

Доказательство

Рассмотрим односторонние пределы  и  и докажем, что они равны 1.

Пусть . Отложим этот угол на единичной окружности ().

K - точка пересечения луча с окружностью, а точка L - с касательной к единичной окружности в точке (1;0). Точка H - проекция точки K на OX.

Очевидно, что  (1)

(где  — площадь сектора )

(из : )

Подставляя в (1), получим:

Так как при :

Умножаем на :

Перейдём к пределу:

Найдём левый односторонний предел:

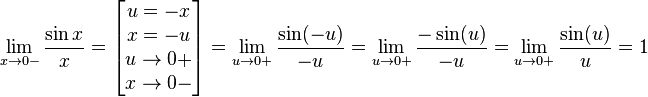
Правый и левый 1-сторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

Второй замечательный предел:

Доказательство для натуральных значений x

Зная, что второй замечательный предел верен для натуральных значений x, докажем 2ой замечательный предел для вещественных x, то есть докажем, что . Рассмотрим 2 случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где  — это целая часть x.

Отсюда следует: , поэтому.

Если , то . Поэтому, согласно пределу , имеем:.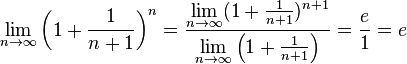

По признаку (о пределе промежуточной функции) существования пределов .

2. Пусть . Сделаем подстановку , тогда.

Из 2х этих случаев вытекает, что  для вещественного x.

Следствия

 для , 

Билет №8. Понятие непрерывной функции.

Непрерывная функция - ф-ция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.

ε-δ определение Пусть и .

Функция непрерывна в точке Xo, если для любого существует такое,

что для любого Функция непрерывна на множестве , если она непрерывна в каждой точке данного множества. Другими словами, функция непрерывна в точке , предельной для множества , если имеет предел в точке , и этот предел совпадает со значением функции . Функция непрерывна в точке, если её колебание в данной точке равно нулю.

Все элементарные функции непрерывны на своей области определения.