Основные свойства точечных оценок

 

Для того чтобы оценка имела практическую ценность, она должна обладать следующимисвойствами. ·     1. Оценка параметра q называетсянесмещенной, если ее математическое ожидание равно оцениваемому параметру q , т.е. М = q .(22.1) Если равенство (22.1) не выполняется, то оценкаможет либо завышать значение q (М > q ), либо занижать его (М < q ) . Естественно в качестве приближенного неизвестного параметра брать несмещенные оценки для того, чтобы не делать систематической ошибки в сторону завышения или занижения. ·     2. Оценкапараметра q называетсясостоятельной , если она подчиняется закону больших чисел, т.е. сходится по вероятности к оцениваемому параметру при неограниченном возрастании числа опытов (наблюдений ) и, следовательно, выполняется следующее равенство: ,(22.2) где e > 0 сколько угодно малое число. Для выполнения (22.2) достаточно, чтобы дисперсия оценки стремилась к нулю при, т.е.(22.3) и кроме того, чтобы оценка была несмещенной. От формулы (22.3) легко перейти к (22.2) , если воспользоваться неравенством Чебышева. Итак, состоятельность оценки означает, что при достаточно большом количестве опытов и со сколько угодно большой достоверностью отклонение оценки от истинного значения параметра меньше любой наперед заданной величины. Этим оправдано увеличение объема выборки. Так как- случайная величина, значение которой изменяется от выборки к выборке, то меру ее рассеивания около математического ожидания q будем характеризовать дисперсией D . Пусть и- две несмещенные оценки параметра q, т.е. M = q и M = q , соответственно D и D и, если D < D , то в качестве оценки принимают . ·     3. Несмещенная оценка, которая имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра q, вычисленных по выборкам одного и того же объема , называется эффективной оценкой.  На практике при оценке параметров не всегда удается удовлетворить одновременно требованиям 1, 2, 3. Однако выбору оценки всегда должно предшествовать ее критическое рассмотрение со всех точек зрения. При выборке практических методов обработки опытных данных необходимо руководствоваться сформулированными свойствами оценок.

Точечная оценка математического ожидания

Задана случайная величина Х:х₁, х₂, …, х_n, так какМ(Х) не найти, то для математического ожидания случайной величиныХ естественно предложить среднее арифметическое

(1.3)

её наблюденных значений.

1. По методу произведений 

,,

так как

.

Это и означает, что оценка несмещенная.

2. Если исследуемая случайная величина Химеет конечную дисперсию, то эта оценка будет состоятельной, так как

.

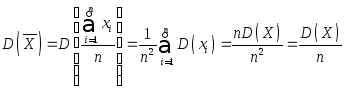Если исследуемая величина имеет нормальный закон распределения, то можно показать, что предложенная оценка эффективна, т. е. оценки для математического ожидания с меньшей дисперсией не существует для нормально распределенных величин

5. Понятие оценки числовой характеристики или параметра распределения. Свойства точечных оценок. Выборочная оценка дисперсии, ее свойства.

Оценивание параметров распределения осуществляется в два этапа. На первом этапе, на основании выборки х1, х2, ... , ,хn ,строится статистика

,

значение которой при данной выборке х1, х2, ... , ,хn принимают за приближенное значение оцениваемого параметра а :

а.

Так как параметр генеральной совокупности оценивается числом, которое на числовой оси изображается точкой, то оценку называют точечной.

Для того чтобы оценка имела практическую ценность она должна обладать следующими свойствами.

1. Несмещенность оценки. Оценка называется несмещенной, если ее математическое ожидание равно оцениваемому параметру генеральной совокупности:

В противном случае оценка называется смещенной и допускает систематическую ошибку.

2. Состоятельность оценки. Оценка называется состоятельной, если она по вероятности с увеличением объема выборки п стремится к параметру генеральной совокупности:

Это условие будет выполняться, если

и оценка является несмещенной. Доказательство этого основано на неравенстве Чебышева.

3. Эффективность оценки. Если составлять множество несмещенных и состоятельных оценок, то эти оценки будут иметь разные дисперсии. Ясно, что, чем меньше будет дисперсия, тем меньше будет вероятность грубой ошибки при определении приближенного параметра генеральной совокупности. Поэтому нужно выбрать такую оценку, у которой дисперсия была бы минимальной:

Такая оценка называется эффективной.

Выборочная дисперсия характеризует разброс (рассеивание) значений вариант хi от выборочного среднего значения х_в и измеряется в квадратных единицах измерения признака Х

Св-ва:Выборочные дисперсии Dв и S² являются состоятельными

оценками для генеральной дисперсии

5. Использование метода моментов для получения точечной оценки параметров непрерывного равномерного распределения

Метод моментов оценивания параметров распределения генеральной совокупности состоит в том, на основании выборки х1, х2, ..., хn вычисляются выборочные моменты (начальные или центральные). Полученные значения приравниваются соответствующим теоретическим моментам. Количество моментов должно ровняться числу оцениваемых параметров. Затем решают полученную систему уравнений относительно этих параметров.

По выборке х1, х2, ... , хп методом моментов найти точечные оценки параметров а1, а2 равномерного распределения на интервале [а1, а2]:

Решение. Используя выборку х1, х2, ... , хп, находим выборочные первый начальный и второй центральные моменты:

,,() (8.2)

Для равномерного распределения имеем теоретические моменты

, .

Прировняем теоретические моменты выборочным и получаем систему двух уравнений с двумя неизвестными для нахождения оценок параметров а1, а2:

Решая эту систему, получаем в окончательном виде

, ,

где величины , определены соотношениями (2)

5. Использование метода моментов для получения точечной оценки параметров нормального распределения.

По выборке х1, х2, ... , хп методом моментов найти точечные оценки параметров mx и нормального распределения:

.

Решение. Так как первый начальный момент нормального распределения равен параметру тх., а второй центральный момент равен параметру ,

то

, .

5. Использование метода моментов для получения нахождения оценки параметра показательного распределения.

Пример. Пусть Х – непрерывная случайная величина подчинена показательному (экспоненциальному) закону, плотность распределения которого зависит от одного неизвестного параметра :

, х0.

Используя полученные экспериментальные данные х1, х2, ... , хn, получить оценку параметра .

Решение. На основании выборки х1, х2, ... , хn находим первый выборочный момент и приравниваем его первому моменту случайной величины Х, подчиненной показательному закону:

= =.

Отсюда получаем оценку параметра :

.▄

Статистика

9-12

9. Использование метода моментов для получения параметров биномиального распределения и геометрического распределения

Метод моментов основан на приравнивании моментов (центральных, начальных) СВ X к их выборочным оценкам. При этом число составляемых уравнений равно числу неизвестных параметров.

Пример.Пусть Х ~ R(a, b), где a и b - неизвестные параметры. Нужно найти точечные оценки A и B параметров a и b соответственно.

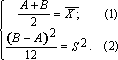
Согласно этому методу нужно вычислить два момента (начальный 1-го порядка и центральный 2-го порядка) СВ X: m_X= (a+b)/2 и D_X= (b-a)²/12 и составить два уравнения (1) и (2), приравнивая моменты (A+B)/2 и (B-A)²/12 к их соответствующим выборочным значениям

и . Следовательно:

10. Основные распределения, используемые в математической статистике:

распределение хи- квадрат. Примеры использования распределения

Нормальное распределение играет исключительно важную роль в математической статистике. Такое распределение наиболее часто встречается на практике. Главная особенность, выделяющая нормальное распределение среди других распределений, состоит в том, что оно является предельным, к которому приближаются остальные распределения при весьма часто встречающихся типичных условиях.

Распределение случайной величины называетсянормальным, если это распределение характеризуется плотностью следующего вида

где математическое ожидание, асреднеквадратическое отклонение(дисперсия). Таким образом, мы видим, что нормальное распределение описывается двумя параметрамии.

Замечание 1. Общим называют нормальное распределение с произвольными параметрами и.Замечание 1*. Нормированной называют нормальное распределение с параметрами иЗамечание 2. Генеральная совокупность называется нормальной, если она распределена нормально.

Распределение основных статистик, которые вычисляются по выборке из нормально распределенной генеральной совокупности, связаны с распределением “хи-квадрат” и Стьюдента.

Распределением сстепенями свободы называется распределение случайной величины, равной сумме квадратовнезависимых нормально распределенных по законуслучайных величин, то есть величины

Плотность этого распределения

где – гамма функция; в частности,

Отсюда видно, что распределение “хи квадрат” определяется одним параметром – числом степеней свободы .

Замечание 3. С увеличением числа степеней свободы распределение медленно приближается к нормальному.

Распределением Стьюдента с степенями свободы называется распределение случайной величины, равной отношению двух независимых случайных величини, то есть

,

где имеет нормальное распределение.

Замечание 4. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному распределению.