Глава 3. РЯДЫ ФУРЬЕ

si n (n m)

si n (n m)

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Политехнический Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

up_2.pdf

Скачиваний:

Добавлен:

29.05.2015

Размер:

1.8 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

		cn
5. Дан степенной ряд cn x 3n , и известно, что l i m		cn		3 . Можно
5. Дан степенной ряд cn x 3n , и известно, что l i m		c		3 . Можно
n 1	n	c	1
n 1		n	1

ли утверждать, что интервалом сходимости этого ряда будет интервал

( 3, 3) ?

		cn 1
6. Дан степенной ряд cn x 4n , и известно, что l i m		cn 1	4 . Найдите
6. Дан степенной ряд cn x 4n , и известно, что l i m		c	4 . Найдите
n 1	n	c
n 1		n

интервал сходимости этого ряда.

7. Оцените погрешность приближённого равенства si n 0, 1 0, 1 .

8. В каких случаях остаточный член Rn (x) формулы Тейлора и остаток ряда Тейлора для одной и той же функции совпадают?


9.	Следует ли	из	сходимости ряда		cn x n	сходимость ряда
					n 1

ncn x n 1 ?
n 1

10. Дан ряд cn x n			и R – его радиус сходимости. Верна ли формула
	n 1
	R			R
	S(x)dx cn			x n dx , где S(x) cn x n .
	0	n 1		0	n 1

11.	Степенной ряд cn x n сходится в точке x b условно. Можно
		n 1
ли утверждать, что радиус сходимости этого ряда равен R b?
12. Не дифференцируя, найдите значение					y(I X ) (0)	девятой производ-
ной в точке x 0		функции y e 2x .
Глава 3. РЯДЫ ФУРЬЕ
§1. Основные понятия
	Рассмотрим последовательность функций
	1 (x) , 2 (x) ,…, n (x) ,…,					(3.1)

непрерывных на отрезке [a; b] , среди которых нет функций, тождественно равных нулю.

Определение 3.1.1. Последовательность функций (3.1) называ-

ется нормированной на отрезке [a; b] , если

( n (x))2 dx 1 для всех n .

Определение 3.1.2. Последовательность функций (3.1) называ-

ется ортогональной на отрезке [a; b] , если

b
n (x) m (x)dx 0	при n m .
a

Определение 3.1.3. Последовательность функций (3.1) называется ортонормальной на отрезке [a; b] , если она является нормированной и ортогональной, т.е.

b				1, если n m,
	(x)		(x)dx	1, если n m,
	n	m		0, если n m.
	n	m
a
Переход от произвольной системы функций 1 (x) ,					2 (x) ,…,

n (x) ,…, заданной на некотором отрезке, к нормированной на этом отрезке системе называется её нормировкой. Для того чтобы его осу-

ществить,

достаточно

для

каждой

функции

из

последовательности

(3.1) вычислить интеграл

( n (x))2 dx n

разделить каждую

функцию n (x)

на число

n . При этом мы действительно получим

нормированные функции

(x )

, n

1, 2,

, так как

(x)

1 b

(

(x))2 dx

1 .

Переход от произвольной системы функций 1 (x) , 2 (x) ,…,n (x) ,…, заданной на некотором отрезке, к ортогональной на этом же

отрезке системе называется её ортогонализацией. Этот процесс более сложен, чем нормировка и даже не всегда возможен.

Рассмотрим ортогональную на отрезке [a; b] последовательность функций (3.1). Рядом по ортогональной системе (3.1) функций

называется ряд вида cn n (x) , где числа cn ( n 1, 2, ) – коэффи-

n 1

циенты ряда.

Пусть функция f (x) является суммой равномерно сходящегося на отрезке [a; b] ряда по ортогональной системе (3.1):

f (x) c1 1 (x) c2 2 (x) cn n (x) (3.2)

Найдём коэффициенты этого ряда. Функции 1 (x) , 2 (x) ,…,n (x) ,… непрерывны на отрезке [a; b] . Поэтому функция f (x) , как сумма равномерно сходящегося на отрезке [a; b] ряда непрерывных функций, является на этом отрезке непрерывной функцией.

Умножим обе части равенства (3.2) на функцию n (x) . В результате получится ряд, равномерно сходящийся на отрезке [a; b] к функции f (x) n (x) . Проинтегрируем новый ряд почленно в пределах от a до b и получим

b b b

f (x) n (x)dx c1 1 (x) n (x)dx c2 2 (x ) n (x )dx

a a a b

cn ( n (x))2 dx

В силу ортогональности системы функций (3.1) все интегралы в

правой части равенства, кроме интеграла ( n (x))2 dx , равны нулю.

			a
Таким образом, получаем соотношение
b			b
f (x) n (x)dx cn ( n (x))2 dx ,
a			a
из которого следует формула для коэффициентов ряда
	b
	f (x ) n (x )dx
c	a		, n 1, 2,	(3.3)
c	b		, n 1, 2,	(3.3)
n	b
	( n (x))2 dx
	a
Ряд (3.2)		называется рядом Фурье функции f (x)		по ортого-

нальной системе функций (3.1). Числа cn , определяемые по формулам (3.3), называются коэффициентами Фурье функции f (x) по системе

(3.1).

Таким образом, для произвольной функции f (x) можно записать ряд Фурье по ортогональной системе

f (x) cn n (x) .

n 1

Если записанный ряд сходится к функции f (x) в каждой точке её непрерывности, принадлежащей отрезку [a; b] , то знак соответствия « » заменяется знаком равенства « = »:

f (x) cn n (x) , x [a, b] .

Вэтом случае говорят, что функция f (x) на отрезке [a; b] раз-

лагается в ряд Фурье по ортогональной системе.

§2. Тригонометрические ряды Фурье

Рассмотрим тригонометрическую систему функций:

1,	cos	x	, si n	x	, cos	2 x	, si n	2 x	,…
		l		l		l		l

Покажем, что эта система функций является ортогональной на отрезке [ l; l] . Для этого вычислим интегралы

n x

m x

n x

m x

cos

dx ,

si n

dx ,

n x

m x

n x

cos

si n

dx ,

1 si n

dx , 1 cos

dx .

n x

m x

(n m) x

∙ cos

cos

1 l 1

si n

(n m) x

si n

(n m) x

n m

si n (n m)

n m

si n (n m)

0 .

n m

n x

m x

(n m) x

∙ si n

si n

cos

1 l 1

si n

(n m) x

si n

(n m) x

n m

si n (n m)

si n (n m) 0 .

n x

m x

(n m) x

(m n) x

∙ cos

si n

cos

(n m) x

cos

(m n) x

n m

m n

cos (n

cos (m n)

n m

m n

cos (n m)

cos (m n) 0 .

m n

n x

∙ 1 si n

(cos(n ) cos( n )) 0 .

cos

n x

∙ 1 cos

si n

(si n(n ) si n( n )) 0 .

При вычислении интегралов мы учли свойства тригонометриче-

ских функций: чётность косинуса cos( ) cos ,

нечётность синуса

si n( ) si n , а также si n k 0 , k .

Таким образом, тригонометрическая система функций является ортогональной на отрезке [ l; l] . Нормированной эта система функций не является, так как

2 n x

2n x

cos

dx si n

cos

1		l		2n x	l

	x		si n			l ,
2		2n		l
					l

12 dx 2l .

Нормировка системы тригонометрических функций на отрезке

[ l; l] состоит в делении 1 на

и каждой из остальных функций на

l . В результате получим ортонормальную на отрезке

[ l; l] триго-

нометрическую систему функций:

cos x ,

si n

cos

2 x

si n

2 x

,…

Ряд Фурье по этой системе функций на

отрезке [ l; l] для

функции f (x)

имеет вид:

n x

f (x)

cos

bn si n

(3.4)

n 1

где коэффициенты Фурье a0 , an ,

bn определяются по формулам (3.3)

и для указанной системы функций имеют вид:

f (x)dx ,

f (x) cos

n x

dx , n 1, 2,

(3.5)

f (x) si n

n x

, n 1, 2,

Ряд (3.4) называется тригонометрическим рядом Фурье, чтобы отличать его от рядов Фурье, получающихся при разложении по другим системам функций. Однако тригонометрические ряды Фурье применяются в теории и практике так часто, что обычно их называют «просто» рядами Фурье.

Отметим, что формула (3.4) носит пока формальный характер, поскольку ещё необходимо получить ответы на следующие вопросы: будет ли сумма ряда Фурье для функции f (x) существовать, и будет

ли она равна самой функции f (x) , может ли ряд Фурье функции f (x) не сходиться вовсе или сходиться, но не к функции f (x) , а к некоторой другой функции?

С подобными вопросами нам уже приходилось сталкиваться при разложении функций в степенные ряды.

Ниже выясним условия, при которых ряд Фурье функции f (x) сходится к этой функции.

§3. Теорема Дирихле

Теорема 3.3.1 (Дирихле). Пусть функция f (x) на отрезке

[ l, l] :

1)непрерывна или имеет конечное число точек разрыва I рода;

2)монотонна или имеет конечное число точек экстремума.

Тогда тригонометрический ряд Фурье для функции f (x) сходится во всех точках отрезка [ l, l] . Его суммой является функция S(x) , опре-

делённая на этом отрезке следующим образом:
1)	S(x) f (x) ,			если			x [ l, l] и x	– точка непрерывности
функции f (x) ;
2)	S(x)	1	(f (x 0)				f (x 0)) , если	x [ l, l] и x – точка
2)	S(x)		(f (x 0)				f (x 0)) , если	x [ l, l] и x – точка
	2
разрыва первого рода функции f (x) ;
3)	S(l ) S( l )				1	(f (l 0) f ( l 0)) .
3)	S(l ) S( l )			2		(f (l 0) f ( l 0)) .
				2

Причём на любом отрезке [a, b] [ l, l] , не содержащем точек разрыва функции f (x) , тригонометрический ряд Фурье сходится равно-

мерно.

В теореме 3.3.1 сформулированы достаточные условия сходимости ряда Фурье для функции f (x) , которые называются условиями Дирихле. Из теоремы 3.3.1 следует, что значения функции f (x) в точках её разрыва первого рода не влияют на её ряд Фурье. То есть функции, имеющие одни и те же точки разрыва первого рода и отличающиеся друг от друга лишь в этих точках, разлагаются в одинаковые ряды Фурье.

Говорить о непрерывности функции на концах отрезка [ l; l] , т.е. в точках x l , вообще не имеет смысла, даже если выполняются соотношения f ( l 0) f ( l) и f (l 0) f (l ) . В самом деле, для непрерывности функции f (x) в точке x l необходимо двойное равенство f (l 0) f (l) f (l 0) . Но выражение f (l 0) характеризует поведение функции f (x) справа от рассматриваемой точки, т.е. там, где эта функция, может быть, и не определена. Это же справедливо и для f ( l 0) . Поэтому в теореме 3.3.1 концы отрезка [ l; l] играют

особую роль, сходную с ролью точек разрыва.

Заметим, что существуют и другие достаточные условия разложимости функции в тригонометрический ряд Фурье. Но для решения

практических задач обычно достаточно теоремы 3.3.1. Доказательство этой теоремы выходит за пределы данного курса, поэтому здесь не приводится.

§4. Разложение периодических функций в ряд Фурье

Напомним, функция f (x) имеет период T 0 , если для любого x из области определения этой функции справедливо равенство

f (x) f (x T) .
Все	тригонометрические функции	cos	n x	,	si n	n x
			l			l

( n 1, 2,	) определены для любого действительного значения x и

являются периодическими с периодом T 2l :

	n (x 2l )	n x					n x
cos		cos		2n	cos			,
	l		l				l

	n (x 2l )	n x				n x
si n		si n		2n	si n			.
	l		l				l

Следовательно, и любая их сумма вместе с постоянным членом

	a0	также определена для любого x и имеет период T 2l . Очевид-
	2	также определена для любого x и имеет период T 2l . Очевид-
	2

но, это свойство периодичности сохраняется и при переходе к пределу, так что сумма S(x) любого сходящегося тригонометрического ряда будет иметь период T 2l , т.е. S(x) S(x 2l) .

Подводя итог сказанному, можно сделать следующее заключение. Первоначально была задана некоторая функция f (x) , удовлетворяющая условиям Дирихле на отрезке [ l; l] . Составив её тригонометрический ряд Фурье, мы получим в качестве его суммы S(x) функцию, которая определена уже не только на отрезке [ l; l] , но и вне него. При этом на отрезке [ l; l] сумма S(x) совпадает с функцией f (x) .

Значениями функции f (x) , лежащими вне отрезка [ l; l] , мы пока просто не интересовались. В частности, функция f (x) может быть и не определена вне отрезка [ l; l] . Если предположить, что функция f (x) определена для всех x , то сумма S(x) тригонометрического ряда Фурье функции f (x) будет равна этой функции вне отрезка [ l; l] в том и только в том случае, когда сама функция f (x)

является периодической с периодом T 2l . Если же функция f (x) этим свойством не обладает, то вне отрезка [ l; l] она может не иметь ничего общего с функцией S(x) .

Пример 3.4.1. Разложить функцию f (x) x в тригонометрический ряд Фурье на отрезке [ ; ] .

Решение. Функция y x на отрезке [ ; ] удовлетворяет условиям

теоремы Дирихле. Вычислим коэффициенты тригонометрического ряда Фурье по формулам (3.5) при l

xdx

0 ,

u x

du dx

x cos nxdx

dv cos nxdx v

si n nx

si n nxdx

cosnx

u x

du dx

x si n nxdx

dv si n nxdx

cos nx

cos nxdx

cos n

cos( n )

si n nx

( 1)n 1

cos( n ) cos n ( 1)

n 1, 2,

Таким

образом, тригонометрический

ряд

Фурье

f (x) x на отрезке [ ;

] имеет вид

0 ,

функции

		1		1			n 1 1
x 2	si n x		si n 2x		si n 3x	( 1)			si n nx	.
		2		3				n

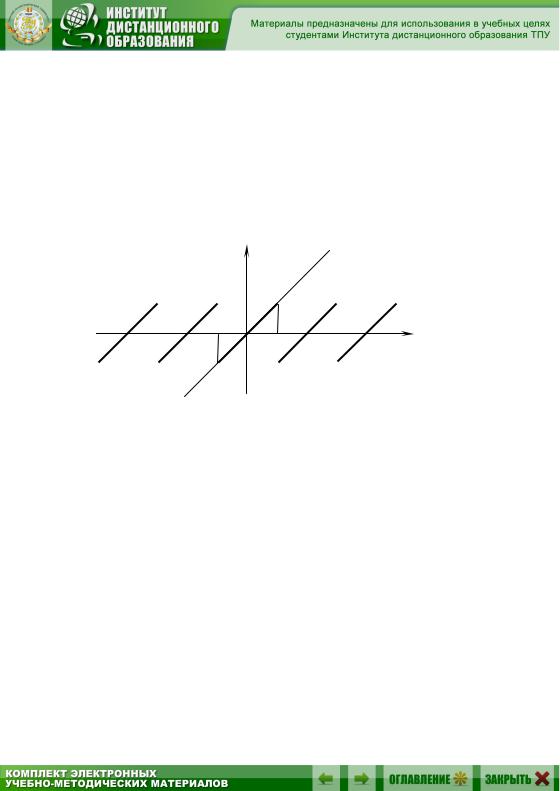
Сумма S(x) этого ряда во всех точках интервала ( ; ) совпадает с f (x) , т.е. S(x) f (x) x для всех x ( ; ) . При x сумма ряда равна нулю S( ) 0 и отличается от значений данной функции в этих точках f ( ) . Кроме того, функция S(x) является периодической с периодом T 2 . Таким образом, вне отрезка [ ; ] функция f (x) x не имеет ничего общего с суммой полученного для неё ряда Фурье. Графики функций S(x) и f (x) указаны на рисунке 3.

y	y = x

–

Рис. 3

§5. Сдвиг отрезка разложения

Поставим задачу разложить в ряд Фурье функцию на произвольном отрезке [a; b] . По существу, решение этой задачи сводится к тому, как из ортонормальной системы функций на отрезке [ l; l] получить ортонормальную систему функций на отрезке [a; b] . Переход от отрезка [ l; l] к отрезку [a; b] можно осуществить сдвигом первоначального отрезка [ l; l] вдоль оси Ox и изменением масштаба по этой оси.

Приведённая ниже лемма и основанные на ней рассуждения показывают, что сдвиги не изменяют ни ортонормальности систем периодических функций, ни соответствующих коэффициентов Фурье, если период этих функций равен длине интервала разложения.

Лемма 3.5.1. Если функция (x) периодическая с некоторым периодом T , то при любых a и имеет место равенство

a T		a T
	(x)dx		(x)dx .
a		a

Доказательство. Рассмотрим вспомогательный интеграл

a T

(x)dx

a T

	сделаем замену
	y x T, dy dx
	x a T y a
	x a T y a
	x a T y a

a	a
T )dy	(y)dy	(x)dx .
a	a

Вычислим теперь интеграл

a T

(x)dx

a T

(x)dx

(x )dx

(x )dx ,

что и

a T

требовалось доказать. ■

Поскольку функции

si n

n x

, cos

n x

при любом

n ,

как и

постоянная

являются

периодическими

функциями

периодом

T 2l , то на основании леммы 3.5.1 каждый из интегралов

n x

m x

n x

2 n x

1 dx ,

cos

si n

dx ,

si n

dx ,

cos

не изменится от сдвига его интервала интегрирования, т.е. при любом a имеют место равенства

a 2l

n x

m x

dx 1 ,

cos

si n

0 ,

1 a 2l

2 n

1 a 2l

2 n x

si n

dx 1 ,

cos

a 2l

m x

a 2l

m x

cos

si n

dx 0 , ( m n ).

Это

означает,

что система

функций

cos x ,

si n

x ,

cos

2 x

si n

2 x

,… является ортонормальной не

только на отрезке [ l; l] ,

но и на любом отрезке вида [a; a 2l] .

Если

функция f (x)

является

периодической с

периодом

T 2l ,

то

периодическими

тем

же

периодом будут функции

f (x) si n

n x

и f (x) cos

n x

Поэтому для коэффициентов

Фурье

функции f (x)

на отрезке [a; a 2l]

получим, используя лемму 3.5.1

при a l , следующие формулы:

1 a 2l

n x

1 l

n x

f (x) cos

a ,

1 a 2l

n x

1 l

n x

f (x) si n

b .

Отсюда можно сделать два вывода. Во-первых, при вычислении

коэффициентов Фурье

2l -периодической функции f (x)

на отрезке

[ l; l] можно (например, для удобства)

интегрировать не только по

этому отрезку,

а по любому другому отрезку вида [a; a 2l] , распо-

рядившись значением a так,

чтобы вычисления стали более просты-

ми. Во-вторых, при разложении 2l -периодической функции

f (x) в

ряд Фурье на отрезке [a; a 2l]

можно воспользоваться всеми теоре-

тическими утверждениями и практическими рекомендациями, которые справедливы для случая отрезка [ l; l] .

Проиллюстрируем сказанное на примере.

Пример 3.5.1. Разложить в ряд Фурье на отрезке [ ; ] функ-

цию

f (x) x 2 , если x 0, x, если 0 x .

Решение. Запишем формулы для вычисления коэффициентов Фурье заданной функции:

	1		1	0
a0		f (x)dx		(x 2 )dx xdx ,

					0

	1
an	1	f (x) cosnxdx
an		f (x) cosnxdx


	1
bn	1	f (x) si n nxdx
bn		f (x) si n nxdx

		1				0
		1				(x 2 ) cosnxdx
						(x 2 ) cosnxdx


		1				0
		1				(x 2 ) si n nxdx
						(x 2 ) si n nxdx

x cosnxdx ,
0

x si n nxdx .
0

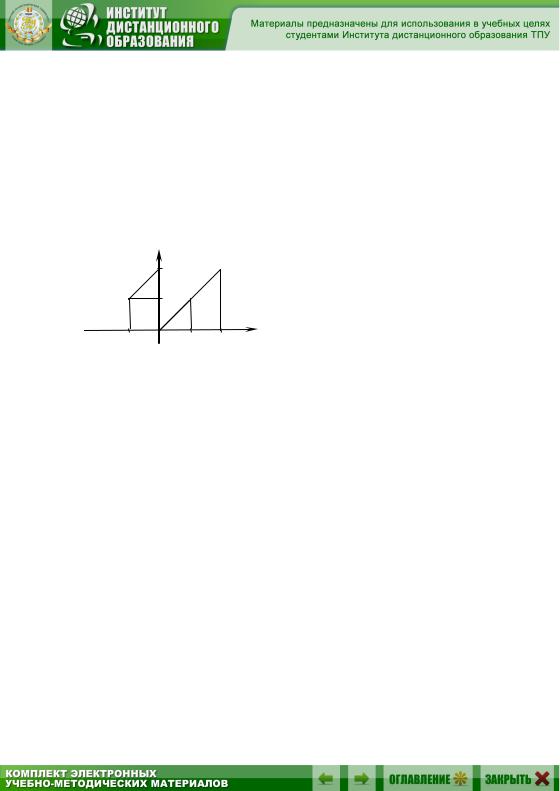
Из приведённых выражений видно, что процесс нахождения коэффициентов будет трудоёмким. Но можно заметить, что если продолжить функцию f (x) по 2 -периодичности на промежуток

( ; 2 ] , то она будет иметь достаточно простой вид f (x) x (рис. 4).

																			Для точки						x 0 эта формула не-
				y															верна, но 0 есть точка разрыва
						2													функции f (x) , так														что значение
																			функции в ней на её разложение в
																			ряд Фурье никак не влияет.
																			ряд Фурье никак не влияет.
																							Вычислим								коэффициенты
			–										2				x		Фурье:
			–										2				x						1 2						1 x 2				2
				Рис. 4																			1 2						1 x 2				2
				Рис. 4															a0					xdx									2 ,
																			a0					xdx						2			2 ,
																								0						2			0
																								0									0
	1		2										u x								du dx
	1		2										u x								du dx
an			x cos nxdx										dv cos nxdx v												1		si n nx
an			x cos nxdx																						1
			0																						n
	1		x					2			1 2											1			1							2
	1		x					2			1 2											1			1							2
				si n nx											si n nxdx												cos nx						0 ,
				si n nx											si n nxdx												cos nx						0 ,
											n														n
		n						0			n		0									n			n							0
		n						0					0																			0
	1		2									u x								du dx
bn			x si n nxdx									dv si n nxdx v														1		cosnx
bn			x si n nxdx																							1
			0																							n
		1		x						2			1		2
		1		x						2			1		2

					cos nx											cos nxdx
				n						0				n	0
										0					0
	1			2			1								2			2
	1			2			1								2			2
									si n nx										.
							n2		si n nx										.
				n			n2											n
															0

Тогда разложение в тригонометрический ряд Фурье функции f (x) на отрезке [ ; ] имеет вид

		1		1
f (x) 2	si n x		si n 2x		si n nx	.
		2		n

§6. Разложение чётных и нечётных функций в ряд Фурье
Пусть функция			f (x) задана на отрезке [ l; l] и удовлетворяет

условиям Дирихле. Рассмотрим случай, когда функция f (x) является чётной, т.е. удовлетворяет условию f ( x) f (x) . Тогда произведение

f (x) cos	n x	является чётной, а произведение f (x) si n	n x	dx явля-

	l		l

ется нечётной функциями. Из свойств определённого интеграла следует, что

l l

f (x)dx 2 f (x)dx ,

l		0
l	n x		l
f (x) cos			dx 2

l	l	0

l	n x
f (x) si n		dx 0 ,

l	l

f (x) cos n x dx . l

Запишем формулы (3.5) для коэффициентов Фурье чётной функции f (x) :

f (x)dx

f (x)dx ,

f (x) cos

n x

f (x) cos

n x

dx ,

f (x) si n

n x

dx 0 , n 1, 2,

Таким образом,

ряд Фурье чётной функции f (x) на отрезке

[ l; l]

принимает вид:

n x

f (x)

cos

(3.6)

n 1

где a

f (x)dx , a

l f (x) cos

n x

dx .

Формула (3.6) называется разложением функции f (x) в ряд по косинусам.

Рассмотрим теперь случай, когда функция f (x) является нечёт-

ной, т.е.

f ( x) f (x) ,

x [ l; l] . Тогда

n x

f (x) cos

dx 0 ,

n 0, 1, 2,

n x

f (x) si n

dx 2 f (x) si n

dx .

Следовательно, коэффициенты Фурье нечётной функции f (x)

вычисляются по формулам

f (x)dx 0 ,

f (x) cos

n x

dx 0 ,

f (x) cos

n x

2 l

f (x) cos

n x

dx , n 1, 2,

результате получаем

разложение в

ряд Фурье на

отрезке

[ l; l]

нечётной функции f (x) :

f (x) bn si n

(3.7)

n 1

где b

f (x) si n

n x

dx .

Формулу (3.7) называют разложением функции f (x)

в ряд по

синусам.

§7. Разложение в ряд Фурье функций, заданных на отрезке [0; l]

Предположим, что функция f (x) задана на отрезке [0; l] . Чтобы разложить f (x) в ряд Фурье на этом отрезке, продолжим (доопре-

делим) её на полуинтервал [ l; 0) произвольным образом. В результа-
те получим новую функцию F(x) g(x), x [ l; 0)	заданную на
f (x), x [0, l ]

отрезке [ l; l] , которую разложим в ряд Фурье на этом отрезке. Отметим, что доопределение функции на полуинтервал [ l; 0) , т.е. выбор функции g(x) , можно выполнить бесконечным множеством способов.

Так как на отрезке [0; l] функции f (x) и F(x) тождественно равны, то разложение в ряд Фурье функции F(x) является одновременно и разложением для функции f (x) на этом отрезке.

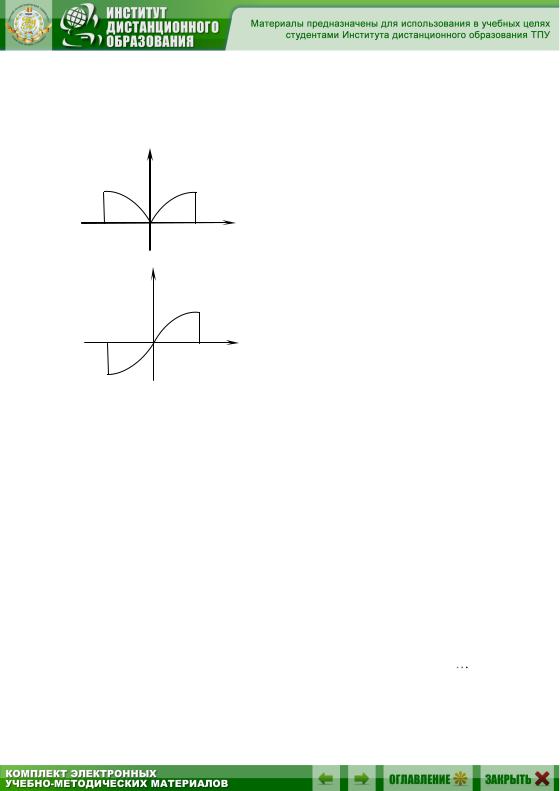
Рассмотрим два варианта доопределения функции на полуинтервале [ l; 0) , которые наиболее часто используются:

				1. Продолжение функции f (x) на
	y			полуинтервал [ l; 0) чётным образом
		y = f(x)		(рис. 5), полагая f ( x) f (x) . Тогда
				будем иметь дело с чётной функцией,
				которая разлагается в ряд по косинусам
–l	0	l	x (3.6).
	Рис. 5			2. Продолжение	функции f (x)
				2. Продолжение	функции f (x)
	y			на полуинтервал [ l; 0)	нечётным об-
		y = f(x)		разом (рис. 6), полагая	f ( x) f (x) .
				В этом случае получаем нечётную
	–l			функцию, которая разлагается в ряд по
	0	l	x	синусам (3.7).
	0	l	x	Не следует думать, что нам уда-
				Не следует думать, что нам уда-
				лось получить для одной и той же
	Рис. 6			функции два различных разложения в

ряд Фурье. В действительности мы разлагали разные функции, которые при отрицательных значениях x не имеют ничего общего между собой.

Пример 3.7.1. Разложить функцию f (x) x		на отрезке [0; ] в
ряд а) по синусам; б) по косинусам.
Решение. а) Доопределим	функцию f (x) x	на полуинтервале
[ ; 0) как нечётную. Тогда	a0 an 0 . Вычислим коэффициенты

bn :

u x

du dx

x si n nxdx

dv si n nxdx v

cosnx

cos nx

cosnxdx

cos n

2( 1)n 1

, n 1, 2,

si n nx

		Разложение функции f (x) x																							на отрезке [0; ] в тригономет-
рический ряд имеет вид
							1												1								n 1			1
x 2		si n x							si n 2x											si n 3x					( 1)						si n nx					.
x 2		si n x					2		si n 2x										3	si n 3x					( 1)					n	si n nx					.
							2												3											n
		б) Доопределим теперь функцию f (x)																									на полуинтервале [ ; 0)
как чётную. В этом случае bn																					0 . Найдём коэффициенты a0															и an :
		2							2 x				2
													2
a0			xdx													,

									2
			0						2						0
			0												0		u x								du dx
		2
		2
an			x cos nxdx														dv cos nxdx v											1		si n nx
an			x cos nxdx																									1
			0																									n
		2	x												1										2		1


						si n nx													si n nxdx										cosnx
						si n nx													si n nxdx										cosnx
																n									n		n
			n								0					n	0								n		n							0
			n								0						0																	0
		2			( 1)			n	1								0,				если n чётное,

		n		2																	если n		нечётное.
		n															2,				если n		нечётное.
		Таким образом,																разложение						функции						f (x) x					на отрезке
[0; ]		в ряд Фурье имеет вид
x			4							1				cos3x							1								1				cos(2n 1)x
					cos x																	cos5x															.
	2				cos x							2									2	cos5x				(2n 1)						2					.
	2									3										5						(2n 1)

§8. Физическая интерпретация разложения функции в тригонометрический ряд Фурье

Тригонометрические ряды используются при изучении периодических функций, математически описывающих различные повторяющиеся процессы, происходящие в природе и технике. Примерами таких процессов являются колебательные и вращательные движения различных деталей машин, приборов, периодическое движение небесных тел и элементарных частиц, акустические и электромагнитные колебания и др.

Будем в качестве независимого переменного x функции f (x) рассматривать время. Тогда функциональная зависимость опишет некоторый происходящий во времени процесс. Ограничимся случаем, когда этот процесс сводится к механическим движениям некоторой системы, т.е. к её пространственным перемещениям.

Возникает вопрос о представлении движения на некотором отрезке времени в виде комбинации тех или иных заранее заданных движений. Этому представлению движения будет соответствовать разложение описывающей его функции в функциональный ряд по заданным функциям. В частности, можно поставить вопрос о представлении достаточно произвольного движения на некотором отрезке времени

[0; l] в виде гармонических колебаний с периодами 2l ,				2l	,	2l	,…
[0; l] в виде гармонических колебаний с периодами 2l ,				2	,	3	,…
				2		3
Так	как	любое колебание такого вида представляется выражением
	n t
An	si n		n , то ему соответствует пара членов тригонометри-
An	si n	l	n , то ему соответствует пара членов тригонометри-
		l

ческого ряда	a	cos	n t	b	si n	n t	, где	a	A	si n ,

	n		l	n		l		n	n	n

bn An cos n .

Таким образом, пара соседних членов тригонометрического ряда соответствует некоторой гармонической составляющей общего

движения системы с периодом T 2l и амплитудой A . Эта гармо-

n	n

ническая составляющая обычно называется n -ой гармоникой движе-

ния.	Очевидно,		что амплитуда n -ой гармоники вычисляется по фор-
муле	A	a 2	b 2 .
	n	n	n

Вопросы и задания для самопроверки

1. Проверьте, выполняются ли условия Дирихле для функции

f (x) 2, если x 0,, если 0 x .

2. Задана функция
f (x) 1, если 3		x 0,
2, если	0	x	3.
Найдите значения S(1) , S( 4) , S(3) ,	S(0) ,		S(6) суммы ряда Фурье
этой функции.

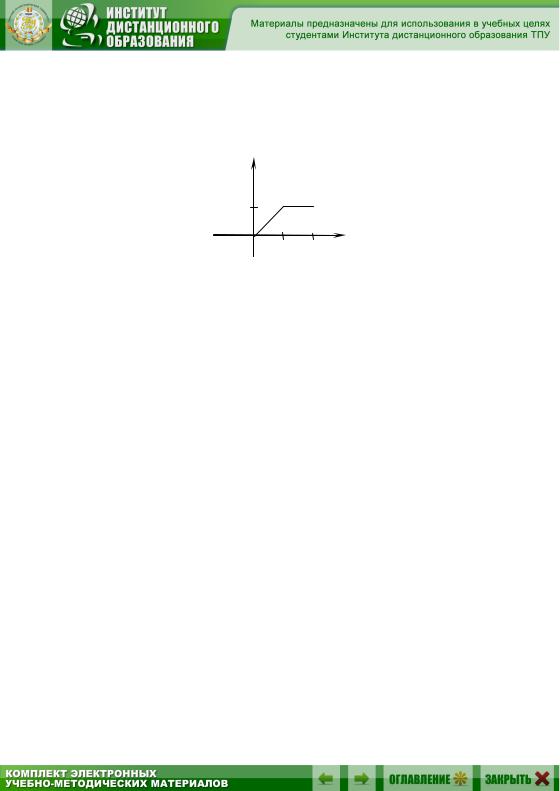
3. Функция f (x) задана графически на интервале (0; 2) . Запишите, не вычисляя, формулы для коэффициентов в разложении f (x) в ряд по синусам. Постройте график суммы ряда Фурье функции f (x) .

0	1	2	x

Рис. 7

4. Запишите формулы для коэффициентов Фурье функций на указанных отрезках:

а) y x	2	1 ,	1	;	1	;	б) y \| x \| x , [ 1; 1] .
			2		2

5. Будет ли ортогональной система функций x , x 3 , x 5 ,…, x 2k 1 ,… на отрезке [ l; l] ?

6. Функции 1 (x) и 2 (x) ортогональны на отрезке [a; b] . Следует ли из этого факта их ортогональность на отрезке [c; d] [a; b] ?

7. На каком из отрезков [0; 2] или [ 1; 1] ортогональны функции x 2 , x 3 ?

8. Ряды Фурье для функций f1 (x) и f2 (x)								совпали. Следует ли из этого
факта, что f1 (x) = f2 (x) ?
9. Можно ли функцию
			1, если 2					x 0,
				1
			f (x )	1	, если		0 x 2
					, если		0 x 2
				x
разложить в ряд Фурье на отрезке [ 2; 2] ?
10. На отрезке [0; l] задана функция							f (x) 2x . Запишите формулы
для вычисления коэффициентов Фурье в случае, если:
а)	T 2l	и f (x)	на отрезке [ l; 0)			доопределена чётным образом;
б)	T 2l	и f (x)	на отрезке [ l; 0)			доопределена нечётным образом;
в) T l ;
г)	T 2l	и f (x) 0 на отрезке [ l; 0) . Сделайте чертежи.

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
29.05.2015436.74 Кб151UMP_BisnessPlan.doc
#
10.11.201916.52 Mб16UNITS.doc
#
29.05.20152.91 Mб50up-part2.pdf
#
29.05.20157.8 Mб78up.pdf
#
29.05.20151.9 Mб19up.pdf
#
29.05.20151.8 Mб14up_2.pdf
#
25.03.20161.09 Mб18UP_EST_CH1.pdf
#
29.05.20151.43 Mб163UP_Metody.pdf
#
04.11.2018108.54 Кб5Urok_po_Word.doc
#
29.05.20151.85 Mб46Using External Code in LabVIEW.pdf
#
22.11.2019295.94 Кб6ustav.doc