

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное учреждение высшего профессионального образования
«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
___________________________________________________
Е.А. Молдованова, А.Н. Харлова
ВЫСШАЯ МАТЕМАТИКА
РЯДЫ
Учебное пособие
Рекомендовано к печати Редакционно-издательским советом Томского политехнического университета
Издательство Томского политехнического университета
2009
1

УДК 517.52 ББК 22.161я73
|
М 75 |
|
Молдованова Е.А. |
|
Высшая математика. Ряды: учебное пособие /А.Н. Харло- |
М 75 |
ва. – Томск: Изд-во Томского политехнического универ- |
|
|
|
ситета, 2009. – 83 с. (В авторской редакции) |
В пособии изложен материал по общему курсу высшей математики, раздел «Ряды», в объёме, предусмотренном действующей программой для студентов технических вузов.
Материал пособия излагается в логической последовательности и сопровождается примерами, облегчающими процесс усвоения теоретических положений курса.
Пособие адресуется студентам второго курса ИДО.
УДК 517.52 ББК 22.161я73
Рецензент
Кандидат физико-математических наук, Доцент кафедры высшей математики ТГАСУ
Шалыгина Т.А.
Е.А. Молдованова, А.Н. Харлова, 2009
Томский политехнический университет, 2009
2

ОГЛАВЛЕНИЕ |
|
Предисловие............................................................... |
4 |
Введение.................................................................... |
4 |
Глава 1. ЧИСЛОВЫЕ РЯДЫ........................................ |
6 |
§1. Основные понятия............................................... |
6 |
§2. Свойства сходящихся числовых рядов .................. |
8 |
§3. Необходимый признак сходимости........................ |
10 |
§4. Достаточные признаки сходимости....................... |
12 |
§5. Знакочередующиеся ряды.................................... |
21 |
Вопросы и задания для самопроверки........................... |
26 |
Глава 2. ФУНКЦИОНАЛЬНЫЕ РЯДЫ.......................... |
28 |
§1. Определение функционального ряда...................... |
28 |
§2. Равномерная сходимость функциональных рядов... |
31 |
§3. Свойства равномерно сходящихся рядов................ |
34 |
§4. Степенные ряды.................................................. |
38 |
§5. Свойства степенных рядов.................................... |
44 |
§6. Разложение функций в степенные ряды................ |
46 |
§7. Разложение основных элементарных функций в ряд Маклоре- |
|
на............................................................... |
50 |
§8. Применение степенных рядов............................... |
57 |
Вопросы и задания для самопроверки........................... |
62 |
Глава 3. РЯДЫ ФУРЬЕ............................................... |
63 |
§1. Ортогональные системы функций......................... |
64 |
§2.Тригонометрические ряды Фурье........................... |
66 |
§3. Достаточные условия разложения функции в ряд Фу- |
|
рье.......................................................................... |
69 |
§4. Разложение периодических функций в ряд Фурье.. |
70 |
§5. Сдвиг отрезка разложения................................... |
72 |
§6. Разложение чётных и нечётных функций в ряд Фурье |
|
.............................................................................. |
76 |
§7. Разложение в ряд Фурье функций, заданных на отрезке |
|
[0, l] ................................................................... |
77 |
§8. Физическая интерпретация разложения функции в тригономет- |
|
рический ряд Фурье................................ |
79 |
Вопросы и задания для самопроверки........................... |
80 |
Литература................................................................. |
82 |
3

ПРЕДИСЛОВИЕ
Настоящее учебное пособие предназначается студентам ИДО. В нём излагается материал раздела высшей математики «Ряды».
В главе I рассматриваются числовые ряды, а главы II, III посвящены функциональным рядам.
Пособие имеет следующую структуру. В нём содержатся основные определения, формулировки и доказательства теорем и следствий из них. Начало доказательств теорем, следствий и свойств обозначено
символом , а конец – ■. Кроме того, приводятся примеры решения задач, иллюстрирующие теоретический материал, а также вопросы и задания для самопроверки.
Учебное пособие составлено с учётом того, что студенты вынуждены изучать курс самостоятельно.
Авторы
ВВЕДЕНИЕ
Бесконечные ряды вошли в математическую практику в XVII веке в процессе становления дифференциального и интегрального исчислений.
Следует отметить, что ряды при их изучении доставляют трудности, связанные с необычностью самого объекта изучения, которым является ряд, т.е. сумма бесконечного числа слагаемых. Простой пример позволяет наглядно изобразить такую сумму.
Возьмём отрезок длины 2. Разделим его на два равных отрезка, каждый длины 1. Не трогая левого отрезка, разделим правый на два равных отрезка, каждый длины 1/2. Правый из них разделим на два отрезка, каждый длины 1/4. Продолжим этот процесс до бесконечно-
1 |
1/2 |
1/4 |
1/8 |
сти.
Тогда длина исходного отрезка может быть выражена как сум-
ма:
2 1 |
1 |
|
1 |
|
1 |
|
|
1 |
|
( ) |
|
2 |
4 |
8 |
16 |
||||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
4 |
|

Приведённое рассуждение было известно ещё грекам, а философ Зенон оспаривал его законность. Зенон известен своими «парадоксами». Один из этих парадоксов утверждает, что бегущий человек никогда не сможет достичь своей цели, поскольку он должен сначала пробежать половину требуемой дистанции, затем половину оставшейся части и т.д. Таким образом, он должен пробежать бесконечное множество расстояний, а это будет продолжаться вечно.
Конечно, все мы видели бегунов, достигавших финиша. Но этот пример показывает, что сложение бесконечного множества чисел нельзя толковать как процесс, аналогичный сложению конечного их числа. Если мы попытаемся вычислить бесконечную сумму, такую как, например, ( ), последовательно выполняя все заданные в ней сложения, то это никогда не закончится. Тем не менее, интуитивно мы чувствуем, что равенство ( ) верное.
Такие противоречия долгое время не позволяли математикам создать стройную математическую теорию. Только в XIX веке ряды стали предметом изучения сами по себе и в настоящее время широко используются при решении различных задач, в доказательствах теорем, получениях асимптотических оценок и т.п.
5

Глава 1. ЧИСЛОВЫЕ РЯДЫ
§1. Основные понятия
Пусть дана бесконечная числовая последовательность u1 , u2 ,
u3 ,…, un ,…
Определение 1.1.1. Числовым рядом называется выражение ви-
да
|
|
|
u1 u2 |
un |
un , |
|
|
n 1 |
а элементы последовательности u1 , u2 , |
u3 ,…, un ,… называются чле- |
|
нами ряда. |
|
|
Для задания ряда необходимо задать каждый его член. Обычно он записывается как некоторая функция от своего номера un f (n) .
Аналитическое выражение этой функции называют общим членом ряда. Например, общим членом ряда
1 13 51 71 
является выражение un |
1 |
|
. |
|
|
|
|||
2n 1 |
||||
|
|
|||
Определение 1.1.2. Сумма n первых членов ряда
вается n -ой частичной ( n -частичной) суммой этого ряда
|
n |
sn u1 u2 |
un uk . |
|
k 1 |
un назы-
n 1
Частичные суммы ряда образуют бесконечную числовую последовательность
s1 |
u1 , |
|
s2 |
u1 u2 , |
|
s3 |
u1 u2 u3 , |
|
……………………… |
|
|
|
|
|
|
Определение 1.1.3. Ряд un |
называется сходящимся, если по- |
|
n 1 |
|
следовательность его частичных сумм имеет конечный предел |
||
|
l i m sn |
s . |
|
n |
|
|
6 |
|

Значение s этого предела называется суммой ряда.
Определение 1.1.4. Ряд un называется расходящимся, если
n 1
последовательность его частичных сумм расходится (т.е. l i m sn не
n
существует или равен бесконечности).
Рассмотрим несколько примеров выяснения сходимости или расходимости ряда по определению.
Пример 1.1.1. Исследовать на сходимость ряд
1 2 3 n
Решение. Члены данного ряда образуют арифметическую прогрессию
|
|
|
|
|
|
|
|
|
|
с разностью d 1 |
и a1 1 . Поэтому n -частичная сумма ряда |
n |
|||||||
|
|
|
|
|
|
|
|
|
n 1 |
имеет |
|
вид |
|
s 1 2 3 |
n |
n(n 1) |
|
и |
|
|
|
||||||||
|
|
|
|
n |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
n(n |
1) |
|
|
|
|
||
l i m sn |
l i m |
. Следовательно, |
ряд n расходится. |
|
|||||
2 |
|
|
|||||||
n |
n |
|
|
|
n 1 |
|
|||
|
|
|
|
|
|
|
|||
|
Пример 1.1.2. Исследовать на сходимость ряд |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 1 1 |
( 1)n 1 . |
|
||||
|
|
|
|
|
n 1 |
|
|
|
|
Решение. Для данного ряда всякая частичная сумма sk с чётным номером равна 0, а всякая сумма с нечётным номером равна 1. Последо-
вательность частичных сумм этого ряда s1 1 , |
s2 0 , |
s3 1 , |
s4 0 , … хотя и ограничена, но предела не имеет. Значит, ряд расхо-
дится.
Пример 1.1.3. Исследовать на сходимость ряд
|
|
b1 b1q b1q2 |
b1qn . |
|
n 0 |
Решение. Данный ряд составлен из элементов геометрической про-
грессии с первым членом b1 |
и знаменателем q . Тогда сумма n пер- |
|||||||
вых членов ряда имеет вид |
|
|
|
|
|
|
||
s b b q b q2 |
|
b qn 1 |
b (1 qn ) |
|
||||
1 |
|
, q 1 . |
||||||
|
|
|||||||
n |
1 1 |
1 |
|
|
1 |
1 |
q |
|
|
|
|
|
|
|
|
||
Заметим, что |
|
|
|
|
|
|
|
|
|
|
li m qn |
|
0, |
если | q | 1, |
|
||
|
|
|
если | q | 1, |
|
||||
|
|
n |
|
, |
|
|||
|
|
|
|
|
|
|
|
|
7

поэтому
l i m s l i m |
b (1 qn ) |
|
b |
|||
1 |
|
1 |
||||
|
|
|
||||
n |
n |
n |
1 q |
|
|
1 q |
|
|
|
||||
|
|
Если |
q 1 , |
|
то |
|
sn b1 b1 b1 |
b1 nb1 |
|||||
n штук
|
|
b1 |
, если | q | 1, |
|
n |
|
|
|
|
|
q |
|||
l i m(1 q ) 1 |
|
|||
n |
|
|
если | q | 1. |
|
|
|
|||
|
, |
|||
n -частичная |
|
сумма |
имеет вид |
|
и li m s li m b n b li m n . |
||||
n n |
n |
1 |
1 |
n |
|
|
Если |
q 1 , |
то |
n -частичная |
сумма |
имеет |
вид |
||||
sn |
b1 |
b1 |
b1 |
b1 b1 (1 1 |
1) . |
При чётном |
n 2k |
|||||
|
|
|
|
n штук |
|
|
|
|
|
|
|
|
s2k |
0 |
и |
li m s2k |
0 . |
При |
нечётном |
n 2k 1 |
s2k 1 |
1 |
и |
||
|
|
|
|
k |
|
|
|
|
|
|
|
|
li m s2k 1 1 . Это означает, что l i m sn |
не существует. |
|
|
|
||||||||
k |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, ряд b1qn сходится при | q | 1 |
и его сумма |
|||||||||
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
равна |
|
b1 |
; при | q | 1 |
он расходится. |
|
|
|
|
||||
1 q |
|
|
|
|
||||||||
|
|
Определение 1.1.5. Выражение вида |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rn un 1 un 2 |
um , |
|
|
|
|||
m n 1
представляющее собой числовой ряд, называется n -ым остатком
|
|
|
|
ряда un . |
|
|
|
n 1 |
|
|
|
|
|
|
|
Очевидно, что un |
sn rn . |
|
|
n 1 |
|
|
|
§2. Основные свойства сходящихся числовых рядов |
|
|
|
|
|
|
|
Свойство 1. Если ряд un сходится, то и его остаток |
rn |
um |
|
n 1 |
|
|
m n 1 |
сходится.
Действительно, все частичные суммы остатка отличаются на одну и ту же постоянную величину C от соответствующих частичных сумм
8

ряда. А из сходимости последовательности (sn ) следует сходимость последовательности (sn C) .■
Из этого свойства следует, что на сходимость (расходимость) ряда не влияет отбрасывание любого конечного числа первых членов или наоборот присоединение конечного числа членов.
|
|
|
|
|
|
|
Свойство 2. Если ряд |
un |
сходится и его сумма равна s , то ряд |
||||
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
cun |
также сходится и cun cs , где c 0 , c const . |
|||||
n 1 |
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
Действительно, |
n -частичная |
сумма ряда cun имеет вид |
||||
|
|
|
|
|
|
n 1 |
|
|
|
n |
|
n |
|
sn cu1 cu2 |
cun cuk |
c uk , поэтому |
||||
|
|
|
k 1 |
|
k 1 |
|
|
n |
|
n |
|
|
|
li m sn |
li m c uk |
c li m uk cs .■ |
|
|||
n |
n k 1 |
|
n k 1 |
|
|
|
|
|
|
|
|
|
|
Свойство 3. Если ряды |
un |
и |
vn |
сходятся и их суммы, соответ- |
||
|
|
|
n 1 |
|
n 1 |
|
|
|
|
|
|
|
|
ственно, равны su |
и sv , то ряд |
(un |
vn ) также сходится, причём |
|||
n 1
его сумма равна su sv .
Действительно,
n |
n |
n |
|
|
li m (uk |
vk ) li m uk vk |
|
||
n k 1 |
n k 1 |
k 1 |
|
|
su sv . ■
n |
n |
li m uk |
li m vk |
n k 1 |
n k 1 |
Из свойств 2 и 3 следует, что сходящиеся ряды можно почленно умножать на число c 0 , складывать, вычитать, так же, как это делается обычно с суммами конечного числа слагаемых.
Установление факта сходимости числового ряда по определению, с помощью частичных сумм, является достаточно трудоёмкой задачей. При изучении рядов значения частичных сумм не представляют интереса, зачастую важен лишь факт сходимости или расходимости ряда. Ниже рассмотрим теоремы, позволяющие этот факт установить.
9

§3. Признаки сходимости числовых рядов
Теорема 1.3.1 (необходимый признак сходимости ряда). Если
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ряд un сходится, то предел его общего члена равен нулю |
|
||||||||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
li m un 0 . |
|
|
|
|
|
||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||
|
Доказательство. |
Рассмотрим |
n -частичную |
сумму |
ряда |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sn u1 u2 |
un |
sn 1 |
un . |
Если |
ряд |
un |
сходится, |
то |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
li m sn |
li m sn 1 |
s . Но тогда |
|
|
|
|
|
|
|
|
|
|
|
||||
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
li m sn |
li m(sn 1 |
un ) li m sn 1 li m un . |
|
|||||||||||||
|
n |
n |
|
|
|
|
|
|
n |
n |
|
|
|||||
Таким образом, |
s s li m un . |
Откуда получаем li m un |
0 . ■ |
|
|||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
Пример 1.3.1. Исследовать на сходимость гармонический ряд |
||||||||||||||||
|
|
|
1 |
|
1 |
|
1 |
|
1 |
|
|
|
|||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
n |
2 |
|
3 |
n |
|
|
|||||||||
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Очевидно, что для гармонического ряда выполняется необ-
ходимый признак сходимости l i m 1 0 . Тем не менее, ряд расходит-
n n
ся. Докажем это. Предположим, что гармонический ряд сходится. Обозначим его сумму через S . Тогда получим, что
li m(s2n |
sn ) li m s2n |
li m sn S S 0 . |
n |
n |
n |
Но с другой стороны |
|
|
s |
s |
|
|
1 |
|
1 |
|
|
1 |
|
1 |
|
1 |
|
|
1 |
n |
1 |
|
1 |
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
2n |
|
n |
n |
1 |
n 2 |
|
2n 2n 2n |
|
2n |
|
|
2n 2 |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
То есть для всех номеров |
n выполняется неравенство |
s |
s |
|
1 |
. |
||||||||||||||||||||||
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
|
n |
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отсюда следует, что равенство li m(s2n sn ) 0 |
невозможно. Следо- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
вательно, гармонический ряд расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Пример 1.3.2. Установить расходимость следующих рядов: а) |
||||||||||||||||||||||||||
|
|
2n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n |
|
|
|
|
|
|
|||||
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
б) 1 |
|
. |
|
|
|
|
|||||||
|
5n 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
n |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

Решение. а) Ряд 2n 1 расходится, так как не выполняется не- n 1 5n 6
обходимый признак
|
|
|
|
1 n |
||
б) Ряд |
1 |
|
|
|
||
n |
||||||
n 1 |
|
|
|
|
||
|
|
|
|
|
||
l i m |
2n 1 |
|
2 |
0 . |
|
5n 6 |
5 |
||||
n |
|
|
расходится, так как
|
|
|
|
1 n |
e 0 . |
||
l i m |
1 |
|
|
||||
n |
|||||||
n |
|
|
|
|
|
||
|
|
|
|
|
|
||
Заметим, что условие li m un 0 не является достаточным для
n
сходимости ряда. Например, ряд 1 расходится (пример 1.3.1), хо-
n 1 n
тя для него необходимый признак выполняется li m |
1 |
0 . Однако, |
|
||
n n |
|
|
если для некоторого ряда имеем li m un 0 , то на основании теоремы
n
1.3.1 можно сказать, что ряд расходится. Если же li m un 0 , то о схо-
n
димости ряда ничего сказать нельзя, – необходимо дополнительное исследование, которое может быть проведено с помощью достаточных признаков.
Таким образом, приведённый признак сходимости следует понимать так:
|
|
|
|
Если li m un 0 |
(или не существует), то ряд un |
расходится. |
|
n |
|
n 1 |
|
|
|
|
|
|
|
|
|
Но если li m un 0 , то ряд |
un может как сходиться, |
так и расхо- |
|
n |
|
n 1 |
|
|
|
|
|
диться.
Теорема 1.3.2. Если ряд сходится, то последовательность его частичных сумм ограничена.
Доказательство. Пусть ряд un сходится. Тогда по опреде-
n 1
лению 1.1.3 предел последовательности его частичных сумм sn существует и равен конечному числу, а это и означает, что последовательность sn ограничена. ■
Заметим, что ограниченности последовательности частичных сумм ряда ещё не достаточно для его сходимости, так как ограниченности последовательности недостаточно для её сходимости. Например,
11

ряд ( 1)n 1 расходится (см. пример 1.1.2), хотя последовательность
n 1
частичных сумм этого ряда ограничена |sn | 2 при любом n .
§4. Достаточные признаки сходимости числовых рядов с положительными членами
Определение 1.4.1. Числовой ряд un называется знакопо-
n 1
ложительным, если его члены положительны, т.е. un 0 .
Теорема 1.4.1 (интегральный признак). Пусть дан ряд un ,
n 1
члены которого являются значениями функции, удовлетворяющей условиям:
1)f (x) f (n) при x n ;
2)f (x) 0 для x [1, ) ;
3)f (x) монотонно убывает при x [1, ) ;
4) f (x) непрерывна при x [1, ) .
Тогда несобственный интеграл f (x)dx и числовой ряд
1
un сходятся или расходятся одновременно.
n 1
Доказательство. Так как функция f (x) непрерывна и убывает, то для справедливо неравенство f (k) f (x) f (k 1) . Проинтегрируем последнее неравенство в пределах от k до k 1
k 1 |
k 1 |
k 1 |
|||
|
f (k)dx |
|
f (x)dx |
|
f (k 1)dx , |
k |
|
k |
|
k |
|
или, учитывая f (k) uk , получим
k 1
uk f (x)dx uk 1 .
k
12

|
Запишем последние неравенства для k 1, |
, n : |
|
|
||||
|
2 |
|
|
|
|
|
|
|
|
u1 f (x)dx u2 , |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
u2 f (x)dx u3 , |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
………………………… |
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
un |
f (x)dx un 1 . |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
Просуммировав их, найдём sn |
|
f (x)dx sn 1 |
u1 . |
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
интеграл f (x)dx |
сходится и |
равен |
I, тогда |
|||
|
|
1 |
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
f (x)dx I |
и sn 1 I u1 |
C |
или |
sn 1 un |
sn |
C |
n . |
1 |
|
|
|
|
|
|
|
|
Таким образом, монотонно возрастающая последовательность частич-
ных сумм sn |
ограничена сверху и, следовательно, сходится. А это оз- |
||||
|
|
|
|
|
|
начает сходимость ряда un |
. Наоборот, если сходится ряд un , то |
||||
|
|
n 1 |
|
|
n 1 |
последовательность его частичных сумм sn |
ограничена. Поэтому ог- |
||||
раничена |
и |
сходится монотонно возрастающая последовательность |
|||
|
|
|
|
n 1 |
|
определённых интегралов I n 1 |
f (x)dx , |
т.е. сходится несобствен- |
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
ный интеграл f (x)dx . |
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
Пусть теперь интеграл |
f (x)dx расходится. Тогда в силу нера- |
||||
|
|
|
1 |
|
|
|
|
n 1 |
|
|
|
венства sn |
|
f (x)dx последовательность частичных сумм sn неог- |
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
раничена, |
а значит, ряд un |
расходится. |
Если же расходится ряд |
||
n 1
13

un , то последовательность его частичных сумм неограничена, тем
n 1
|
|
n 1 |
|
более, неограничена последовательность I n 1 |
|
|
f (x)dx . Значит, |
|
|
1 |
|
интеграл f (x)dx расходится. Теорема доказана. ■
1
Пример 1.4.1. С помощью интегрального признака исследовать на сходимость обобщённый гармонический ряд
n1p .
n 1
Решение. Рассмотрим функцию f (x ) x1p ( x 1 ). Она удовлетворя-
ет всем условиям теоремы 1.4.1 при p 0 . Пусть p 1 , тогда
|
|
|
dx |
|
p |
|
|
x |
p 1 |
|
b |
1 |
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
f (x)dx |
|
|
|
|
x |
|
dx |
li m |
|
|
|
|
|
li m |
|
|
1 |
|
|
||||
|
|
p |
|
|
|
|
|
b 1 |
|||||||||||||||
|
|
|
p 1 |
|
|||||||||||||||||||
1 |
|
|
1 |
x |
|
|
1 |
|
|
b |
|
1 |
p 1 b x |
|
|
|
|
||||||
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
. В этом случае значение интеграла есть конечное |
||||||||||||||||||
|
|
|
|
||||||||||||||||||||
p 1 |
|
p 1 |
|||||||||||||||||||||
число, т.е. интеграл сходится, а значит, и ряд сходится.
Если 0 p 1 , имеем |
|
f (x)dx |
dx |
|
1 |
li m |
|
x1 b 1 |
|
|
и |
|
|
|
|
|
|||||||||
|
x p |
|
||||||||||
|
|
|
p 1 b |
|
|
|
||||||
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
несобственный интеграл расходится, следовательно, и ряд расходится. При p 0 обобщённый гармонический ряд расходится, так как не выполняется необходимый признак сходимости (теорема 1.3.1).
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1.4.2. Исследовать на сходимость ряд |
1 |
. |
|||||||
|
n l n n |
|||||||||
|
|
|
|
|
|
|
|
n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
Решение. Функция f (x) |
|
|
при x 2 удовлетворяет условиям |
|||||||
x l n x |
||||||||||
теоремы 1.4.1. Рассмотрим несобственный интеграл |
|
|
||||||||
|
|
dx |
|
d(ln x) |
|
|
b |
|
|
|
f (x)dx |
|
li m ln | ln x | |
2 |
|
|
|||||
x ln x |
|
|
|
|||||||
2 |
2 |
2 |
ln x |
b |
|
|
||||
|
|
|
|
|
|
|
|
|
||
= li m ln | ln b | ln | ln 2 | .
b
14

Поскольку интеграл расходится, то и исследуемый ряд также расходится.
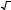
Пример 1.4.3. Исследовать на сходимость ряд e n .
n 1  n
n
Решение. Функция |
f (x) |
e |
|
|
x |
|
при x 1 удовлетворяет условиям |
||||||||||||||
|
|
|
|
|
|
||||||||||||||||
x |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
теоремы 1.4.1. Вычисляя несобственный интеграл |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
|
|
|
|
|
|
|
|
|||||||||||||
f (x)dx |
e |
|
|
dx |
2 e |
x |
d( x ) 2 l i m e x |
|
b |
||||||||||||
|
|
|
|
|
|
||||||||||||||||
1 |
1 |
|
|
|
|
x |
1 |
|
|
|
|
|
|
b |
|
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 li m e |
|
|
e 1 |
|
|
|
|||||||||||||||
b |
2 ( e 1 ) 2e 1 , получили |
|
конечное число |
||||||||||||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
( 2e 1 |
), следовательно, несобственный интеграл сходится, значит, |
||||||||||||||||||||
и исследуемый ряд сходится. |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 1.4.2 |
(первый признак сравнения). Пусть un и |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
vn |
два знакоположительных ряда, причём члены первого, начиная |
||||||||||||||||||||
n1
снекоторого номера k , не превосходят соответствующих членов второго:
un vn , n k, k 1,
Тогда
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) из сходимости ряда vn |
следует сходимость ряда |
un |
; |
|
|
||||||||
|
|
|
|
n 1 |
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) из расходимости ряда un |
следует расходимость ряда vn . |
||||||||||||
|
|
|
|
n 1 |
|
|
|
|
n 1 |
|
|
||
Доказательство. Предположим сначала, что k 1 . |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) Пусть ряд |
|
v |
n |
сходится. Обозначим через s |
и |
s |
n |
-частичные |
|||||
|
|
|
|
n |
n |
|
|
|
|
|
|||
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
суммы рядов un |
и vn |
соответственно. Из условия теоремы сле- |
|||||||||||
|
n 1 |
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дует неравенство |
s |
s n |
. А из сходимости ряда |
|
v |
n |
следу- |
||||||
|
|
|
n |
n |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
ет ограниченность последовательности s , а значит, |
и последователь- |
||||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|

ности sn . Заметим, что последовательность частичных сумм ряда яв-
ляется монотонной, поэтому из ограниченности последовательности
sn вытекает сходимость ряда un .
|
|
|
n 1 |
|
|
|
|
|
|
2) Пусть ряд |
un |
расходится. Тогда последовательность sn |
неогра- |
|
|
n 1 |
|
|
|
ничена, следовательно, |
неограничена и последовательность |
s , зна- |
||
|
|
|
|
n |
|
|
|
|
|
чит, ряд vn расходится. |
|
|||
n 1 |
|
|
|
|
Если |
k 1 , |
то |
для доказательства теоремы достаточно рас- |
|
|
|
|
|
|
смотреть ряды un и |
vn , так как отбрасывание конечного числа |
|||
|
n k |
|
n k |
|
членов ряда не влияет на его сходимость. ■ Проиллюстрируем применение первого признака сравнения на
примере.
Пример 1.4.4. Исследовать на сходимость ряд
|
|
|
|
2n |
|
|
|||||
|
|
|
|
cos2 n |
. |
|
|
||||
|
|
n 1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
cos2 n |
|
1 |
|
|
|
|
|
cos2 n |
|
|
Решение. Поскольку |
|
|
|
|
|
, то члены ряда |
|
меньше |
|||
2n |
|
2n |
|
2n |
|||||||
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|||||
соответствующих членов ряда |
|
|
1 |
, составленного из членов гео- |
|||||||
|
2n |
||||||||||
|
|
|
|
n 1 |
|
|
|||||
метрической прогрессии со знаменателем q 12 1 . Сходимость это-
го ряда была установлена в примере 1.1.3. Поэтому на основании тео-
ремы 1.4.2 ряд cos2 n сходится.
n 1
2n
Теорема 1.4.3 (второй или предельный признак сравнения).
Если существует конечный, отличный от нуля предел
|
l i m |
un |
C 0 , |
|
|
||
|
n v |
|
|
|
|
n |
|
|
|
|
|
то оба ряда un |
и vn сходятся или расходятся одновременно. |
||
n k |
n k |
|
|
16

|
Доказательство. Из определения предела l i m |
un |
C следу- |
|||||
|
|
|||||||
|
|
|
|
|
n v |
|
||
|
|
|
|
|
|
n |
|
|
ет, |
что для любого положительного , например 0 C , |
найдётся |
||||||
номер n0 , такой, что |
C un / |
vn C |
n n0 или, |
так как |
||||
vn |
0 , |
(C )vn un |
(C )vn |
n n0 . |
Из сходимости ряда |
|||
|
|
|
|
|
|
|
|
|
vn согласно свойству 2 числовых рядов (§2) следует сходимость |
||||||||
n k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ряда (C )vn , а значит, по теореме 1.4.2 ряд un сходится. Если |
||||||||
|
n k |
|
|
|
n k |
|
||
|
|
|
|
|
|
|
||
ряд |
vn |
расходится, |
то расходится и ряд (C )vn и, |
следова- |
||||
|
n k |
|
|
n k |
|
|||
тельно, ряд un также расходится.
n k
Аналогично доказывается, что из сходимости (расходимости)
|
|
ряда un |
следует сходимость (расходимость) ряда vn .■ |
n k |
n k |
При применении признаков сравнения данный ряд сопоставляется с одним из рядов, сходимость которых уже установлена заранее. В качестве таких известных рядов обычно используются эталонные ряды:
обобщенный гармонический ряд (пример 1.4.1);
ряд, составленный из членов геометрической прогрессии
(пример 1.1.3).
Результаты исследования эталонных рядов приведены в табл. 1.
|
|
|
|
Таблица 1 |
|
|
р |
сх |
рас- |
|
|
яд |
|
|
одится |
ходится |
|
|
|
|
|
|
|
b1qn |
| q | 1 |
| q | 1 |
|
||
n 0 |
|
|
|
|
|
|
|
|
|
|
|
n p |
|
|
|
||
|
1 |
|
p 1 |
p 1 |
|
n 1 |
|
|
|
||
|
|
|
|
|
|
17

|
Пример 1.4.5. Исследовать на сходимость ряд |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
2 n n2 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. Общий член данного ряда un |
|
1 n |
|
|
эквивалентен |
||||||||||||||||||||||
2 n n2 |
|
||||||||||||||||||||||||||
при n дроби |
n |
|
|
1 |
|
. Поэтому в качестве эталонного ряда вы- |
|||||||||||||||||||||
n2 |
n |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
бираем гармонический ряд, |
общий член которого vn |
|
|
1 |
. Воспользу- |
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
||
емся вторым признаком сравнения |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
li m |
un |
li m |
|
1 n |
|
: |
1 |
li m |
n(1 n) |
1 0 . |
||||||||||||||||
|
|
|
|
n n2 |
|
2 n n2 |
|||||||||||||||||||||
|
n v |
n 1 |
|
|
n |
n |
|
|
|
|
|||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как гармонический ряд |
|
1 |
|
расходится, то и исследуемый ряд |
|||||||||||||||||||||||
n |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
на основании теоремы 1.4.3 также расходится. |
||||||||||||||||||||||||||
2 n n2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 1.4.4 (признак Д Аламбера). Пусть дан ряд un с |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
положительными членами и существует предел |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
l i m |
un 1 |
l . |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
u |
n |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда 1) при l 1 ряд сходится;
2)при l 1 ряд расходится;
3)при l 1 вопрос о сходимости ряда остаётся открытым.
Доказательство. Пусть для некоторого ряда существует пре-
дел l i m |
un 1 |
l . Тогда из определения предела следует, что для лю- |
|
|
|||
n u |
n |
|
|
|
|
|
|
бого 0 , |
начиная с некоторого номера N0 , выполняются неравен- |
||
ства l un 1 l . un
18

1) Если l 1 , то найдётся такое 0 , для которого l 1 . Обо-
значим q l . Тогда из неравенства un 1 q n N0 следует, un
что
uN0 1 uN0 q ,
uN0 2 uN0 1q uN0 q2 ,
………………………………
uN0 k uN0 k 1q uN0 qk .
Так как ряд uN0 qk при | q | 1 сходится, то сходится ряд
k 1
|
|
|
|
|
|
|
|
|
|
|
uN0 k |
|
un , а следовательно, и ряд un . |
|
|
|
|||||
k 1 |
|
n N0 1 |
|
|
n 1 |
|
|
|
|
|
2) Если |
l |
1 , то найдётся |
такое 0 , для которого |
l q 1 . |
||||||
Тогда имеем неравенство |
un 1 |
q |
n N |
|
или |
u |
|
u q . Это |
||
|
0 |
|
||||||||
|
|
|
un |
|
|
n 1 |
n |
|||
|
|
|
|
|
|
|
|
|
||
означает, что, начиная с номера N0 , члены ряда возрастают. Поэтому необходимый признак сходимости не выполняется, и ряд расходится,
что и требовалось доказать. ■ Отметим, что признак Д Аламбера удобно применять, если об-
щий член ряда содержит показательные выражения и (или) факториалы.
Пример 1.4.7. Исследовать на сходимость ряд n .
n 1 2n
Решение. Имеем un |
n |
, un 1 |
|
n 1 |
. Найдём их отношение |
||
|
n |
n 1 |
|
||||
|
2 |
|
|
|
2 |
|
|
u |
1 |
|
n 1 |
|
|
n |
|
(n 1) 2n |
|
1 |
|
n 1 |
|
|
|
|
||||||||
n |
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
. Тогда |
|
|
|
|||||
u |
|
|
2n |
2n |
|
2n 1 n |
|
|
2 |
n |
|
|
|
|||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
l li m |
un 1 |
|
|
|
1 |
li m |
n 1 |
|
1 |
|
1 , следовательно, ряд сходится. |
|||||||||||||
u |
|
|
2 |
|
||||||||||||||||||||
|
n |
|
|
|
2 n |
|
n |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
Пример 1.4.8. Исследовать на сходимость ряд |
n |
|
. |
|||||||||||||||||||
|
|
n ! |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|

Решение. Имеем u |
|
|
|
nn |
, u |
|
|
|
|
|
|
(n 1)n 1 |
|
, |
|
|
|
|
|
|
|
|||||||||||||||||||
n |
|
n ! |
n 1 |
|
(n 1) ! |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
l li m |
u |
|
|
li m |
(n 1)n 1 n ! |
li m |
(n 1)n 1 n ! |
|
|
|
||||||||||||||||||||||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1) ! nn |
|
nn |
|
|
|
|
(n |
|
|
|
||||||||||||||||||||||||||
n |
u |
|
|
|
n |
|
(n |
|
n |
|
|
|
|
|
1) ! |
|
||||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
li m |
(n 1)n 1 |
n ! |
|
|
li m |
|
(n 1)n (n 1) |
|
|
n ! |
|
|
||||||||||||||||||||||||||||
|
nn |
|
|
|
(n 1) ! |
|
|
|
|
|
|
nn |
|
|
|
|
|
n !(n |
1) |
|||||||||||||||||||||
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
(n 1)n |
|
|
|
|
|
n 1 n |
|
|
|
|
|
|
|
|
1 n |
|
|
|
|
|
|
|
||||||||||||||||
li m |
|
|
|
|
|
li m |
|
|
|
|
|
|
li m 1 |
|
|
|
|
e 1 , |
|
|
|
|||||||||||||||||||
|
|
n |
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
следовательно, ряд расходится.
Теорема 1.4.5 (радикальный признак Коши). Пусть дан ряд
un
n 1
Тогда
|
|
|
с положительными членами, и существует предел li m n u l . |
||
n |
n |
|
|
|
|
1) при l 1 ряд сходится;
2)при l 1 ряд расходится;
3)при l 1 вопрос о сходимости ряда остаётся открытым.
|
|
Доказательство. |
Пусть для ряда un существует предел |
|
n 1 |
li m n u l . Тогда из определения предела следует, что для любого |
||||
n |
n |
|
|
|
|
|
|
|
|
0 найдётся такой номер N0 , что выполняются неравенства |
||||
|
l n u |
l , n N |
0 |
. |
|
n |
|
|
|
1). Если l 1 , то найдётся такое 0 , для которого l 1 . Обо-
значим q l . Тогда из неравенства |
|
|
q следует, что u |
|
qn |
|
n u |
n |
|||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n N0 . Так как ряд qn |
при | q | 1 |
сходится, то по признаку |
||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
сравнения (теорема 1.4.2) сходится и ряд un . |
|
|
||||
|
|
n 1 |
|
|
|
|
2). Если l 1 , то найдётся такое 0 , |
для которого l q 1 . |
||||||
|
|
|
|
qn |
|
|
|
Тогда из неравенства n u q получаем u |
n |
n N |
0 |
. Из расхо- |
|||
|
n |
|
|
|
|||
|
|
|
|
|
|
||
димости ряда qn при | q | 1 согласно признаку сравнения (теоре- |
|||||||
n 1
20

ма 1.4.2) следует расходимость ряда un , что и требовалось дока-
n 1
зать. ■ Признак Коши, как правило, используют, если общий член ис-
следуемого ряда имеет вид u |
(f (n)) (n) . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1.4.9. Исследовать на сходимость ряд |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3n 2 |
n |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7n 4 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
3n 2 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение. Имеем un |
|
|
|
|
|
|
|
|
|
, тогда |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
7n 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
3n |
|
2 n |
|
|
|
|
|
|
3n |
2 |
|
3 |
|
|
|
||||||||||||||
l li m n |
|
|
|
|
|
|
|
|
|
|
|
li m |
|
|
|
|
|
|
|
|
|
1 , |
||||||||||||
|
|
|
|
|
|
|
|
|
7n |
|
|
|
|
|
||||||||||||||||||||
|
|
n |
7n |
4 |
|
|
|
|
|
|
n |
4 |
|
7 |
|
|
|
|||||||||||||||||
следовательно, ряд сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Пример 1.4.10. Исследовать на сходимость ряд |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2n2 |
5 |
2n |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
2 |
1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2n2 5 |
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Решение. Имеем un |
|
|
|
|
|
|
|
|
|
|
|
|
|
, тогда |
|
|
|
|
|
|
|
|
|
|||||||||||
|
n |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2n2 5 |
2n |
|
|
|
|
|
|
|
|
|
2n2 5 |
2 |
|
2 |
2 |
|
||||||||||||||||
l li m n |
|
|
|
|
|
|
|
|
|
li m |
|
|
|
|
|
|
|
|
|
|
|
|
4 1 , |
|||||||||||
n |
2 |
1 |
|
|
n |
2 |
|
|
1 |
|
|
|||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
следовательно, ряд расходится.
§5. Знакочередующиеся ряды и их сходимость
Определение 1.5.1. Знакопеременным рядом называется ряд,
членами которого являются действительные числа произвольного знака.
Приведём примеры знакопеременных рядов:
si n si n 2 si n 3 |
si n n |
1 1 1 1 1 1 1 |
( 1)n(n 1) / 2 |
Частным случаем знакопеременных рядов являются знакочередующиеся ряды.
21

Определение 1.5.2. Знакопеременный ряд называется знакочередующимся, если его соседние члены имеют противоположные знаки.
Примеры знакочередующихся рядов:
1 2 3 4 |
( 1)n 1 n |
|
|
||||||||||
|
1 |
|
1 |
|
1 |
|
|
( 1)n 1 |
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
4 |
|
n |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
Рассмотрим знакопеременный ряд |
|
||||||||||
|
|
|
|
|
|
u1 u2 |
|
|
un |
|
(1.1) |
||
Некоторую информацию о сходимости этого ряда можно получить, рассматривая ряд, членами которого являются абсолютные величины (модули) членов знакопеременного ряда (1.1)
| u1 | | u2 |
| |
| un | , |
(1.2) |
который является рядом с положительными членами. Поэтому его сходимость можно изучать с помощью признаков, изложенных выше. Связь между сходимостью ряда (1.1) и сходимостью ряда (1.2) устанавливается следующей теоремой.
Теорема 1.5.1. Если ряд (1.2) сходится, то и ряд (1.1) также схо-
дится.
Доказательство. Пусть un есть знакопеременный ряд.
n 1
Составим ряд из модулей его членов | un |. По условию тео-
n 1
ремы ряд | un | сходится. Тогда по свойству 2 линейных операций
n 1
над рядами (см. §2) сходится ряд 2 | un |. Заметим, что для n
n 1
выполняются неравенства
0 un | un | 2 | un |.
Следовательно, по первому признаку сравнения (теорема 1.4.2) схо-
|
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
| u |
|
|
|
|
|
| u |
| можно представить в |
||||
дится ряд |
|
u |
|
|
| . |
А так как ряд |
|
|
||||||||
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
виде разности сходящихся рядов |
|
|
|
|
|
|||||||||||
|
|
n |
|
n |
n |
|
|
|
n |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
|
| u |
| |
u |
|
| u |
|
| |
|
| u |
|
| , то он сходится. ■ |
|||||
n 1 |
|
|
n 1 |
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|

Определение 1.5.3. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов.
Пример 1.5.1. Исследовать на сходимость ряд
1 |
1 |
|
1 |
|
1 |
|
|
( 1)n 1 |
|
|
2 |
4 |
8 |
2n |
|||||||
|
|
|
|
|
|
Решение. Данный ряд сходится на основании теоремы 1.5.1, так как сходится ряд, составленный из его модулей
|
|
|
1 |
1 |
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|||||||||||||||||
|
|
|
|
|
4 |
|
8 |
|
|
n |
|||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||
Действительно, этот ряд составлен из членов геометрической |
|||||||||||||||||||||||||||||||||
прогрессии со знаменателем q |
1 |
1 |
, поэтому он сходится. |
||||||||||||||||||||||||||||||
2 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 1.5.2. Исследовать на сходимость ряд |
|||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
( 1)n 1 |
|||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2 |
2 |
|
4 |
2 |
|
|
|
n |
2 |
|
||||||||||||||||||||||
|
|
2 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
( 1)n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. Ряд |
|
n2 |
|
|
сходится на основании теоремы 1.5.1, так |
||||||||||||||||||||||||||||
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
как сходится ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
, |
|||||||||||||||
|
|
2 |
|
2 |
|
|
2 |
|
2 |
||||||||||||||||||||||||
|
|
2 |
|
|
3 |
|
|
|
4 |
|
|
|
|
|
n |
|
|
|
|||||||||||||||
составленный из его модулей. Действительно, это обобщённый гармонический ряд, у которого p 2 1 .
Итак, ряды, приведённые в примерах 1.5.1 и 1.5.2, являются абсолютно сходящимися.
Определение 1.5.4. Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд, составленный из модулей его членов, расходится.
Для знакочередующихся рядов имеет место очень простой достаточный признак сходимости.
Теорема 1.5.2 |
|
(признак Лейбница). Если члены знакочере- |
|
|
|
дующегося ряда un |
удовлетворяют двум условиям: |
|
n 1 |
|
|
1) li m | un | 0 |
; |
|
n |
|
|
2) | u1 | | u2 | | u3 | 
то этот ряд сходится.
23

Доказательство. Пусть для знакочередующегося ряда un
n 1
выполняются оба условия теоремы. Заметим, что общий член знакочередующегося ряда можно всегда записать в виде un ( 1)n 1 an , где
an 0 .
Рассмотрим чётную частичную сумму ряда (с чётным числом членов)
s2n a1 a2 a3 a4 |
a2n 1 a2n |
(a1 a2 ) (a3 a4 ) |
(a2n 1 a2n ) . |
Из второго условия теоремы следует, что все выражения в круглых скобках неотрицательны. Следовательно, последовательность s2n является возрастающей при увеличении n . Докажем, что она ограни-
чена. Для этого представим s2n |
следующим образом: |
|
s2n a1 [(a2 a3 ) (a4 a5 ) |
(a2n 2 a2n 1 ) a2n ] . |
|
Отсюда следует, что s2n |
a1 для любого n , то есть возрас- |
|
тающая последовательность s2n |
ограничена сверху. Значит, она имеет |
|
предел li m s2n s . Покажем, |
что |
и последовательность частичных |
n |
|
|
сумм s2n 1 (нечётного числа слагаемых) тоже сходится к s . |
||
Для всех номеров n имеет место равенство s2n 1 s2n a2n 1 . |
||
Перейдём в этом равенстве к пределу при n и используем первое условие теоремы. Получаем
li m s2n 1 |
li m(s2n a2n 1 ) li m s2n |
li m a2n 1 s 0 s . |
|
||||||||
n |
n |
n |
|
n |
|
|
|
|
|||
Таким образом, |
последовательность частичных сумм |
sn схо- |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
дится к |
s . Это означает, что ряд |
un сходится. Что и требовалось |
|||||||||
|
|
|
|
n 1 |
|
|
|
|
|||
доказать. ■ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
( 1)n |
|
||
Пример 1.5.3. Исследовать на сходимость ряд |
n |
. |
|||||||||
n 1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
( 1)n |
|
|
|
|
||
Решение. О сходимости ряда |
|
n |
на основании достаточного |
||||||||
|
|
|
|
||||||||
n 1
признака сходимости 1.5.1 ничего сказать нельзя, так как ряд из моду-
24

|
|
|
|
( 1) |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
лей |
|
|
|
|
|
|
1 |
– гармонический ряд – расходится. Но для это- |
||||||||||||||||||||
n |
|
n |
||||||||||||||||||||||||||
n 1 |
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
го ряда выполняются оба условия теоремы Лейбница: |
|
|||||||||||||||||||||||||||
1) l i m |
1 |
|
0 |
; 2) |
1 |
|
|
|
1 |
, n . |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
n n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1)n |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||||||
Следовательно, |
ряд |
n 1 |
|
|
|
сходится. |
|
|
Отметим, |
что он сходится |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
условно, так как ряд из модулей |
|
|
( 1) |
|
|
|
|
1 |
расходится. |
|
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
n |
|
|
|
n 1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следствие 1.5.3. |
Для знакочередующегося ряда ( 1)n 1 an , |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
удовлетворяющего условиям теоремы Лейбница, |
остаток ряда |
rn |
||||||||||||||||||||||||||
можно оценить сверху по абсолютной величине | rn | an 1 . |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
знакочередующийся ряд |
( 1)n 1 an |
сходится, и |
его |
||||||||||||||||||||||||
n 1
сумма равна s . Тогда
s sn (an 1 an 2 an 3 ) .
Остаток ряда s sn rn , в свою очередь, является суммой знакочередующегося ряда и, следовательно, удовлетворяет условию | rn | an 1 (следствие 1.5.4). Таким образом, заменяя сумму ряда его
частичной суммой, получаем ошибку, абсолютная величина которой меньше абсолютной величины первого отброшенного члена ряда.
Поэтому следствие 1.5.4 используется в приближённых вычис-
|
|
( 1)n 1 |
|
|
лениях. Например, ряд |
|
сходится по признаку Лейб- |
||
(2n 1)3n 1 |
||||
|
|
|||
|
n 1 |
|
|
|
ница. Положим его сумму s приближённо равной сумме первых шести членов этого ряда, т.е.
6 |
( 1)n 1 |
|
|
|
|
|
|
|
s s6 |
|
|
|
|
0, 9068 . |
|
||
(2n 1)3 |
n |
1 |
|
|||||
n 1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
При этом получаем ошибку (погрешность), абсолютная величи- |
||||||||
|
|
|
1 |
1 |
|
|||
на которой меньше, чем a7 |
|
|
|
|
|
0, 0001 . |
||
13 36 |
9477 |
|||||||
25

Вопросы и задания для самопроверки
1. Для каждого из рядов запишите его un 1 член:
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
52n 1 |
|
|
|
||||||||||||
а) |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
б) |
|
|
. |
|
|
|
|
||||||||
|
3n (2n 1) |
|
|
|
|
|
|
|
n ! |
|
|
|
||||||||||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|||||
2. Найдите частичную сумму s3 для каждого ряда: |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а) |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
; |
|
|
|
|
|
|
|
|
|
|
|
б) n ! . |
|
|
|
|
|
|
|
|||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. Для некоторого ряда найдена его частичная сумма sn |
|
n |
|
. Схо- |
||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|||
дится ли этот ряд? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
4. Ряд |
cun сходится ( c const 0 ). Следует ли отсюда сходи- |
|||||||||||||||||||||||||||||
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
мость ряда un ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
5. Ряд un |
расходится. Верно ли, что li m un |
0 ? |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6. Ряд un |
сходится. Возможно ли равенство li m un 0, 5 |
? |
|
|
||||||||||||||||||||||||||
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
un |
|
|
|
|
|
||||
7. Сходится или расходится ряд un , |
если l i m |
2 ? |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
8. Верно ли утверждение: ряд |
|
|
|
|
|
|
|
сходится, |
|
так как |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
l n(n 1) |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|||
l i m |
|
|
|
1 |
|
|
0 ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n l n(n 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9. Можно ли сказать, что ряд |
|
|
|
|
расходится на основании того, |
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
n3n |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
что |
|
|
|
|
|
|
для n |
и ряд |
|
|
расходится? |
|
|
|
||||||||||||||||
n3n |
|
|
n |
|
n |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
26

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
10. Можно ли сказать, что ряд |
|
|
|
сходится на основании того, |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
n3n |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
что |
|
|
|
|
|
|
|
|
|
для n |
|
и ряд |
|
|
сходится? |
|
|
|
|
|
|
|
|
|||||||||||||||||
n3n |
|
3n |
|
|
3n |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
11. Среди следующих рядов укажите знакочередующиеся: |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
n |
|
|
cos n |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
а) |
|
cos |
|
|
; б) |
|
|
|
|
|
; в) |
( 1)n 1 2n ; г) |
|
t g |
|
|
|
. |
||||||||||||||||||||||
n2 |
|
3 |
|
n2 |
n |
6n |
||||||||||||||||||||||||||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
n 1 |
|
|
|
|
n 1 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
12. Укажите ряды, к которым применим признак Лейбница: |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
( 1)n 1 |
|
|
|
|
cos n |
|
|
|
( 1)n (n 1) |
|||||||||||||||||||||
а) |
|
|
|
|
; б) |
|
|
|
; в) |
|
|
; г) |
|
|
. |
|||||||||||||||||||||||||
n3 |
4 |
|
n4 |
|
l n(n 4) |
|
2n 1 |
|||||||||||||||||||||||||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
13. Сходится ли ряд ( 1)n 1 an , если l i m un |
|
? |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
n |
|
6 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
14. Известно, что для членов ряда |
un |
( un |
0 ) имеет место нера- |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
венство |
l i m |
un 1 |
1 . Что можно |
|
|
сказать о |
сходимости |
интеграла |
||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
u |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
u(x)dx ?
1
27
