Скалярное, векторное и смешанное

произведения векторов

16. Найти координаты единичного вектора (орта) , сонаправленного с вектором =(-2,3,5).

17. Два вектора =(-2,3,6) и =(7,–4,-4) приложены к одной точке. Найти координаты:

а) ортов и векторов и ;

б) вектора +;

в) вектора , направленного по биссектрисе угла между векторами и при условии, что .

18. Найти проекцию вектора =(2,1,0) на направление вектора =.

19. Найти проекцию вектора =(,-1,7) на ось, составляющую с координатными осями Ох и Оz углы , а с осью Оу – острый угол β.

20. В четырехугольнике ОABC при вершине О имеет величену , а диогональ ОВ является биссектрисой этого угла. Известно, что Найти величину угла между векторами и , используя последовательность действий:

а) ввести декартову прямоугольную систему координат в точке О так, чтобы ось Ох была направлена по стороне ОС четырехугльника (в связи с этим сторону ОС желательно расположить на рисунке горизонтально);

б) найти в этой системе координаты точек О,А, В, С,

в) найти координаты векторов и

г) найти по формуле ;

д) подсчитать искомый угол по формуле .

21. В плоскости XOY найти вектор , перпендикулярный вектору и имеющий одинаковую с ним длину.

22. На векторах и постоен треугольник. Найти длину медианы, провеенной из вершины А, если .

23. Вычислить координаты векторного произведения и его длину , если =(0,1,2), .

24. Даны вершины треугольника АВС:: А(3,-1,4), В(5,2,3) и С(-1,4,0). Найти площадь треугольника и длину высоты, опущенной из вершины А.

25. Вычислить , , , .

26. Найти вектор ортогонален векторам = и если где

27. Вычислить смешанное произведение векторов , , .

28. Установить, компланарны ли векторы , , .

29. Вычислить объем пирамиды, вершины которой А(1,2,3), В(9,6,4), С(3,0,4), D(5,2,6).

30. Вектор перпендикулярен к векторам и ; Зная, что, , , , найти , если тройка векторов - правая.

4. Аналитическая геометрия в пространстве:

плоскость и прямая в пространстве;

Поверхности второго порядка

31. Составить уравнение плоскости, проходящей через точку А(3;1;2), параллельную плоскости .

32. Составить уравнение плоскости, проходящей через две паралельные прямые: .

33. Составить уравнение плоскости, проходящей через прямую перпендикулярно плоскости .

34. Составить уравнение плоскости, которая проходит через точку А(1;0;1) перпендикулярно двум плоскостям: , .

35. Найти расстояние от точки М(-1;4;5) до плоскости

36. Найти оси Ох, найти координаты точек, отстоящих от плоскости 3x+4z-3=0 на расстоянии d=3.

37. Даны вершины треугольника А (-1,4,1), В (1,3,3), С (5,-1,10). Составить канонические уравнения биссектрисы его внутренго угла при вершине В.

38. Составить канонические уравнения прямой, проходящей через точку М(0;1;2), параллельно прямой , , .

39. Найти координаты точки пересечения прямой и плоскости .

40. Найти проекцию точки М (1;-4;3) на прямую x=t+2, y=-2t+4, z=5t.

41. Найти координаты точки М₁, симметричной точке М₂₍2,3,4) относительно плоскости 2х-у+2z=0.

42. Найти координаты точки М₁, симметричной точке М₂(3, 2,5) относительно прямой .

43. Вычислить расстояние от точки М(3;0;1) от прямой .

44. Составить кононические уравнение прямой которая проходит через точку M₀(4,-1,-3) перпендикулярно плоскости П: 3х-2у-3z-5=0 и пересекает прямую l: используя последовательность действий:

а) найти все уравнение плоскости П₁, проходящее через точку М₀ паралельно плоскости П(см. задачу 31);

б) найти координаты точки М₁ пересечения прямой l и плоскости П₁ (см. задачу 39);

в) найти коанические уравнения искомой прямй как прямой, проходящей через точки М₀ и М₁.

45. Даны координаты вершины пирамиды А₁(5, 4, 0), А₂(4, 3, 0), А₃(1, 0, -1), А₄(2, 4, 7).

Найти: 1) угол между ребрами А₁А₂ и А₁А₄;

2) угол между ребром А₁А₄ и гранью А₁А₂А₃;

3) уравнение прямой А₁А₂;

4) уравнение плоскости А₁А₂А₃;

5) уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃.

46. Построить эскиз тела, ограниченного поверхностями:

а) х²-у²+z²=0; у=2-х²-z²; (у≥0),

б) z=1-y²; x+y=1; x=0; y=0; z=0 (у≥0)

5. Элементы линейной алгебры: системы линейных

уравнений; МАТРИЦЫ; линейное векторное

пространство; линейные операторы;

47. Решить систему линейных уравнений методом Гаусса

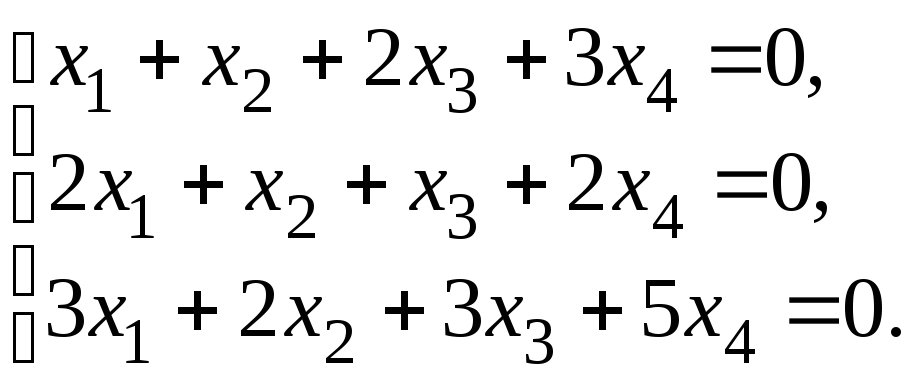
48. Найти все вещественные матрицы, перестановочные с матрицей .

49. Найти матрицу , где

А=, В= , С= .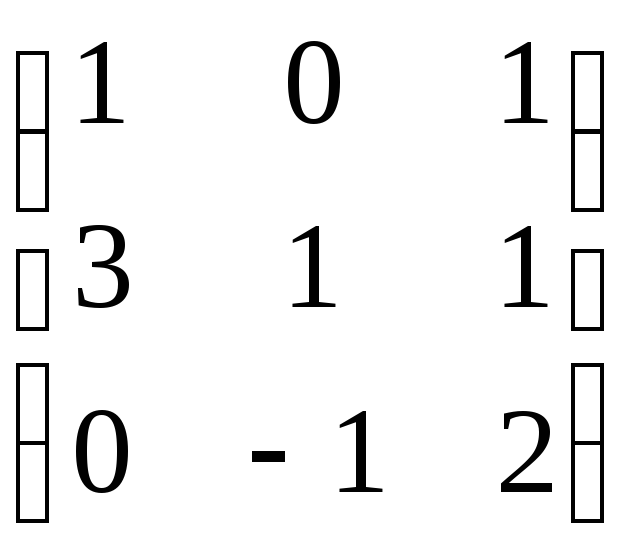

50. Найти ранги матриц:

а) ; б) .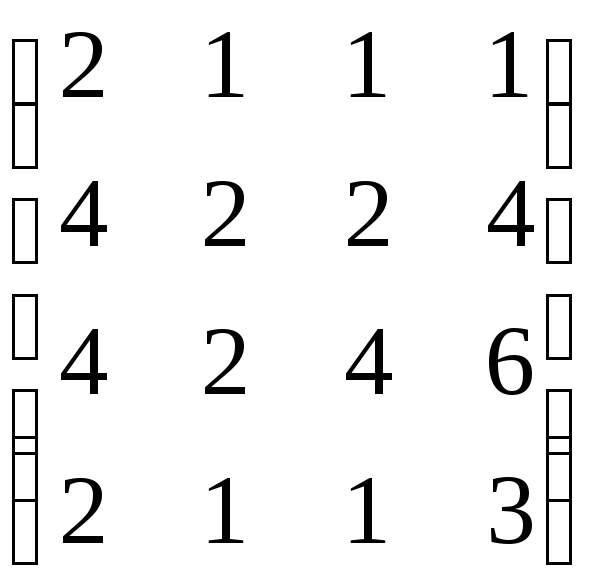

51. Дана система линейных уравнений

Доказать ее совместность и решить тремя способами:

а) методом Гаусса;

б) средствами матричного исчисления;

в) по формулам Крамера.

52. Являются ли вещественными линейным пространствами:

а) все векторы (х,у,z) арифметического пространства R₃ координаты которых удовлетворяют уравнению 2х-у+3z=0;

б) все векторы (х,у,z) из R ₃ координаты которых удовлетворяют уравнению : 2х-у+3z=1.

53. Найти все значения , при которых вектор линейно выражается через векторы , если =(2,2, ), =(1,4,5), =(3,1,4),

=(-1,-1, -2).

54. Выяснить, является ли данная система векторов из линейно зависимой? =(2,1,0,–1), =(1,2,2,–2), =(1,1,-2,-2), =(3,2,-2,-3).

55. Выяснить геометрический смысл действия линейных операторов, данных в пространстве R₃, матрицы которых относительно некоторого прямоугольного базиса имеют вид

а) ; б)

.56. Показать, что дефференцирование является линейным преобразованием пространства всех многочленов степени 3 от одного неизвестного с вещественными коэффициентами и найти матрицу этого преобразования в базисе:

f₁(x)=1, f₂(x)=x, f₃(x)=x², f₄(x)=x³.

57. Линейный оператор - оператор зеркального отражения векторов плоскости относительно прямой у=-2х, а оператор - оператор повтора плоскости вокруг начала координат на угол. Найти матрицы операторов ; и в базисе .

58. Найти собственные значения и собственные векторы линейного преобразования, заданного в некотором базисе матрицей .