
ВАРИАНТ №15
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ: ПРОСТЕЙШИЕ ЗАДАЧИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ; ПРЯМАЯ НА ПЛОСКОСТИ; ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ
1. Даны вершины треугольника А(2, 4), В(–1, 2), С(3, 5). Составить уравнения его высот.
2. Даны уравнения двух сторон прямоугольника х–2у+7=0, х–2у+22=0 и уравнения одной из его диагоналей 7х+у–11=0. Найти координаты точек пересечения диагонали с этими сторонами и уравнения двух других сторон прямоугольника.
3. Написать уравнения
сторон квадрата, диагонали которого
служат осями координат. Длина сторон
квадрата равна
![]() .
.
4. Даны последовательно вершины выпуклого четырехугольника
А(–2, –1), В(4, 7), С(8, 4), D(–1, –8). Определить уравнения его диагоналей и координаты точки пересечения его диагоналей.
5. Отрезок, ограниченный точками А(8, 2) и В(11, 8), разделен на три равные части. Определить координаты точек деления.
6. Даны середины сторон треугольника: М1(–2, 7), М2(1, 9), М3(–1, 2). Составить уравнения его сторон.
7. Найти расстояние от точки А(–3, 4) до прямой, проходящей через точки М1(–4, 6) и М2(–2, 9).
8. Точка А(–1, 2) является вершиной квадрата, одна из сторон которого лежит на прямой х–2у+10=0. Найти площадь квадрата.
9. Установить, какие линии определяются в полярных координатах следующими уравнениями (построить их на чертеже):
а)
![]() б)
б)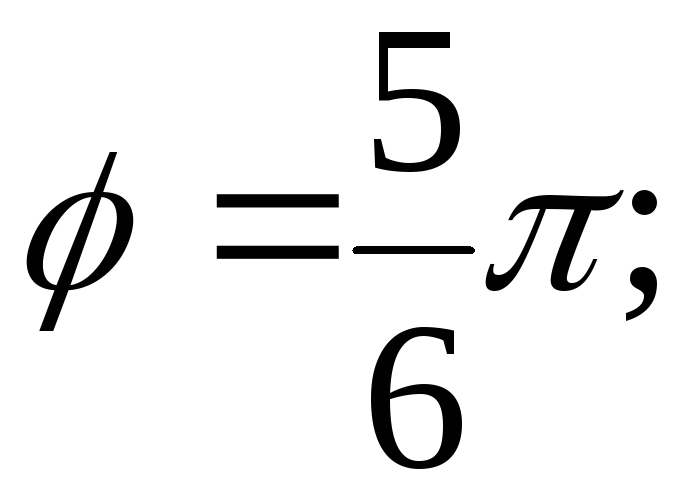 в)
в)![]() г)
г)![]() д)
д)![]()
е)
![]()
10. Установить,
какая линия определяется уравнением
![]() .
Найти координаты ее центра, полуоси,
эксцентриситет. Сделать чертеж.
.
Найти координаты ее центра, полуоси,
эксцентриситет. Сделать чертеж.
11. Составить
уравнение гиперболы, зная, что расстояние
между ее вершинами равно 24 и фокусы суть
![]() .
.
12. Составить уравнение линии, каждая точка которой находится вдвое дальше от точки А(6, 5), чем от оси ординат. Определить, какая это линия; сделать чертеж.
13 Линия задана
уравнением
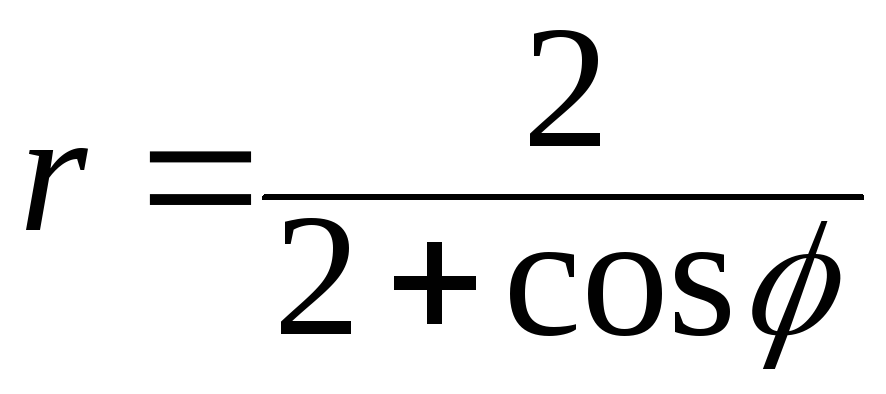 в полярной системе координат. Требуется:
а) построить линию по точкам, начиная
от
в полярной системе координат. Требуется:
а) построить линию по точкам, начиная
от![]() до
до![]() и придавая
и придавая![]() значения через промежуток
значения через промежуток![]() ;
б) найти уравнение данной линии в
декартовой прямоугольной системе
координат, у которой начало совпадает
с полюсом, а положительная полуось
абсцисс – с полярной осью; в) по полученному
уравнению определить, какая это линия.
;
б) найти уравнение данной линии в
декартовой прямоугольной системе
координат, у которой начало совпадает
с полюсом, а положительная полуось
абсцисс – с полярной осью; в) по полученному
уравнению определить, какая это линия.
2. Определители, базис в пространстве, координаты вектора
14. Вычислить определители:
а) по правилу треугольника;
б) разложением по элементам первой строки;
в) разложением по элементам второго столбца;
г) сведением к треугольному виду:
а)
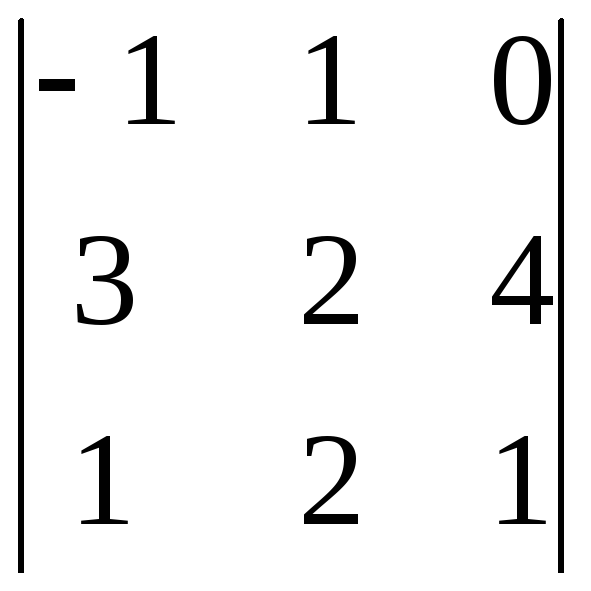 ,
б)
,
б) ,
в)
,
в) ,
г)
,
г)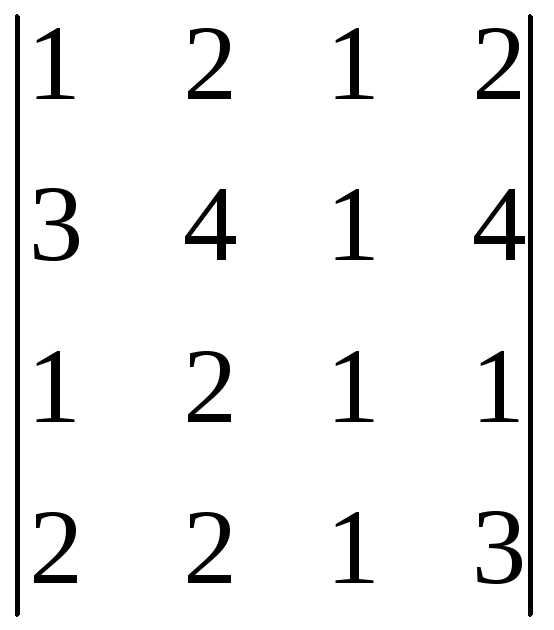 .
.
15.
Даны векторы:
![]() 1=(2,
–1,
3);
1=(2,
–1,
3);
![]() 2=(5,
0, –2);
2=(5,
0, –2);
![]() 3=(–2,
1, –1);
3=(–2,
1, –1);
![]() =(–7,
1, 5) в некотором базисе. Показать, что
первые три вектора сами образуют базис
и найти координаты вектора
=(–7,
1, 5) в некотором базисе. Показать, что
первые три вектора сами образуют базис
и найти координаты вектора
![]() в этом базисе.
в этом базисе.
3. Линейные операции над векторами. Проекция вектора на ось. Скалярное, векторное и смешанное произведения векторов.
16. Найти координаты
единичного вектора (орта)
![]() ,
сонаправленного с вектором
,
сонаправленного с вектором
![]() =(–3,
2, –2).
=(–3,
2, –2).
17. Два вектора
![]() =(7,
–6, –6) и
=(7,
–6, –6) и
![]() =(–4,
7, 4) приложены
к одной точке. Найти координаты:
=(–4,
7, 4) приложены
к одной точке. Найти координаты:
а) ортов
![]() и
и![]() векторов
векторов![]() и
и![]() ;
;
б) вектора
![]() +
+![]() ;
;
в) вектора
![]() ,
направленного по биссектрисе угла между
векторами
,
направленного по биссектрисе угла между
векторами![]() и
и![]() при условии, что
при условии, что![]() .
.
18. Найти проекцию
вектора
![]() на направление вектора
на направление вектора
![]() =(–3,
0, 4).
=(–3,
0, 4).
19. Найти проекцию
вектора
![]() на ось, составляющую с координатными
осями
на ось, составляющую с координатными
осями![]() и
и![]() углы
углы![]() ,
,![]() ,
а с осью
,
а с осью![]() тупой угол
тупой угол![]() .
.
20. В равнобедренном
треугольнике OAB
(![]() )точка C
делит сторону AB
в отношении 1:4
(считая от вершины A).
Найти угол между векторами
)точка C
делит сторону AB
в отношении 1:4
(считая от вершины A).
Найти угол между векторами
![]() и
и![]() ,
если
,
если![]() =60.
=60.
Указание. Использовать последовательность действий:
А) ввести декартову прямоугольную систему координат с началом в точкеО так, чтобы ось была направлена по основанию ов треугольника;
б) найти в этой
системе координаты векторов
![]() и
и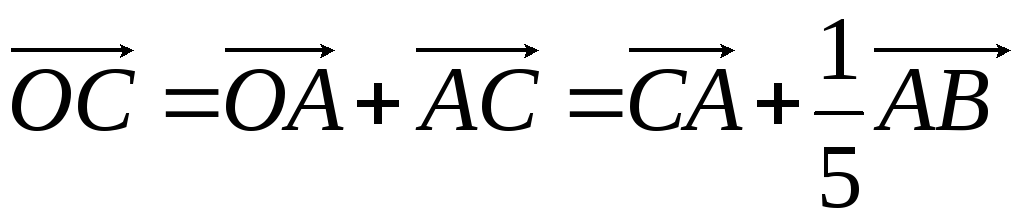 ;
;
в) подсчитать
величину искомого угла по формуле
![]()
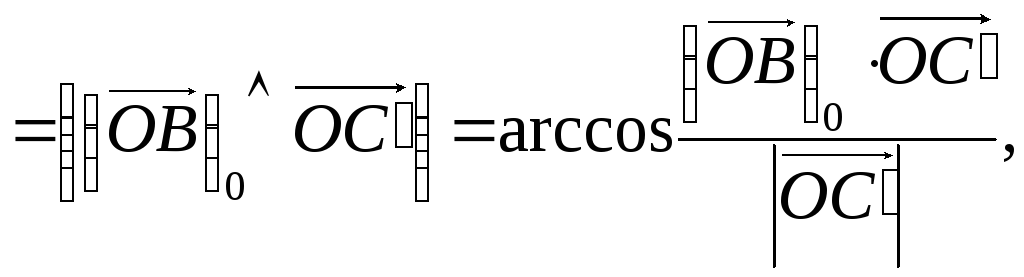
где
![]() -
орт вектора
-
орт вектора![]() ,
,![]() =
=![]() .
.
21. В прямоугольном
треугольнике ABC
(![]() ),
),![]() ,
,![]() .
Найти
.
Найти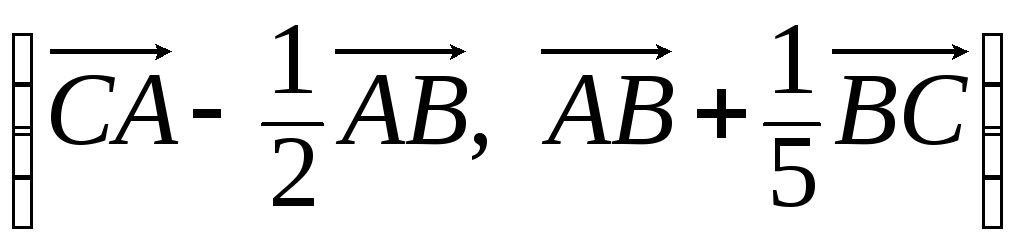 .
.
22. Дано
![]() ,
,![]() ,
,![]() ,
,![]() .
Найти
.
Найти![]() и
и![]() .
.
23. Найти координаты
векторного произведения
![]() и его длину
и его длину![]() ,
если
,
если
![]() =(4,
–3, 4),
=(4,
–3, 4),
![]() .
.
24. Даны вершины треугольника А(6, –2, –2), В(8, –4, –5), С(10, –2, 4). Найти площадь треугольника и длину его высоты, опущенной из вершины В.
25. Найти координаты
вектора
![]() ,
перпендикулярного векторам
,
перпендикулярного векторам![]() и
и![]() ,
если
,
если![]() и вектор
и вектор![]() составляет с осью
составляет с осью![]() тупой угол.
тупой угол.
26. Вычислить
![]() ,
если
,
если![]() ,
,![]() ,
,![]() .
.
27. Вычислить
смешанное произведение векторов
![]() ,
,![]() ,
,![]() .
.
28. В правом базисе
![]() заданы векторы:
заданы векторы:![]() ,
,
![]() ,
,
![]() .
Показать, что эти векторы не компланарны,
установить ориентацию тройки
.
Показать, что эти векторы не компланарны,
установить ориентацию тройки![]() .
.
29. Вычислить объем пирамиды, вершины которой А(–1, 10, –1), В(3, 4, 3), С(3, 9, 1), D(2, 12, 6).
30. Вектор
![]() перпендикулярен к векторам
перпендикулярен к векторам![]() и
и![]() .
Вычислить
.
Вычислить![]() ,
если
,
если![]() ,
,![]() ,
,![]() ,
,![]() ,
а тройка векторов
,
а тройка векторов![]() – правая.
– правая.
4. Аналитическая геометрия в пространстве: плоскость и прямая в пространстве; поверхности второго порядка
31.
Составить
уравнение плоскости, проходящей через
точку
![]() ,
параллельную плоскости
,
параллельную плоскости![]() .
.
32. Составить
уравнение плоскости, проходящей через
точку
![]() и прямую
и прямую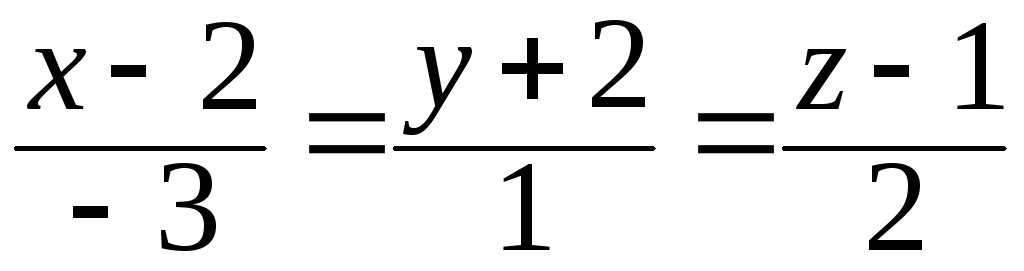 .
.
33. Составить
уравнение плоскости, проходящей через
прямую
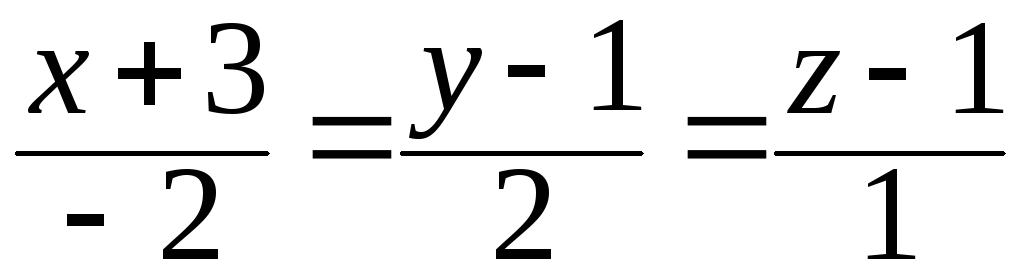 ,
перпендикулярно плоскости
,
перпендикулярно плоскости![]() .
.
34. Составить
уравнение плоскости, которая проходит
через точку
![]() перпендикулярно двум плоскостям:
перпендикулярно двум плоскостям:![]() ,
,![]() .
.
35. Найти расстояние
![]() от точки
от точки![]() до плоскости
до плоскости![]() .
.
36. Найти параметрические
уравнения прямой, заданной как линия
пересечения двух плоскостей
![]() и
и![]() .
.
37. Даны вершины треугольника А(–1, 5, –3), В(2, 5, 1), С(1, 6, –1). Составить канонические уравнения биссектрисы его внутреннего угла при вершине А.
38. Составить
канонические уравнения прямой, проходящей
через точку
![]() ,
параллельной прямой
,
параллельной прямой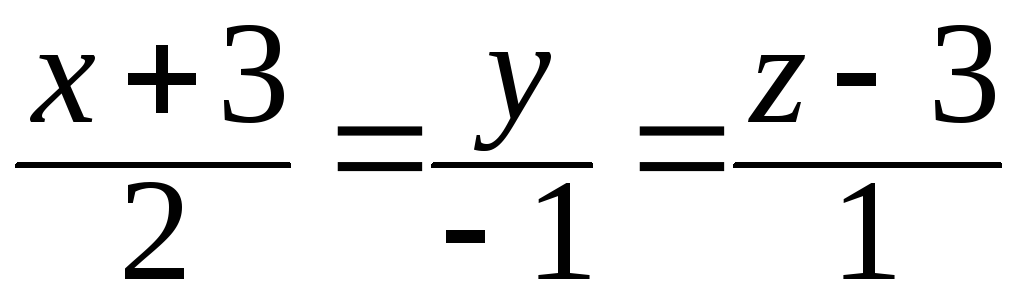 .
.
39. Найти координаты
точки пересечения прямой
![]()
![]()
![]() и плоскости
и плоскости![]() .
.
40. Найти проекцию
точки
![]() на прямую
на прямую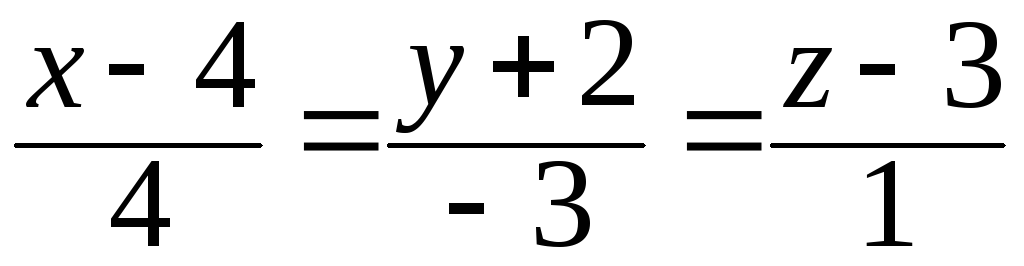 .
.
41. Найти координаты
точки
![]() ,
симметричной точке
,
симметричной точке![]() относительно плоскости
относительно плоскости![]() .
.
42. Найти координаты
точки
![]() ,
симметричной точке
,
симметричной точке![]() относительно прямой
относительно прямой .
.
43. Вычислить
расстояние
![]() от точки
от точки![]() до прямой
до прямой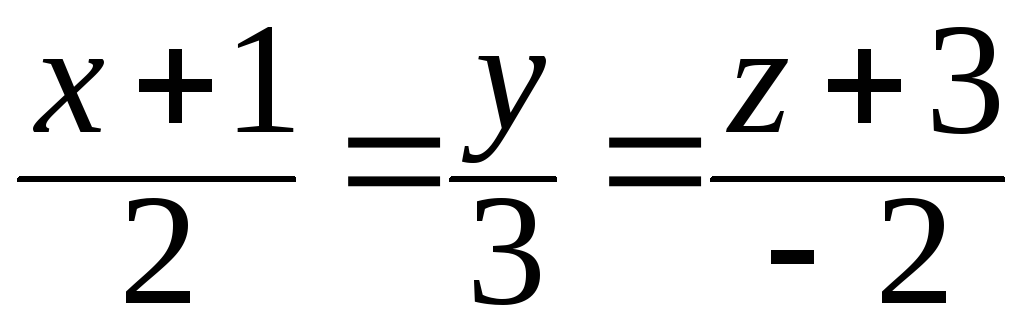 .
.
44. Составить
канонические уравнения прямой
![]() ,
которая проходит через точку
,
которая проходит через точку![]() и пересекает прямые
и пересекает прямые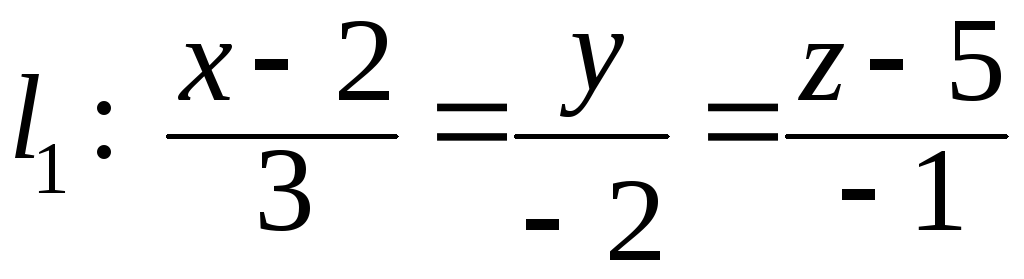 и
и .
.
Указание. Использовать последовательность действий:
а) найти координаты
нормального вектора
![]() к плоскости
к плоскости![]() ,
проходящей через точку
,
проходящей через точку![]() и прямую
и прямую![]() ,
взяв векторное произведение
,
взяв векторное произведение![]() ,
где
,
где
![]() (3,
–2, –1) –
направляющий вектор прямой
(3,
–2, –1) –
направляющий вектор прямой
![]() ,
,![]() – точка прямой
– точка прямой![]() (см. задачу №32);
(см. задачу №32);
б) аналогично найти
координаты нормального вектора
![]() к плоскости
к плоскости![]() ,
проходящей через точку
,
проходящей через точку![]() и прямую
и прямую![]() ,
взяв векторное произведение
,
взяв векторное произведение![]() ,
где
,
где
![]() (2,
3, –5) –
направляющий вектор прямой
(2,
3, –5) –
направляющий вектор прямой
![]() ,
,![]() – точка прямой
– точка прямой![]() ;
;
в) найти координаты
направляющего вектора
![]() искомой прямой
искомой прямой![]() ,
взяв векторное произведение
,
взяв векторное произведение![]() .
.
г) составить
канонические уравнения искомой прямой
![]() ,
проходящей через точку
,
проходящей через точку![]() в направлении вектора
в направлении вектора![]() .
.
45. Даны координаты вершины пирамиды А1(4, 5, 5), А2(3, 5, 4), А3(2, 3, 6), А4(3, 1, 9). Найти: 1) угол между ребрами А1А2 и А1А4; 2) угол между ребром А1А4 и гранью А1А2А3; 3) уравнение прямой А1А2; 4) уравнение плоскости А1А2А3; 5) уравнение высоты, опущенной из вершины А4 на грань А1А2А3.
46. Построить эскиз тела, ограниченного поверхностями:
а)
![]() ,
,![]() ,
,![]() ;
;
б)
![]() ,
,![]() ,
,![]() ;
;
5. Элементы линейной алгебры: системы линейных уравнений; матрицы; линейное векторное пространство; линейные оиператоры
47. Решить систему линейных уравнений методом Гаусса
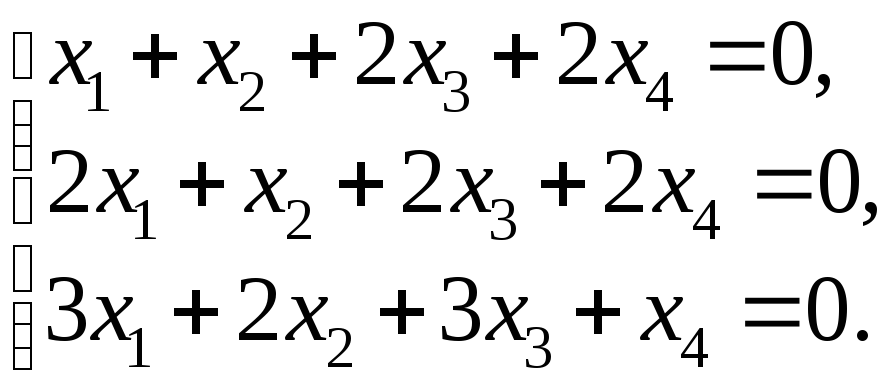
48. Найти все
вещественные матрицы, перестановочные
с матрицей
![]() .
.
49. Найти матрицу
![]() ,
где
,
где
А= ,
В=
,
В= ,
С=
,
С= .
.
50. Найти ранг матриц:
а)
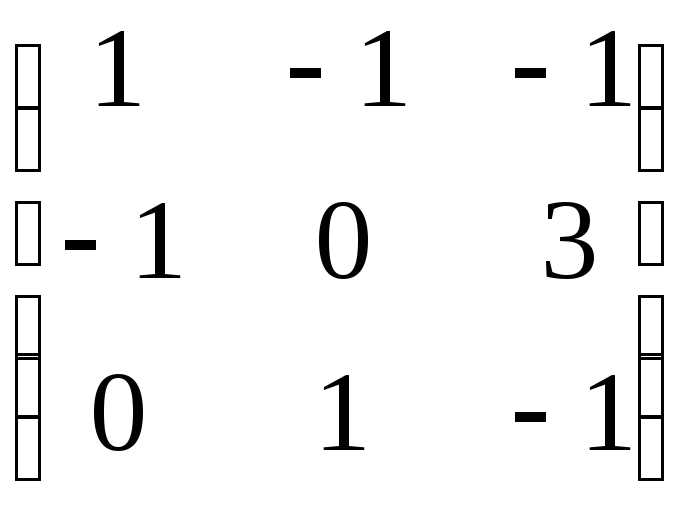 ;
б)
;
б)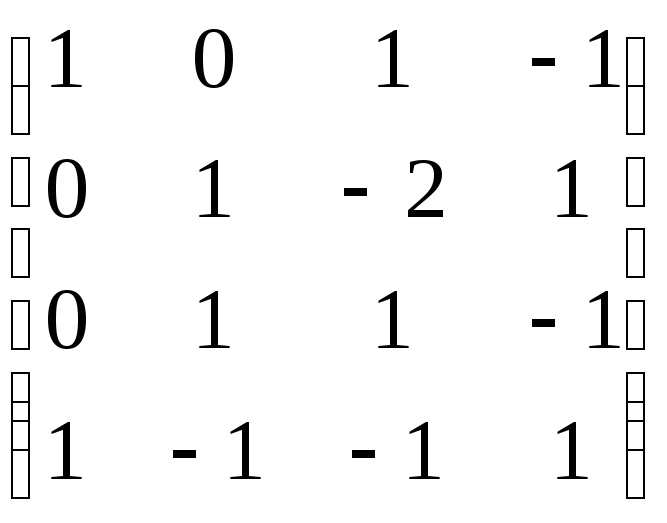 .
.
51. Дана система линейных уравнений
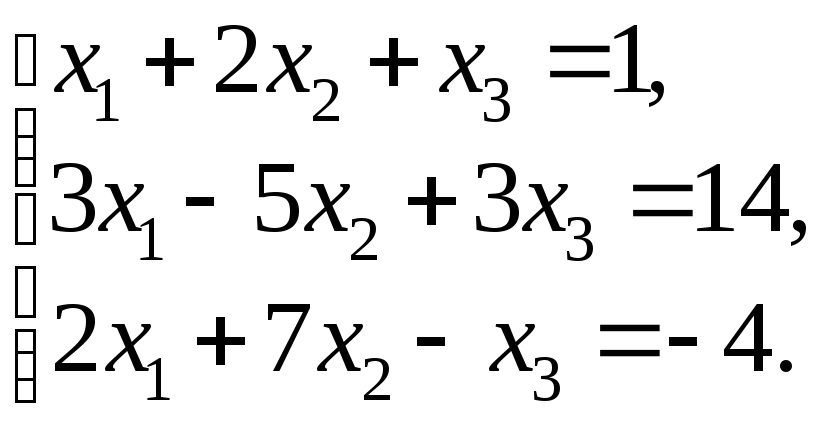
Доказать ее совместность и решить тремя способами: а) методом Гаусса; б) средствами матричного исчисления; в) по формулам Крамера.
52. Будет ли вещественным линейным пространством:
а) множество всех
вещественных матриц 2-го порядка вида
![]() ;
;
б) множество всех
вещественных матриц 2-го порядка вида
![]() .
.
53. Найти все значения
![]() ,
при которых вектор
,
при которых вектор![]() линейно выражается через векторы
линейно выражается через векторы![]() ,
если
,
если
![]() =(4,
3,
=(4,
3,![]() ),
),![]() =(2,
4, 6),
=(2,
4, 6),![]() =(3,
1, 4),
=(3,
1, 4),![]() =(2,
1, 3).
=(2,
1, 3).
54. Выяснить, является
ли данная система векторов из
![]() линейно зависимой?
линейно зависимой?
![]() =(1,
3, 1, 3),
=(1,
3, 1, 3),![]() =(2,
0, 1, 2),
=(2,
0, 1, 2),![]() =(4,
1, 0, 0),
=(4,
1, 0, 0),![]() =(5,
4, 1, 3).
=(5,
4, 1, 3).
55. Выяснить
геометрический смысл действия линейных
операторов, данных в пространстве
![]() ,
матрицы которых относительно некоторого
прямоугольного базиса имеют вид:
,
матрицы которых относительно некоторого
прямоугольного базиса имеют вид:
а)
 ;
б)
;
б)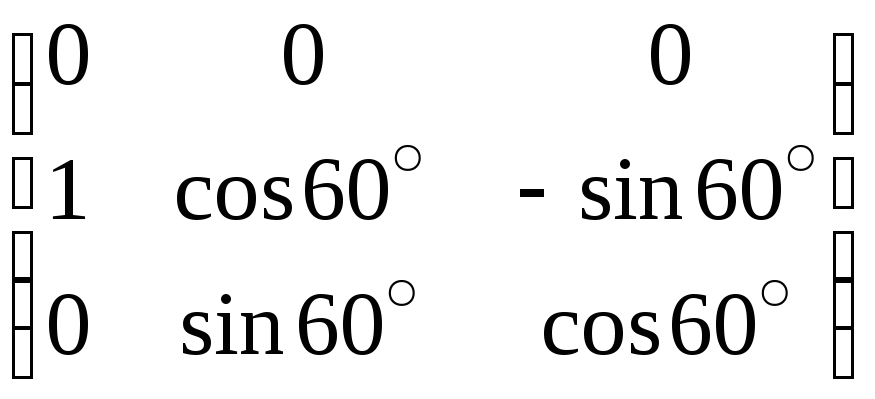 .
.
56. В пространстве
задан оператор
![]() так:
так:![]() ,
где
,
где![]() ,
,![]() .
Проверить линейность оператора
.
Проверить линейность оператора![]() и найти его матрицу в базисе
и найти его матрицу в базисе![]() .
.
57. В пространстве
![]() линейный оператор
линейный оператор![]() зеркально отражает векторы относительно
прямой
зеркально отражает векторы относительно
прямой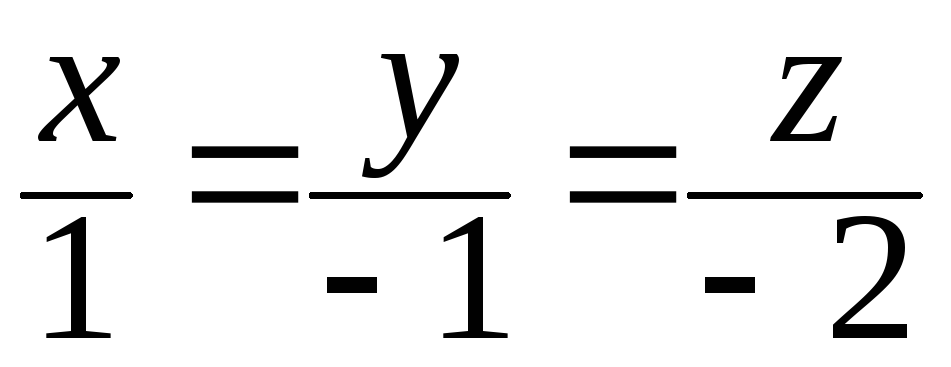 ,
а линейный оператор
,
а линейный оператор![]() ортогонально проецирует векторы на
плоскость
ортогонально проецирует векторы на
плоскость![]() .
Найти матрицу оператора
.
Найти матрицу оператора![]() в базисе
в базисе![]() .
.
58. Найти собственные
значения и собственные векторы линейного
преобразования, заданного в некотором
базисе матрицей
 .
.
