
Ответы:
1. а)
![]() ,
б)
,
б)![]() ,
в)
,
в)![]() или
или
 .
2.катет
–
.
2.катет
–
![]() ,гипотенуза
,гипотенуза
![]() или
или
![]() .
.
3.
![]() ,
,![]() ,
,![]() .
4.
.
4.![]() .
5. (–2, –5), (0, –3). 6.
.
5. (–2, –5), (0, –3). 6.![]() .
7. 1)
.
7. 1)![]() ,
,![]() ,
,![]() ,
,![]() 2)
2)![]() ,
,![]() ,
,![]() ,
,![]() .
8.
.
8.![]() ,
,![]() ,
,![]() .
9. 1)окружность
с центром в полюсе и радиусом 16. 2) луч,
выходящий из полюса, наклоненный к
полярной оси под углом
.
9. 1)окружность
с центром в полюсе и радиусом 16. 2) луч,
выходящий из полюса, наклоненный к
полярной оси под углом
![]() .
3)прямая,
перпендикулярная к полярной оси,
отсекающая на ней считая, от полюса,
отрезок
.
3)прямая,
перпендикулярная к полярной оси,
отсекающая на ней считая, от полюса,
отрезок
![]() .
4)прямая,
расположенная в верхней полуплоскости,
параллельная полярной оси, отстоящая
от нее на расстоянии равном
12. 5) окружность
с центром
.
4)прямая,
расположенная в верхней полуплоскости,
параллельная полярной оси, отстоящая
от нее на расстоянии равном
12. 5) окружность
с центром
![]() и радиусом4.
6) окружность
с центром
и радиусом4.
6) окружность
с центром
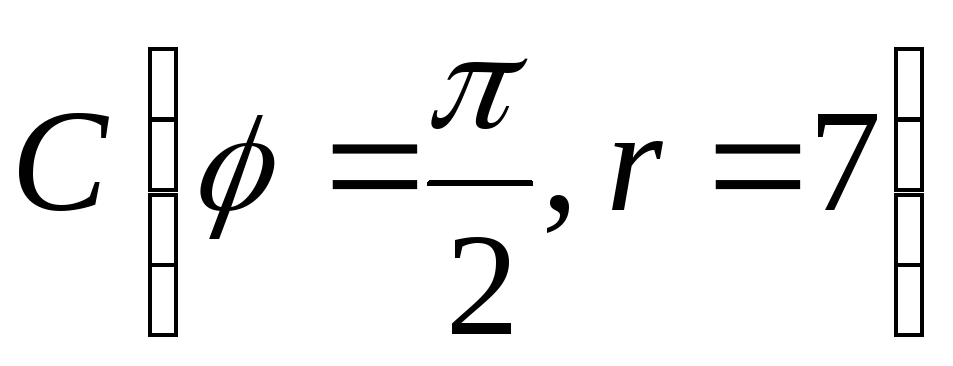 и радиусом7.
10. гипербола
и радиусом7.
10. гипербола
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,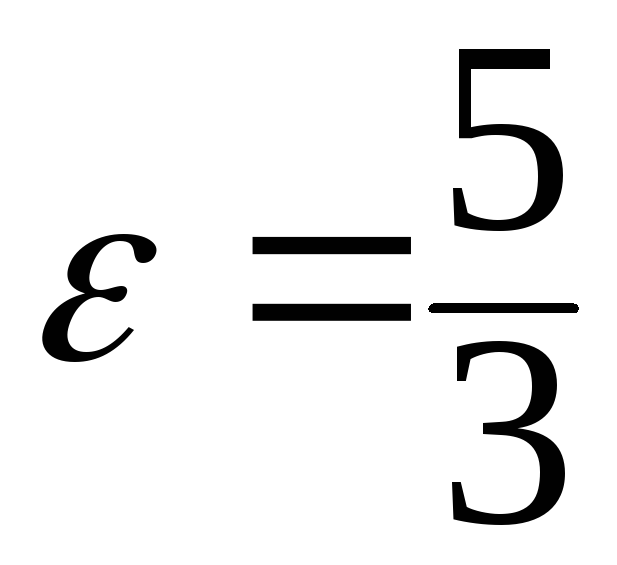 .
.
11. ![]() .
.![]() ,
,
![]() ,
,![]() ,
,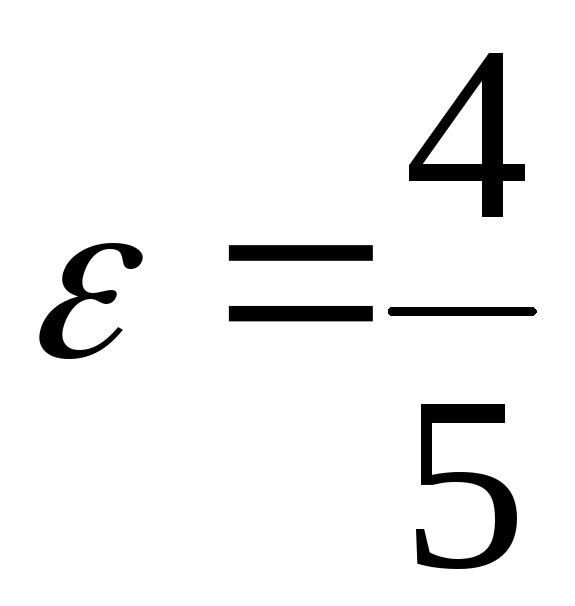
12. ![]() . 13. нижняя
ветвь сопряженной гиперболы:
б) в)
. 13. нижняя
ветвь сопряженной гиперболы:
б) в)  .
14. а) –22, б) 15, в) –7, г) –2. 15.
.
14. а) –22, б) 15, в) –7, г) –2. 15.
![]() .
.
16.
![]() .
17.
.
17.![]() ,
,![]() ,
,![]() ,
,![]() .
18. 4. 19. 6.
.
18. 4. 19. 6.
20.
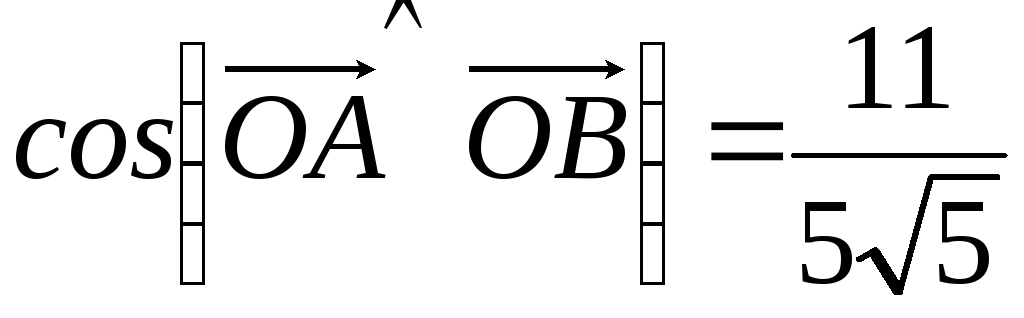 .
21.
.
21.![]() .
22.
.
22. .
.
23.
![]() ,
,![]() .
24.
.
24.![]() кв. ед.,
кв. ед.,![]() .
.
25.
![]() .
26.
.
26.![]() .
27. -10. 28.точки
лежат в одной плоскости.
29.
.
27. -10. 28.точки
лежат в одной плоскости.
29.
![]() куб. ед.
30. 18. 31.
куб. ед.
30. 18. 31.
![]() .
.
32.
![]() .
33.
.
33.![]() .
34.
.
34.![]() .
35.
.
35.![]() .
36.
.
36.![]() .
37.
.
37.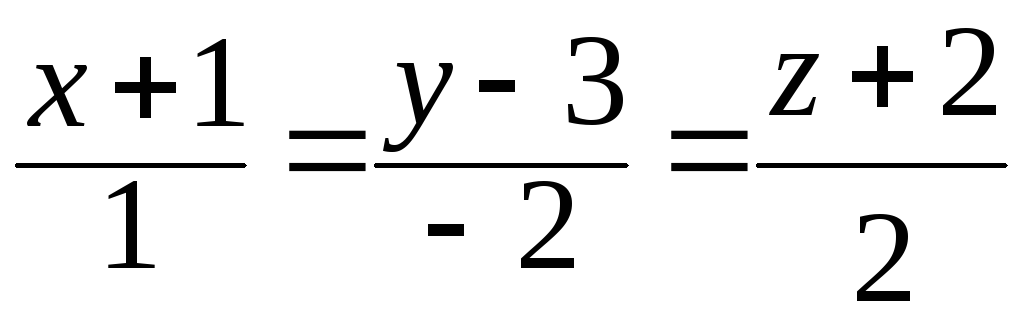 .
.
38.
![]() ,
,![]() ,
,![]() .39.
.39.
![]() .
40.
.
40. .
41.
.
41.![]() .
42.
.
42.![]() .
43.
.
43.![]() .
44.
.
44.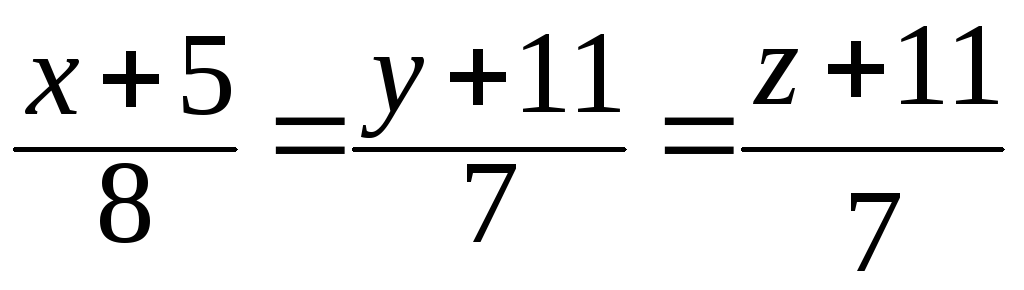 .
.
45. 1)
 ,
2)
,
2)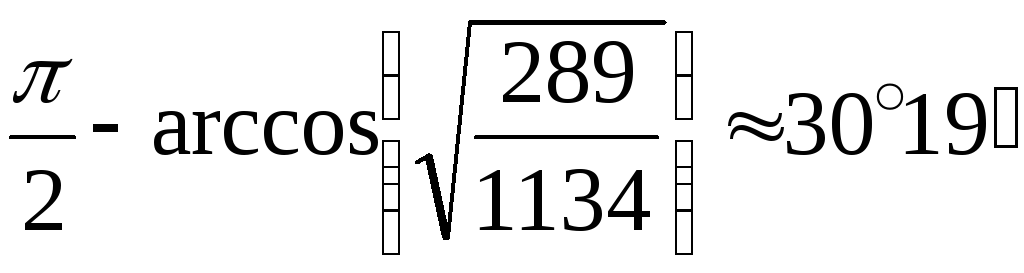 ,
3)
,
3) ,
,
4)
![]() ,
5)
,
5)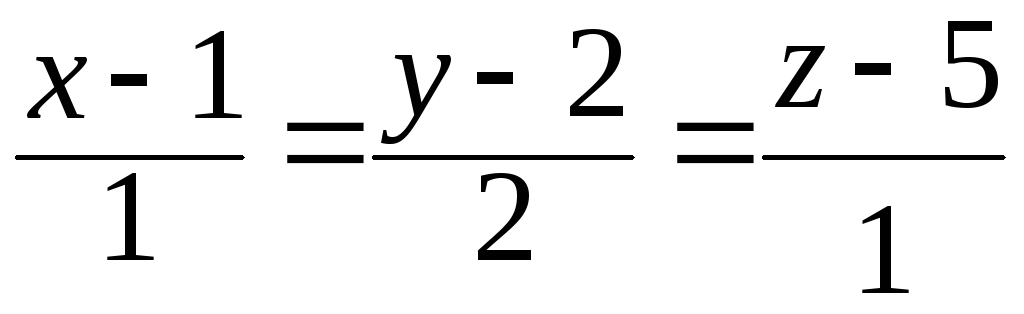 .47.
.47.
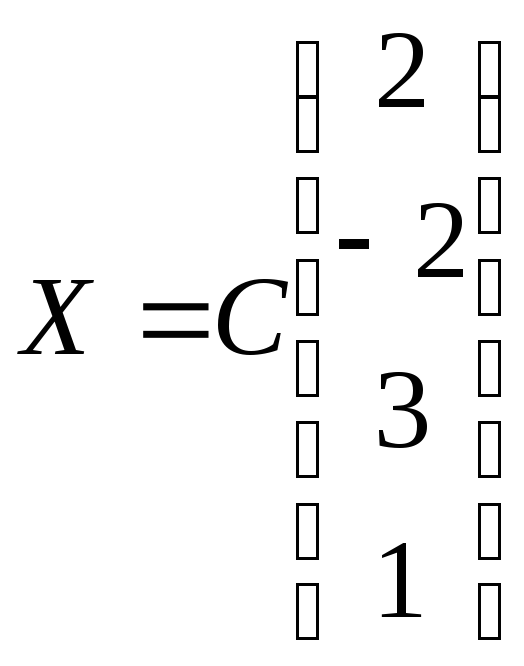 ,
,![]() .
.
48.
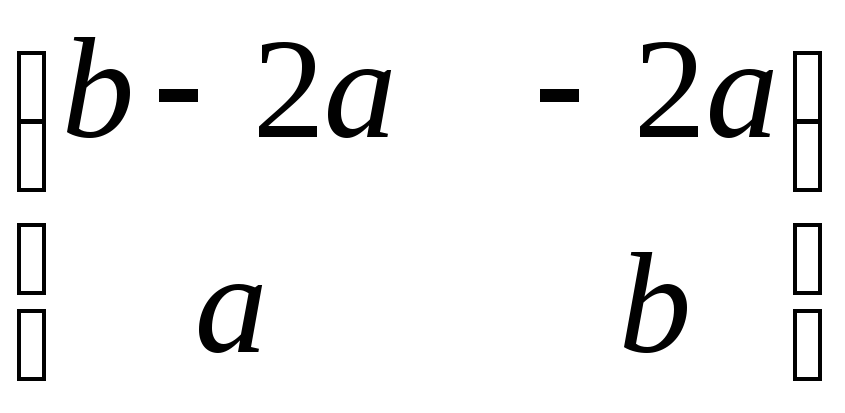 ,где
,где
![]() .
.
49.
 ,
,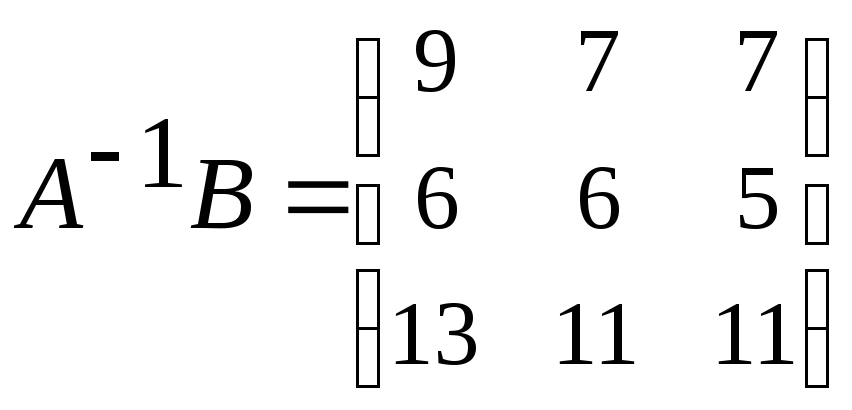 ,
, ,
,
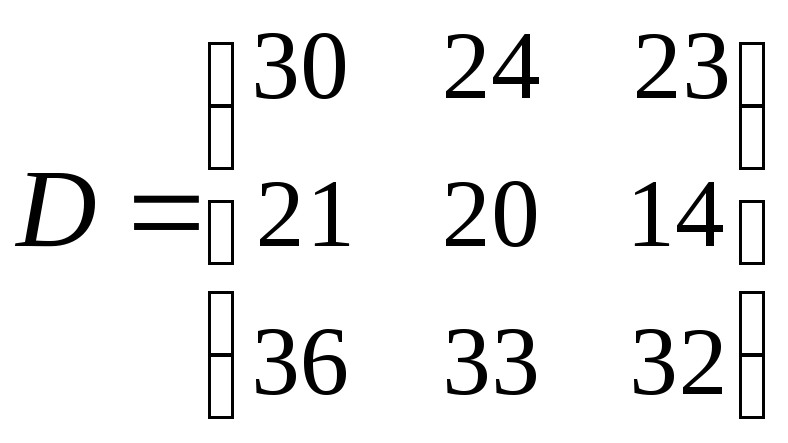 .
50. а)
.
50. а)
![]() ,
б)
,
б)![]() .
51.
.
51.![]() ,
,![]() ,
,![]() .
.
52. а) да,
б) нет.
53.
![]() .
54.нет.
55. а) отражение
трехмерного пространства относительно
начала координат, б)
поворот
трехмерного пространства на угол
.
54.нет.
55. а) отражение
трехмерного пространства относительно
начала координат, б)
поворот
трехмерного пространства на угол
![]() против часовой стрелки, проходящей
через начало координат и составляющей
с координатными осями равные острые
углы. 56. Оператор
против часовой стрелки, проходящей
через начало координат и составляющей
с координатными осями равные острые
углы. 56. Оператор
![]() линейный;
линейный;
 –его матрица в
базисе
–его матрица в
базисе
![]() ,
,![]() ,
,![]() ,
,![]() .
.
57.
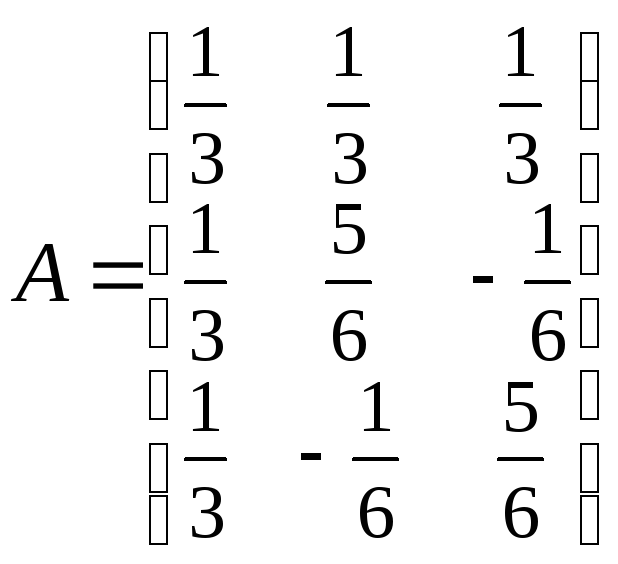 ,
,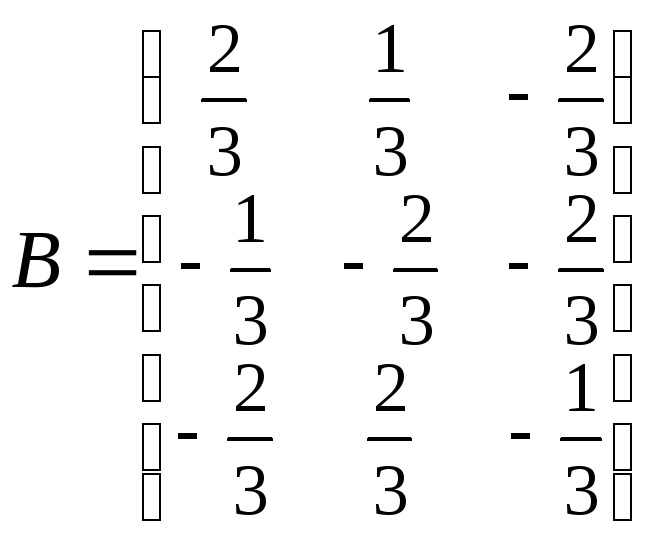 ,
, .
.
58. Собственные
значения:![]() ,
,![]() ,
,![]() ,собственные
векторы: для
,собственные
векторы: для![]()
 ,где
,где ,для
,для![]()
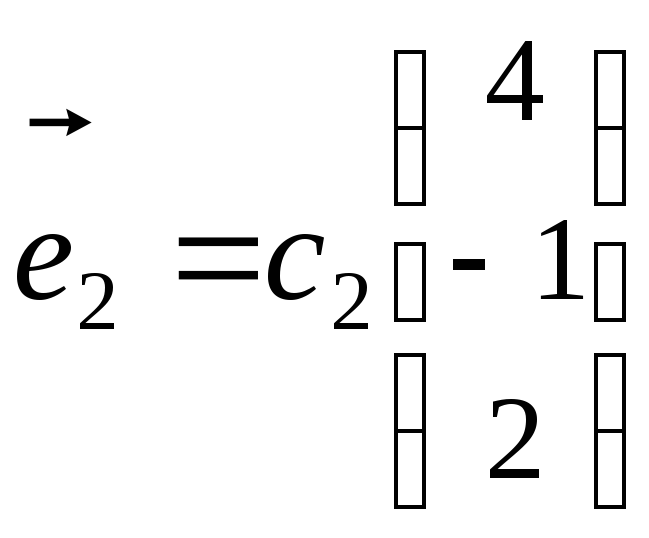 ,где
,где 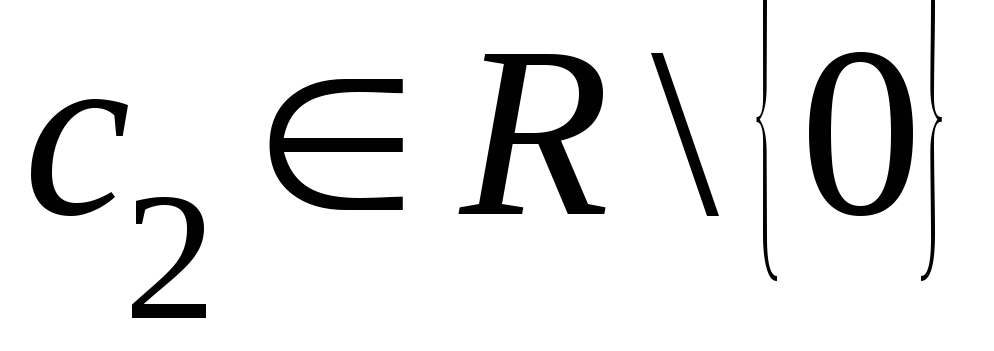 ,для
,для ![]()
 ,где
,где 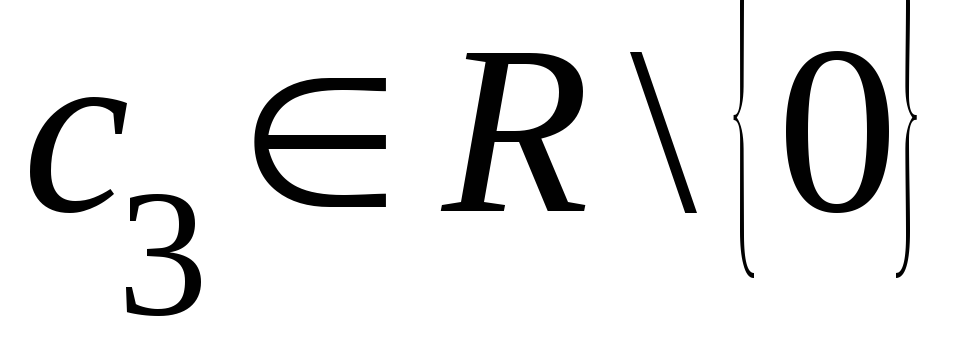 .
.
ВАРИАНТ №20
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ: ПРОСТЕЙШИЕ ЗАДАЧИ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ; ПРЯМАЯ НА ПЛОСКОСТИ; ЛИНИИ ВТОРОГО ПОРЯДКА НА ПЛОСКОСТИ
1. Даны две смежные вершины квадрата А(2, 1) и В(4, 3). Вычислить его площадь.
2. Даны три вершины А(1, 5), В(10, 14), С(9, –1) параллелограмма АВСD, четвертая вершина D противоположна В. определить длину диагоналей этого праллелограмма.
3. Найти координаты точки М1, сииметричной точке М2(–1, 3) относительно прямой, проходящей через точки А(7, 4), В(4, 2).
4. Даны вершины треугольника А(7, 4), В(4, –6), С(8, –3). Составить уравнение его высот.
5. Отрезок, ограниченный точками А(5, –3) и В(11, 0), разделен на три равные части. Определить координаты точек деления.
6. Даны две вершины А(–2, –3) и В(6, –7) треугольника АВС и точка N(5, –3) пересечения его высот. Составить уравнения сторон этого треугольника.
7. Точка А(2,
0) является
вершиной квадрата, диагональ которого
лежит на прямой
![]() .
Составить уравнения сторон этого
квадрата.
.
Составить уравнения сторон этого
квадрата.
8. Составить
уравнения сторон треугольника АВС,
если даны одна из вершин А(2,
–2) и уравнения
двух медиан
![]() .
.
Указание. Убедиться,
что точка А![]() и точкаА
и точкаА![]() .
Пусть
.
Пусть![]() и
и![]() - вершины треугольника, расположеные
на медианах
- вершины треугольника, расположеные
на медианах![]() и
и![]() соответственно, а точки
соответственно, а точки![]() и
и![]() - середины отрезков АВ и АС соответственно.
Далее следует найти координаты вершинВ
и С
треугольника. Так как точки М
и С
лежат на медиане
- середины отрезков АВ и АС соответственно.
Далее следует найти координаты вершинВ
и С
треугольника. Так как точки М
и С
лежат на медиане
![]() ,
то
,
то![]() .
Затем из соотношения
.
Затем из соотношения![]() найдите
найдите![]() ;
далее подставив численное значение
;
далее подставив численное значение![]() в уравнение для
в уравнение для![]() ,
найдите
,
найдите![]() .
Затем, зная
.
Затем, зная![]() и
и![]() ,
найдите
,
найдите![]() по формуле
по формуле![]() .
Далее подставив численное значение
.
Далее подставив численное значение![]() в уравнение для
в уравнение для![]() ,
найдите
,
найдите![]() ,
из соотношения
,
из соотношения![]() найдите
найдите![]() .
Наконец, зная координаты всех вершин
треугольника, найдите общие уравнения
его сторон.
.
Наконец, зная координаты всех вершин
треугольника, найдите общие уравнения
его сторон.
9. Установить, какие линии определяются в полярных координатах следующими уравнениями (построить их на чертеже):
а)![]() ;
б)
;
б)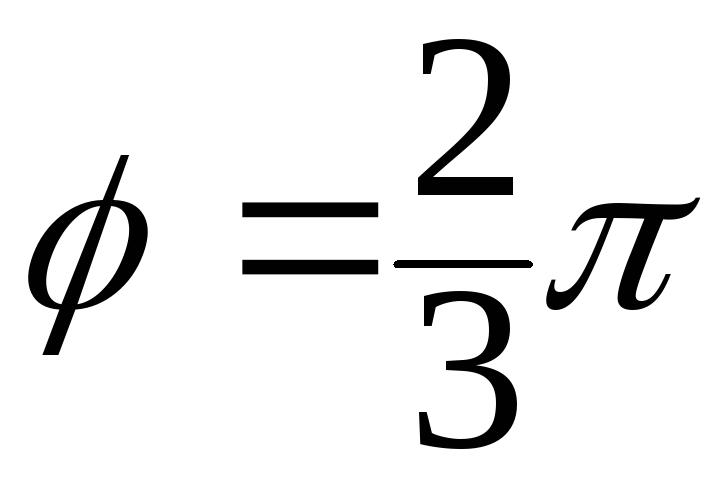 ;
в)
;
в)![]() ;
г)
;
г)![]() ;
;
д)
![]() ;
е)
;
е)![]() .
.
10. Установить,
какая линия определяется уравнением
![]() .
Найти координаты ее центра, полуоси,
эксцентриситет. Сделать чертеж.
.
Найти координаты ее центра, полуоси,
эксцентриситет. Сделать чертеж.
11. Составить
уравнение гиперболы и найти координаты
ее центра и полуоси, если известно, что
левая вершина гиперболы находится в
правом фокусе эллипса:
![]() ,
при этом правая вершина гиперболы
находится в вершине параболы
,
при этом правая вершина гиперболы
находится в вершине параболы![]() ,
эксцентриситет гиперболы равен
,
эксцентриситет гиперболы равен![]() .
.
12. Составить
уравнение линии, для каждой точки которой
расстояние от точки А(4,
2) вдвое меньше
расстояния от прямой
![]() .
Определить, какая это линия; сделать
чертеж.
.
Определить, какая это линия; сделать
чертеж.
13. Линия задана
уравнением
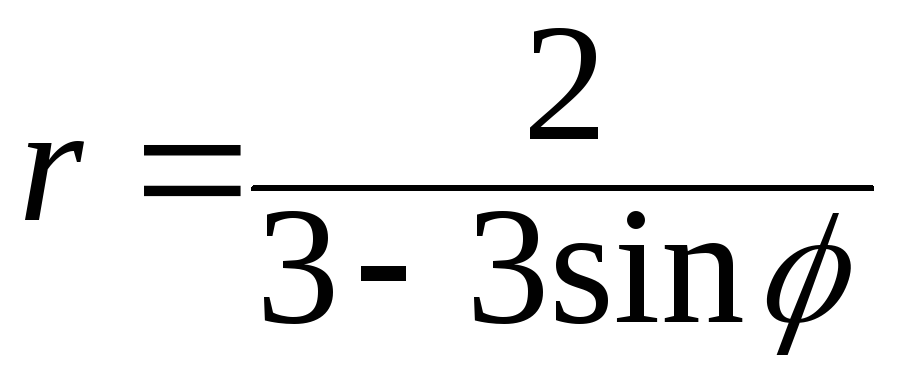 в полярной системе координат.
в полярной системе координат.
Требуется: а)
построить линию по точкам, начиная от
![]() до
до![]() и придавая
и придавая![]() значения через промежуток
значения через промежуток![]() ;
б) найти уравнение данной линии в
декартовой прямоугольной системе
координат, у которой начало совпадает
с полюсом, а положительная полуось
абсцисс – с полярной осью; в) по полученному
уравнению определить, какая это линия.
;
б) найти уравнение данной линии в
декартовой прямоугольной системе
координат, у которой начало совпадает
с полюсом, а положительная полуось
абсцисс – с полярной осью; в) по полученному
уравнению определить, какая это линия.
Определители. Базис в пространстве. Координаты вектора
14. Вычислить определители:
а) по правилу треугольника;
б) разложением по элементам первой строки;
в) разложением по элементам второго столбца;
г) сведением к треугольному виду:
а)
 ,
б)
,
б) ,
в)
,
в) ,
г)
,
г)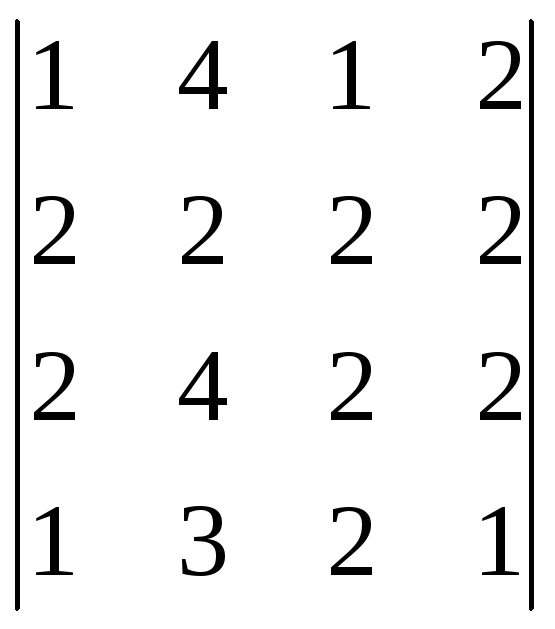 .
.
15.
Даны векторы:
![]() 1=(1,
3, 2);
1=(1,
3, 2);
![]() 2=(0,
–1, –1);
2=(0,
–1, –1);
![]() 3=(–2,
0, 1);
3=(–2,
0, 1);
![]() =(–4,
8,
9)
в некотором базисе. Показать, что первые
три вектора сами образуют базис и найти
координаты вектора
=(–4,
8,
9)
в некотором базисе. Показать, что первые
три вектора сами образуют базис и найти
координаты вектора
![]() в этом базисе.
в этом базисе.
3. Линейные операции над векторами. Проекция вектора на ось. Скалярное, векторное и смешанное произведения векторов.
16. Найти координаты
единичного вектора (орта)
![]() ,
сонаправленного с вектором
,
сонаправленного с вектором
![]() =(3,
4, 2).
=(3,
4, 2).
17. Два вектора
![]() =(–2,
3, –6)и
=(–2,
3, –6)и
![]() =(1,
–2, 2) приложены
к одной точке. Найти координаты:
=(1,
–2, 2) приложены
к одной точке. Найти координаты:
а) ортов
![]() и
и![]() векторов
векторов![]() и
и![]() ;
;
б) вектора
![]() +
+![]() ;
;
в)
вектора
![]() ,
направленного по биссектрисе угла между
векторами
,
направленного по биссектрисе угла между
векторами![]() и
и![]() при условии, что
при условии, что![]() .
.
18.
Найти проекцию вектора ![]() =(3,
–1, –2)
на направление вектора
=(3,
–1, –2)
на направление вектора
![]() =(–1,
2, 2).
=(–1,
2, 2).
19.
Найти проекцию вектора
![]() на ось, составляющую с координатными
осями
на ось, составляющую с координатными
осями![]() и
и![]() углы
углы![]() ,
,![]() ,
а с осью
,
а с осью![]() тупой угол
тупой угол![]() .
.
20.
Дан квадрат ABCD
(обозначение вершин принято по ходу
часовой стрелки), длина стороны которого
равна
![]() .
ТочкаО
выбрана в плоскости квадрата так, что
.
ТочкаО
выбрана в плоскости квадрата так, что
![]() ,
,![]() .
Найти
.
Найти![]() .
.
Указание. Использовать последовательность действий:
а)
ввести декартову прямоугольную систему
координат
![]() с
началом в точке О так, чтобы ось
с
началом в точке О так, чтобы ось![]() была направлена по вектору
была направлена по вектору![]() ,
а ось
,
а ось![]() направить в сторону расположения
квадрата;
направить в сторону расположения
квадрата;
б)
подсчитав длину
![]() диагонали квадрата, убедиться (по теореме
Пифагора), что
диагонали квадрата, убедиться (по теореме
Пифагора), что![]() - прямоугольный (
- прямоугольный (![]() ),
а поэтому
),
а поэтому![]() ;
;
в)
найти координаты вектора
![]() ,
найти координаты векторов
,
найти координаты векторов![]() и
и![]() (очевидно
(очевидно![]() ),
используя равенство
),
используя равенство![]() ,
найти координаты вектора
,
найти координаты вектора![]() ;
;
г)
зная координаты векторов
![]() и
и![]() ,
найти
,
найти![]() ,
где
,
где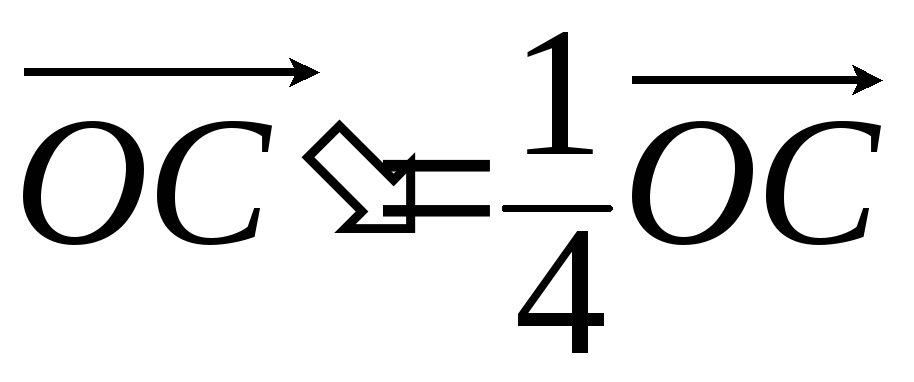 ,
,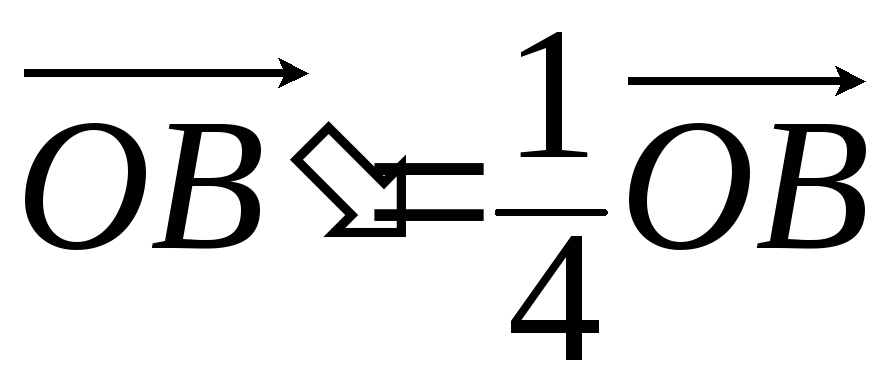 .
.
21.
Векторы
![]() и
и![]() являются сторонами параллелограммаОАСВ.
Точка N
– середина стороны ВС.
Найти
являются сторонами параллелограммаОАСВ.
Точка N
– середина стороны ВС.
Найти
![]() .
.
22.
Дано
![]() ,
,![]() ,
,![]() .
Найти
.
Найти![]() и величину угла между векторами
и величину угла между векторами![]() и
и![]() ,
если
,
если![]() .
.
23. Вычислить
координаты векторного произведения
![]() и его длину
и его длину![]() ,
если
,
если
![]() =(3,
–4, 2),
=(3,
–4, 2),
![]() .
.
24. Даны вершины треугольника А(–1, 3, –1), В(2, 1, 5) и С(–4, 2, 7). Найти площадь треугольника и длину высоты, опущенной из вершины А.
25.
Вектор
![]() ,
ортогонален к оси
,
ортогонален к оси![]() и вектору
и вектору
![]() (–2,
3, 1)
и образует
с осью
(–2,
3, 1)
и образует
с осью
![]() острый угол. Найти координаты вектора
острый угол. Найти координаты вектора![]() ,
если
,
если![]() .
.
26. Найти площадь
параллелограмма, построенного на
векторах
![]() и
и![]() ,
если
,
если![]() ,
,![]() и
и![]() .
.
27. Вычислить
смешанное произведение векторов
![]() ,
,
![]() (–2,
0, 1),
(–2,
0, 1),![]() (0,
2, 3).
(0,
2, 3).
28. В правом базисе
![]() заданы векторы:
заданы векторы:![]() ,
,![]() ,
,![]() .
Показать, что эти три вектора не
компланарны; установитьориентацию
тройки векторов
.
Показать, что эти три вектора не
компланарны; установитьориентацию
тройки векторов![]() .
.
29. Вычислить объем пирамиды, вершины которой А(1, 2, 3), В(–1, 5, –3), С(1, 2, 3), D(1, 5, 5).
30. Вектор
![]() перпендикулярен к векторам
перпендикулярен к векторам![]() и
и![]() .
Вычислить
.
Вычислить![]() ,
если
,
если
![]() ,
,![]() ,
,![]() ,
,![]() ,а тройка
векторов
,а тройка
векторов
![]() –
левая.
–
левая.
4. Аналитическая геометрия в пространстве: плоскость и прямая в пространстве; поверхности второго порядка
31.
Составить
уравнение плоскости, проходящей через
точку М0(–2,
4, 1), параллельную
плоскости
![]() .
.
32. Составить
уравнение плоскости, проходящей через
точку М0(–2,
4, 1) и прямую
 .
.
33. Составить
уравнение плоскости, проходящей через
прямую
 перпендикулярно плоскости
перпендикулярно плоскости![]() .
.
34. Составить
уравнение плоскости, которая проходит
через точку М0(–3,
–1, 5) перпендикулярно
к двум плоскостям
![]() и
и![]() .
.
35. Найти расстояние
![]() от точкиМ0(5,
8, 5) до плоскости
от точкиМ0(5,
8, 5) до плоскости
![]() .
.
36. Даны вершины треугольника А(6, 0, 2), В(8, 3, 2), С(6, –3, –1). Составить канонические уравнения биссектрисы его внутреннего угла при вершине В.
37. На оси
![]() найти координаты точек, отстоящих от
плоскости
найти координаты точек, отстоящих от
плоскости![]() на расстоянии
на расстоянии![]() =6.
=6.
38. Составить
канонические уравнения прямой, проходящей
через точку М0(3,
–4, –5),
параллельно прямой
![]() ,
,![]() ,
,![]() .
.
39. Найти координаты
точки пересечения прямой
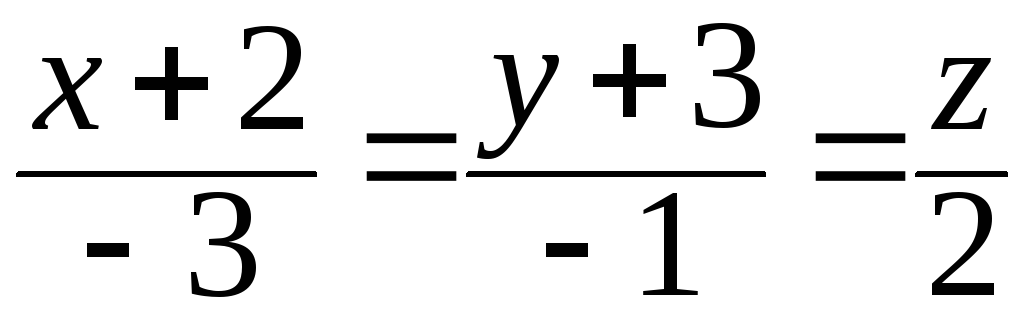 и плоскости
и плоскости![]() .
.
40. Найти проекцию
точки Р(2, –1,
6) на прямую
![]() ,
,![]() ,
,![]() .
.
41. Найти координаты
точки Q,
симметричной точке Р(–2,
1, 6) относительно
плоскости
![]() .
.
42. Найти координаты
точки Q,
симметричной точке Р(2,
6, –1) относительно
прямой
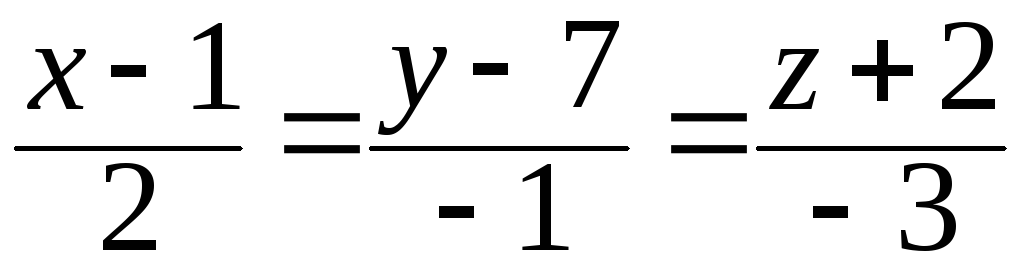 .
.
43. Вычислить
растояние
![]() от точкиР(–1,
5, –3) до прямой
от точкиР(–1,
5, –3) до прямой
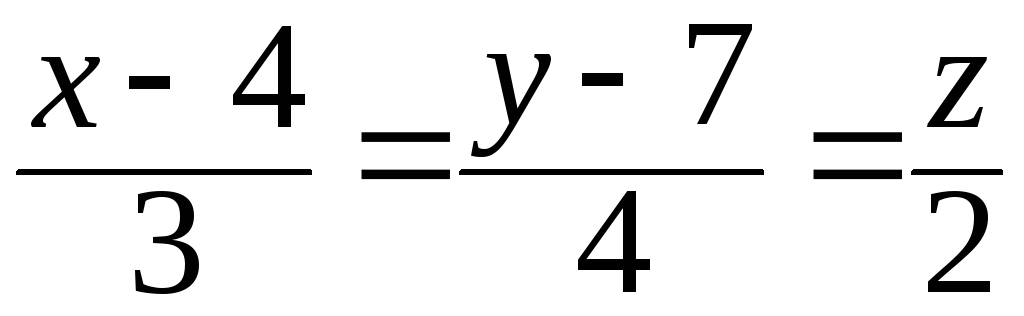 .
.
44. Найти канонические
уравнения прямой
![]() ,
которая проходит через точкуМ0(0,
–1, 2) параллельно
плоскости
,
которая проходит через точкуМ0(0,
–1, 2) параллельно
плоскости
![]() и пересекает прямую
и пересекает прямую![]() .
.
Указание. Использовать последовательность действий:
а) составить
уравнение плоскости
![]() ,
проходящей через точкуМ0,
параллельную плоскости
,
проходящей через точкуМ0,
параллельную плоскости
![]() ;
;
б) найти координаты
точки М1
пересечения прямой
![]() с плоскостью
с плоскостью![]() (см. задачу 39);
(см. задачу 39);
в) составить канонические уравнения прямой, проходящей через точки М0 и М1.
45. Даны координаты вершин пирамиды А1(–1, –1, 5), А2(1, 4, 2), А3(4, 1, 1), А4(2, 3, 6). Найти: 1) угол между ребрами А1А2 и А1А4; 2) угол между ребром А1А4 и гранью А1А2А3; 3) уравнение прямой А1А2; 4) уравнение плоскости А1А2А3; 5) уравнение высоты, опущенной из вершины А4 на грань А1А2А3.
46. Построить эскиз тела, ограниченного поверхностями:
а)
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
б)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
5. Элементы линейной алгебры: системы линейных уравнений; матрицы; линейное векторное пространство; линейные операторы
47. Решить систему линейных уравнений методом Гаусса

48. Найти все
вещественные матрицы, перестановочные
с матрицей
![]() .
.
49. Найти матрицу
![]() ,
где
,
где
А=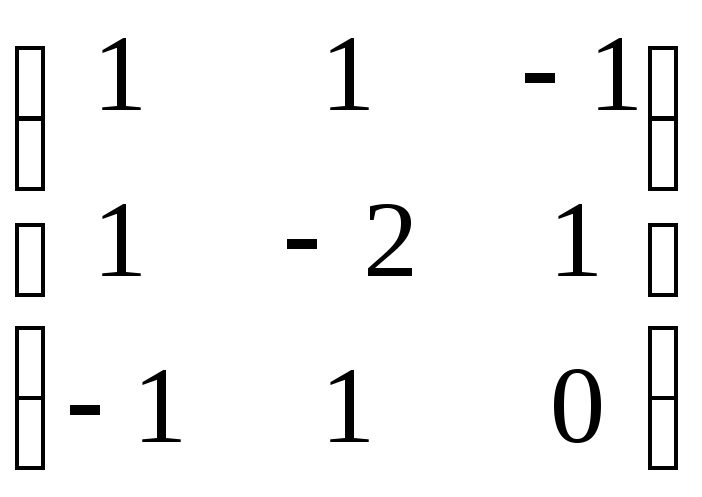 ,
В=
,
В=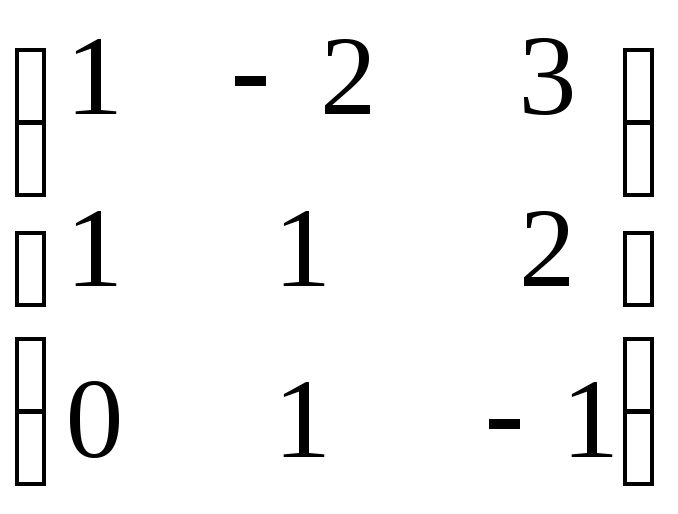 ,
С=
,
С=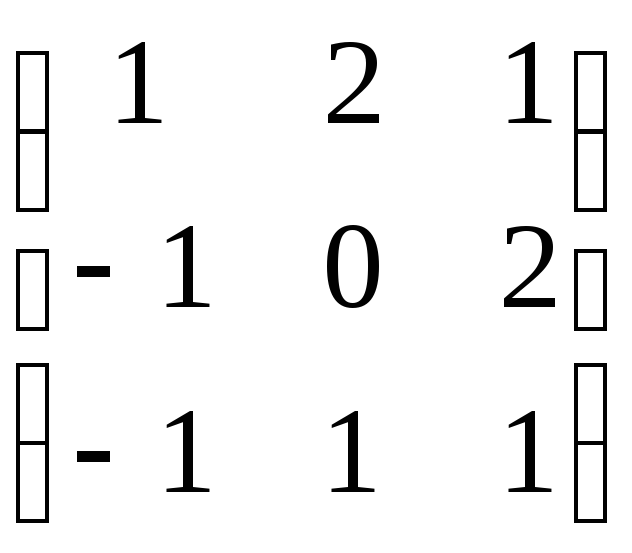 .
.
50. Найти ранг матриц:
а)
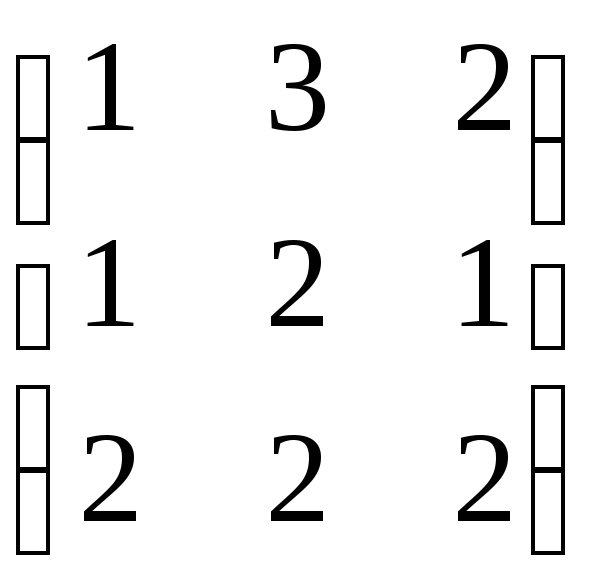 ;
б)
;
б) .
.
51. Дана система линейных уравнений
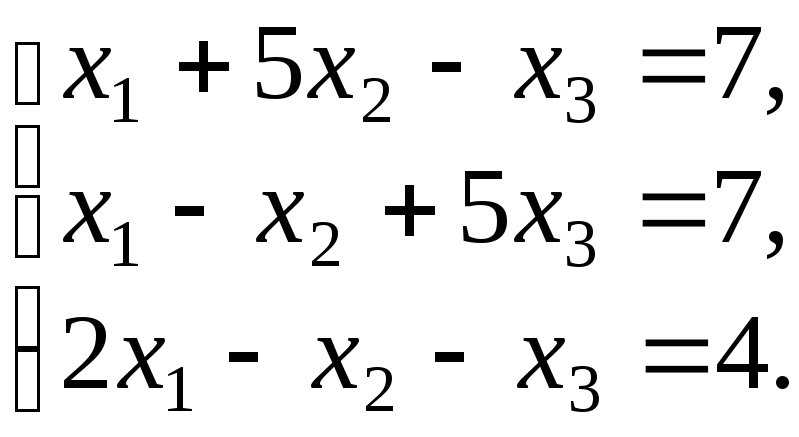
Доказать ее совместность и решить тремя способами: а) методом Гаусса; б) средствами матричного исчисления; в) по формулам Крамера.
52. Является ли вещественными линейными пространствами:
а) множество всех
вещественных матриц второго порядка
вида
![]() ,
где
,
где![]() ;
;
б) множество всех
вещественных матриц второго порядка
вида
![]() ,
где
,
где![]() ;
;
53. Найти все значения
![]() ,
при которых вектор
,
при которых вектор![]() линейно выражается через векторы
линейно выражается через векторы![]() ,
если
,
если
![]() =(2,
–1, 2),
=(2,
–1, 2),![]() =(1,
–2, 2),
=(1,
–2, 2),![]() =(2,
–1, 1),
=(2,
–1, 1),![]() =(1,
2,
=(1,
2,![]() ).
).
54. Выяснить, является
ли данная система векторов из
![]() линейно зависимой?
линейно зависимой?
![]() =(1,
2, 0, –1),
=(1,
2, 0, –1),![]() =(2,
1, 1, 1),
=(2,
1, 1, 1),![]() =(1,
2, 4, –1),
=(1,
2, 4, –1),![]() =(2,
4, 4, –2).
=(2,
4, 4, –2).
55. Выяснить
геометрический смысл действия линейных
операторов, данных в пространстве
![]() ,
матрицы которых относительно
ортонормированного базиса
,
матрицы которых относительно
ортонормированного базиса![]() имеют вид:
имеют вид:
а)
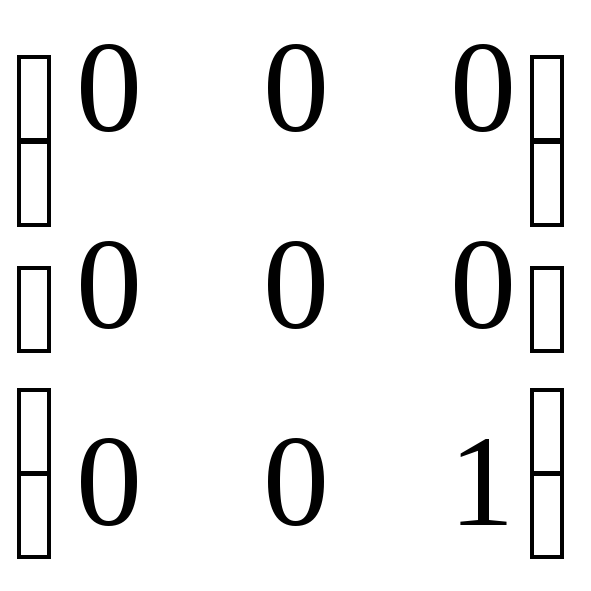 ;
б)
;
б)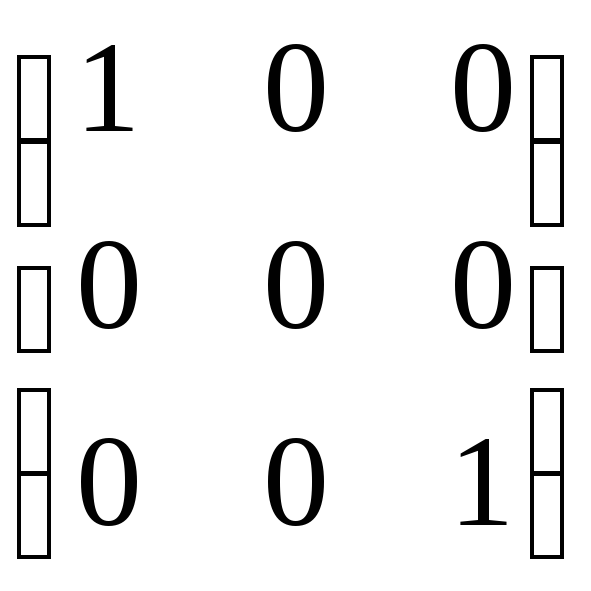 .
.
56. В пространстве
Р2
всех многочленов степени
![]() вида
вида![]() ,
где
,
где![]() оператор
оператор![]() действует так:
действует так:![]() .
Доказать, что оператор
.
Доказать, что оператор![]() линеен и найти его матрицу в базисе
линеен и найти его матрицу в базисе![]() ,
,![]() ,
,![]() .
.
57. В обычном
пространстве линейный оператор
![]() зеркально отражает векторы относительно
прямой
зеркально отражает векторы относительно
прямой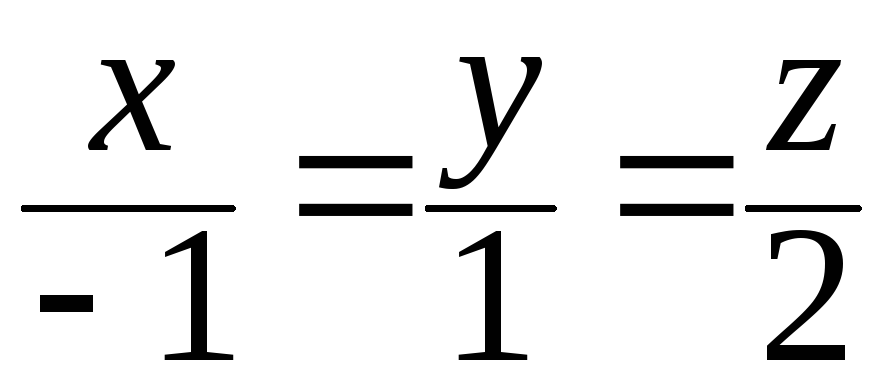 ,
а линейный оператор
,
а линейный оператор![]() ортогонально проецирует векторы на
плоскость
ортогонально проецирует векторы на
плоскость![]() .
Найти матрицы линейных операторов
.
Найти матрицы линейных операторов![]() ,
,![]() ,
,![]() в базисе
в базисе![]() .
.
58. Найти собственные
значения и собственные векторы линейного
преобразования, заданного в некотором
базисе матрицей
 .
.
