
Lektsii_Chast3
.pdfГосударственное образовательное учреждение высшего профессионального образования "Тольяттинский государственный университет"
Кафедра «Общая и теоретическая физика»
КУРС ЛЕКЦИЙ ПО ДИСЦИПЛИНЕ «ФИЗИКА»
ЧАСТЬ 3
для студентов технических специальностей
Составил:
доцент кафедры «Общая и теоретическая физика» ТГУ Сарафанова В.А.
Тольятти 2014
ОГЛАВЛЕНИЕ |
|
РАЗДЕЛ 4. КОЛЕБАНИЯ И ВОЛНЫ. ОПТИКА. ЯДРО................................................ |
4 |
Глава 4.1. КОЛЕБАНИЯ И ВОЛНЫ .............................................................................. |
4 |
§ 1. Гармонические колебания, их характеристики .................................................. |
4 |
§ 2. Механические гармонические колебания............................................................ |
5 |
§ 3. Электромагнитные гармонические колебания.................................................... |
7 |
§ 4. Свободные затухающие колебания ...................................................................... |
9 |
§ 5. Вынужденные колебания..................................................................................... |
10 |
§ 6. Резонанс ................................................................................................................. |
11 |
§ 7. Волны..................................................................................................................... |
12 |
Глава 4.2. ВОЛНОВАЯ ОПТИКА ................................................................................ |
16 |
§ 1. Интерференция света ........................................................................................... |
16 |
§ 2. Способы получения когерентных источников.................................................. |
18 |
§ 3. Расчет интерференционной картины от двух когерентных источника ......... |
19 |
§ 4. Интерференция в тонких пленках ...................................................................... |
20 |
§ 5. Дифракция света ................................................................................................... |
22 |
§ 6. Метод зон Френеля............................................................................................... |
23 |
§ 7. Дифракция Френеля ............................................................................................. |
24 |
§ 8. Дифракция Фраунгофера на одной щели .......................................................... |
26 |
§ 9. Дифракция Фраунгофера на дифракционной решетке .................................... |
27 |
§ 10. Дифракция на пространственной решетке ...................................................... |
29 |
§ 11. Поляризация света.............................................................................................. |
30 |
§ 12. Поляризация света при отражении и преломлении. Закон Брюстера .......... |
32 |
§ 13. Двойное лучепреломление ................................................................................ |
33 |
§ 14. Поляризационные призмы и поляроиды ......................................................... |
34 |
Глава 4.3. КВАНТОВАЯ ПРИРОДА ИЗЛУЧЕНИЯ................................................... |
36 |
§ 1. Тепловое излучение и его характеристики........................................................ |
36 |
§ 2. Экспериментальные законы теплового излучения ........................................... |
38 |
§ 3 Формулы Рэлея-Джинса и Планка....................................................................... |
39 |
§ 4. Фотоэффект ........................................................................................................... |
41 |
§ 5. Уравнение Эйнштейна для внешнего фотоэффекта......................................... |
42 |
§ 6. Фотон и его характеристики ............................................................................... |
43 |
§ 7. Эффект Комптона................................................................................................. |
44 |
§ 8. Корпускулярно-волновой дуализм электромагнитного излучения ................ |
46 |
Глава 4.4. ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ................................................ |
47 |
§ 1. Гипотеза де Бройля............................................................................................... |
47 |
§ 2. Соотношение неопределённостей ...................................................................... |
48 |
§ 3. Волновая функция и её статистический смысл ................................................ |
49 |
§ 4. Уравнение Шредингера ....................................................................................... |
50 |
§ 5. Туннельный эффект.............................................................................................. |
51 |
§ 6. Частица в одномерной прямоугольной «потенциальной яме» ....................... |
52 |
§ 7. Атом водорода в квантовой механике ............................................................... |
54 |
§ 8. Квантовые числа ................................................................................................... |
55 |
§ 9. Спектр атома водорода ........................................................................................ |
56 |
2
§ 10. |
Поглощение, спонтанное и вынужденное излучение. .................................. |
57 |
|
§ 11. |
Лазер .................................................................................................................... |
58 |
|
Глава 4.5. АТОМНОЕ ЯДРО......................................................................................... |
59 |
||
§ 1. Строение атомных ядер ....................................................................................... |
59 |
||
§ 2. Дефект массы и энергия связи ядра ................................................................... |
60 |
||
§ 3. Модели атомного ядра ......................................................................................... |
62 |
||
§ 4. Ядерные силы ....................................................................................................... |
63 |
||
§ 5. Радиоактивность ................................................................................................... |
64 |
||
§ 6. |
Закон радиоактивного распада (превращения) ................................................. |
64 |
|
§ 7. |
Альфа-распад ........................................................................................................ |
67 |
|
§ 8. |
Бета-распад............................................................................................................ |
67 |
|
§ 9. |
Активность радиоактивного вещества............................................................... |
69 |
|
§ 10. |
Ядерные реакции ................................................................................................ |
69 |
|
3

РАЗДЕЛ 4. КОЛЕБАНИЯ И ВОЛНЫ. ОПТИКА. ЯДРО
Глава 4.1. КОЛЕБАНИЯ И ВОЛНЫ
§ 1. Гармонические колебания, их характеристики
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени.
При колебательном движении маятника изменяется координата его центра масс, в случае переменного тока изменяются напряжение и ток в цепи. Однако, различные по физической природе колебания описываются одинаковыми характеристиками и уравнениями. Отсюда существует единый подход к изучению колебаний различной физической природы.
Колебания называются свободными или собственными, если они совершаются за счет первоначально сообщенной энергии при отсутствии внешних воздействий на колебательную систему.
Простейший тип колебаний: гармонические колебания - колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса.
Гармонические колебания описываются уравнением:
S Acos( 0t ) ,
где S - колеблющаяся величина;
А- амплитуда колебаний - максимальное значение колеблющейся величины;
0 - круговая (циклическая) частота;
- начальная фаза колебаний в момент времени t=0;
( 0t ) - фаза колебаний в момент времени t.
Определенные состояния системы повторяются через промежуток времени Т - период колебаний.
Период колебаний Т - время, за которое фаза колебаний получает приращение 2 :
|
|
|
|
(t T ) ( |
t ) 2 , |
T |
2 |
|
. |
|
|
|||||||||||||
0 |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Частота колебаний |
|
- число полных колебаний, совершаемых в единицу |
||||||||||||||||||||||
времени: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
||
Связь циклической частоты, периода и частоты: |
0 |
|
2 |
2 |
. |
|||||||||||||||||||
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
Продифференцировав уравнение гармонических колебаний, получим |
||||||||||||||||||||||||
скорость изменения величины S: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
dS |
A |
|
sin( |
|
t ) A |
|
cos( |
|
t ) . |
||||||||||||||
|
|
0 |
0 |
0 |
0 |
|||||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Продифференцировав уравнение гармонических колебаний дважды, получим ускорение изменения S:
4
|
d 2 S |
A 2 cos( |
|
t ) A |
2 cos( |
|
t ) . |
|
|||||
|
|
0 |
0 |
|
|||||||||
|
dt 2 |
0 |
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
, а фаза |
|
||
Фаза скорости отличается от фазы величины |
S на |
ускорения |
|||||||||||
отличается от фазы S на . |
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
Из последнего уравнения вытекает дифференциальное уравнение |
|||||||||||||
гармонических колебаний: |
|
|
d 2 S |
02 S 0 |
, |
решением |
которого |
является: |
|||||
|
|
dt 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S Acos( 0t ) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
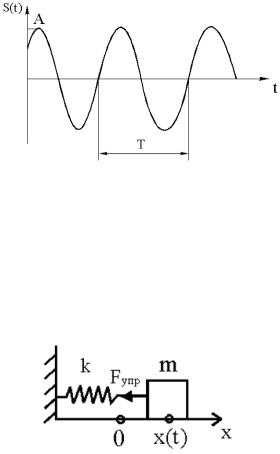
График гармонического колебания: |
|
|
|
|
|
||||||||
§ 2. Механические гармонические колебания
Примером механических гармонических колебаний являются колебания пружинного маятника.
Пружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы: F kx, где k - коэффициент упругости, в случае пружины k называется жесткостью, x – отклонение груза от положения равновесия.
Колеблющейся величиной в данном случае является координата x груза. Зависимость координаты x от времени t задается уравнением гармонических
колебаний:
|
|
|
x Acos( 0t ) |
. |
|
|
|
|
|
|
||||
Скорость изменения координаты от времени: V x |
dx |
A |
|
sin( |
|
t ) . |
||||||||
|
0 |
0 |
||||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ускорение: a x |
d 2 x |
A 2 cos( |
|
t ) 2 x . |
|
|
|
|
||||||
|
0 |
|
|
|
|
|||||||||
|
dt 2 |
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда дифференциальное |
уравнение |
колебаний пружинного маятника: |
||||||||||||
x 02 x 0 .
5

|
|
Умножим обе части уравнения |
a 2 x |
на массу m груза: ma m 2 x . По 2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
||||
закону Ньютона: |
F ma . |
Следовательно, упругая |
сила: F kx m 2 x , а |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
коэффициент упругости: |
k m 2 . Отсюда для пружинного маятника: циклическая |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||
частота |
0 |
|
|
|
k |
|
|
, период |
T |
2 |
|
2 |
m |
|
|
. |
|
||||||||||||
|
|
m |
|
k |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Рассмотрим колебания с энергетических позиций. При отклонении маятника |
|||||||||||||||||||||||||||
от |
положения |
равновесия |
увеличивается его |
потенциальная энергия: |
|||||||||||||||||||||||||
|
|
kx2 |
|
m 2 x2 |
|
m 2 A2 |
cos2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
Eп |
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
( 0t ) |
. Если его отпустить, то под действием |
|||||||||||||
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
силы упругости он возвращается к положению равновесия, при этом его
потенциальная |
|
энергия |
превращается |
в |
кинетическую: |
|||||||
|
mV 2 |
|
mA2 2 |
|
|
|
|
|
|
|
||
Eк |
|
|
|
0 |
sin 2 |
( 0t ) |
. |
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
mA2 2 |
|
|
|
Полная энергия груза в любой момент времени: |
E Eк Eп |
0 |
|
. |
|||||||
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При гармонических колебаниях справедлив закон сохранения механической |
|||||||||||
энергии, так как упругая сила консервативна. |
|
|
|
|
||||||||
|
Силы, имеющие другую природу, чем упругие силы, но удовлетворяющие |
|||||||||||
выражению: F kx, называются квазиупругими. |
|
|
|
|
||||||||
|
Таким образом, гармонические колебания совершаются под действием только |
|||||||||||
упругой или квазиупругой силы. |
|
|
|
|
|
|||||||
|
Любая сила прямо пропорциональная смещению и направленная к |
|||||||||||
положению равновесия называется возвращающей силой. |
|
|
|
|||||||||
|
Математическим |
маятником называется |
идеализированная система, |
|||||||||
состоящая из невесомой и нерастяжимой нити, на которой подвешена материальная точка, колеблющаяся под действием силы тяжести.
Если маятник отклонить от положения равновесия и отпустить без начальной скорости, то он будет совершать колебания в вертикальной плоскости по дуге окружности.
Уравнение движения математического маятника можно получить, используя уравнение динамики вращательного движения:
|
|
|
|
J M , |
|
|||
где |
M Fl - |
момент силы, |
стремящейся вернуть маятник в |
|||||
положения равновесия, |
F mg sin - возвращающая сила. Так |
|||||||
как |
направления силы |
|
и отклонения от |
положения |
||||
F |
||||||||
равновесия противоположны, |
отсюда |
знак |
минус «-». |
d 2 |
- угловое |
|||
dt 2 |
||||||||
|
|
|
|
|
|
|
||
ускорение; J ml 2 - момент инерции маятника относительно оси вращения.
6

Тогда: ml 2 |
d 2 |
mgl sin ; |
d 2 |
|
g |
sin 0 . При малых колебаниях: |
dt 2 |
dt 2 |
|
||||
|
|
|
l |
|||
sin . Следовательно, дифференциальное уравнение гармонических колебаний
математического |
маятника: |
|
d 2 |
|
|
g |
0 . |
Обозначив |
|
g |
02 , |
получим |
||||||||||
|
dt 2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
l |
|
||||
дифференциальное |
уравнение: |
|
d 2 |
|
02 0 , |
решением |
которого |
является: |
||||||||||||||
|
dt 2 |
|
||||||||||||||||||||
Acos( 0t ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
То есть при малых колебаниях угловое смещение |
||||||||||||||||||||||
математического маятника меняется по гармоническому закону. |
|
|
|
|
||||||||||||||||||
|
Для математического |
маятника |
циклическая частота: |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
g |
|
, период: |
T 2 |
l |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Физический маятник – это твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси подвеса, не проходящей через центр масс тела.
§ 3. Электромагнитные гармонические колебания
Рассмотрим колебательный контур – цепь, состоящую из включенных последовательно катушки индуктивностью L, конденсатора емкости С и резистора сопротивлением R.
Идеальный колебательный контур, в котором сопротивление пренебрежимо мало R 0.
Для возбуждения в контуре колебаний конденсатор заряжают, сообщая его обкладкам заряды q . В начальный момент t 0 между обкладками конденсатора
возникнет электрическое поле, энергия которого E |
|
|
q 2 |
. Если замкнуть |
|
эл |
2C |
||||
|
|
|
|||
|
|
|
|
конденсатор на катушку индуктивности, он начнет разряжаться, и в контуре потечет возрастающий со временем ток. В результате энергия электрического поля будет
уменьшаться, |
а энергия магнитного поля E |
|
|
1 |
LI 2 |
|
1 |
Lq 2 |
возрастать. Если |
||||||||
магн |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
||
R 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
то |
энергия не |
тратится |
на |
нагревание |
и |
полная энергия: |
|||||||||||
E |
1 |
q2 |
1 |
Lq2 |
const остается постоянной. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||
|
2С |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
момент |
времени |
t |
1 |
T |
конденсатор полностью |
|
|||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
разрядится, энергия электрического поля обращается в ноль, а энергия магнитного поля (и ток) достигает наибольшего значения. Начиная с этого момента ток в контуре будет убывать, следовательно, ослабевает магнитное поле катушки. Согласно правилу Ленца в ней индуцируется ток в том же направлении, что и ток разрядки конденсатора. Конденсатор начнет
7

перезаряжаться, заряд на обкладках конденсатора достигнет максимума.
Далее те же процессы начнут протекать в обратном направлении, и к моменту времени t T система придет в первоначальное состояние. После этого начнется повторение цикла разрядки и зарядки конденсатора.
Периодически изменяющиеся при этом величины: заряд q на обкладках
конденсатора, напряжение U на |
конденсаторе и сила |
тока I |
через катушку |
индуктивности. |
|
|
|
Электрические колебания |
в колебательном |
контуре |
аналогичны |
механическим колебаниям маятника. Энергия электрического поля конденсатора
E |
|
|
q 2 |
|
E |
|
|
|
kx2 |
аналогична потенциальной энергии |
упругой деформации; |
|||||||||||||
эл |
|
п |
|
|
||||||||||||||||||||
|
|
|
2C |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
энергия |
|
|
магнитного |
поля |
катушки |
E |
|
|
1 |
LI 2 |
|
1 |
Lq 2 |
|||||||||||
|
|
магн |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
E |
|
|
mV 2 |
|
|
mx |
2 |
аналогична |
кинетической энергии маятника. |
Сила |
тока в |
|||||||||||||
к |
|
2 |
|
|
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
контуре |
|
I V |
|
|
аналогична скорости движения маятника; |
индуктивность играет |
||||||||||||||||||
роль |
|
массы |
L m , |
а сопротивление |
контура играет |
роль |
силы |
трения, |
||||||||||||||||
действующей на маятник R Fтр .
Согласно закону Ома (2 правилу Кирхгофа): IR UC S . Сопротивление в
контуре |
отсутствует |
R 0, |
|
напряжение |
|
на |
конденсаторе: |
U |
|
|
q |
, ЭДС |
|||||||||||||||||||||
C |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
самоиндукции по закону Фарадея: |
|
|
|
L |
dI |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставим в |
уравнение |
|
и |
получим |
дифференциальное |
уравнение |
|||||||||||||||||||||||||||
|
|
|
|
|
|
q |
|
|
|
|
|
dI |
|
|
|
|
|
q |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
L dt |
|
Lq |
C |
0 |
LC q |
|
|
|
|
|
|||||||||||||||
электрических колебаний: |
|
C |
; |
или |
q |
|
0 |
. |
|
Отсюда |
|||||||||||||||||||||||
вытекает |
уравнение |
гармонических |
колебаний |
|
колебательного |
контура: |
|||||||||||||||||||||||||||
|
|
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
q qmax cos( 0t ) |
, где |
|
|
|
|
- циклическая частота или собственная частота |
|||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
LC |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
контура. Период колебательного контура: T |
|
2 |
|
|
|
||||||||||||||||||||||||||||
|
|
LC - формула Томпсона. |
|||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Продифференцировав уравнение гармонических колебаний, получим |
|||||||||||||||||||||||||||||||||
выражение для силы тока: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
I q 0qmax sin( 0t ) Imax sin( 0t ) . |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Найдем зависимость напряжения на конденсаторе от времени:
U |
|
|
q |
|
|
qmax |
cos( |
|
t ) U |
|
cos( |
|
t ) . |
|||
C |
|
|
|
0 |
max |
0 |
||||||||||
|
|
C |
|
C |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Математический, пружинный, физический маятники, колебательный контур |
||||||||||||||||
являются примерами гармонического осциллятора. |
|
|
|
|
||||||||||||
Гармоническим |
осциллятором |
называется |
система, совершающая |
|||||||||||||
колебания, описываемые уравнением вида: |
|
2 |
|
. |
|
|
||||||||||
S |
0 S 0 |
|
|
|||||||||||||
8

§ 4. Свободные затухающие колебания
Колебания, амплитуда которых из-за потерь энергии с течением времени уменьшается, называются свободными затухающими колебаниями.
В механических колебательных системах энергия превращается в теплоту вследствие трения; в электрическом колебательном контуре – это омические потери и излучение электромагнитной энергии.
Дифференциальное уравнение свободных затухающих колебаний:
|
|
|
d 2 S |
2 |
dS |
2 S 0 , |
||||||
|
|
|
|
|
|
|||||||
|
|
|
dt 2 |
|
|
dt |
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||||
где |
S - колеблющаяся величина, |
const |
- коэффициент затухания, 0 - |
|||||||||
циклическая частота свободных |
незатухающих колебаний при 0 или |
|||||||||||
собственная частота колебательной системы. |
|
|
|
|||||||||
|
В случае малых затуханий 2 |
2 |
решение дифференциального уравнения |
|||||||||
|
|
|
|
|
0 |
|
|
|
|
|
||
или уравнение затухающих колебаний: |
|
|
|
|
||||||||
|
|
S Acos( t ) A e t |
cos( t ) |
, |
||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
где - циклическая частота колебаний, |
2 |
02 |
2 |
; |
||||||||
A A e t - амплитуда затухающих колебаний; |
|
|
|
|||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
A0 |
- начальная амплитуда при t 0 . |
|
|
|
|
|
|
|
|
|||
Существуют и другие характеристики затухающих колебаний.
1 - время релаксации, в течении которого амплитуда уменьшается в е раз.
Затухание нарушает периодичность колебаний. Но если затухание мало, то период затухающих колебаний может быть определен по формуле:
|
|
|
|
|
T |
|
2 |
|
|
|
|
|
|
2 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Декремент затухания: |
|
A(t) |
|
|
e T |
- отношение амплитуд, следующих друг |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
A(t T ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
за другом через период. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Логарифмический |
декремент |
затухания: |
|
|
|
ln |
A(t) |
T |
T |
|
1 |
|
- |
|||||||||||||
|
|
|
A(t T ) |
|
Ne |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
логарифм отношения амплитуд, следующих друг за другом через период. |
|
|
|
|
||||||||||||||||||||||
Ne - число колебаний за время уменьшения амплитуды в е раз. |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Добротность: |
Q |
Ne |
|
|
|
|
|
0 |
. Добротность пропорциональна числу |
|||||||||||||||||
T0 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
колебаний Ne , совершаемых системой за время релаксации.
9
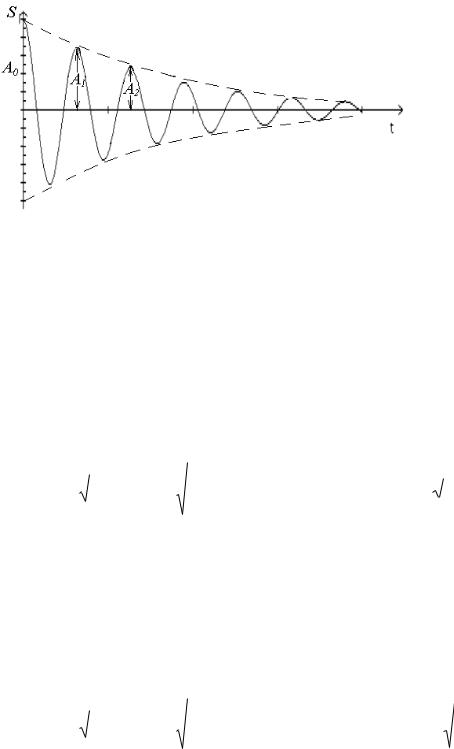
График затухающих колебаний:
Рассмотрим затухающие колебания на примерах пружинного маятника и электрического колебательного контура.
1. Пружинный маятник совершает колебания под действием упругой силы Fупр kx . В реальных условиях на него действует сила трения Fтр rV rx ,
где к – коэффициент сопротивления среды. Сила трения противоположно направлена вектору скорости, отсюда знак минус «-». Закон движения маятника:
mx kx rx ; x |
r |
x |
k |
x 0 . Введем обозначение: |
r |
2 , |
k |
2 . |
|
|
|
|
|||||
|
m |
|
m |
m |
m |
0 |
||
|
|
|
||||||
Дифференциальное уравнение затухающих колебаний маятника: x 2 x 02 x 0 .
Уравнение колебаний: |
x A e t cos( t ) . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
r 2 |
|
|
1 |
|
|
|
|
|
|
Циклическая частота: |
2 |
2 |
|
|
|
; добротность: Q |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
km . |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
m |
|
|
|
4m2 |
|
|
r |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2. Электрический колебательный контур. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
R 0 |
; IR U |
|
|
|
; U |
|
|
q |
; |
|
|
L |
dI |
. Подставим в уравнение: Lq Rq |
q |
0 ; |
|||||||||||||||||||||
C |
S |
C |
|
|
S |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
C |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
q |
R |
q |
1 |
q 0 . Обозначим: |
|
1 |
|
2 |
, |
|
|
R |
2 . |
|
|
|
|
|
|||||||||||||||||||
|
L |
|
LC |
|
|
|
|
|
|
|
|
|
|
|
LC |
0 |
|
|
|
|
L |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Дифференциальное уравнение затухающих колебаний контура: q 2 q 02 q 0 .
Уравнение колебаний: q q |
max |
e t cos( t ) . |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; добротность: Q |
1 |
|
|
L |
. |
||||
Циклическая частота: |
2 |
2 |
|||||||||||||||
|
|
|
|
|
|||||||||||||
|
|
0 |
|
|
|
LC |
|
4L2 |
|
|
R |
|
|
C |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||
§ 5. Вынужденные колебания
Чтобы в реальной колебательной системе получить незатухающие колебания, надо компенсировать потери энергии. Это возможно с помощью периодически
действующего фактора: X (t) X 0 cos t . |
|
|
При механических колебаниях – это |
внешняя |
вынуждающая сила: |
F F0 cos t , при электрических колебаниях – |
внешняя |
ЭДС или переменное |
напряжение: U U max cos t .
Колебания, возникающие под действием внешнего периодически действующего фактора, называются вынужденными.
10
