Лекция 3. П.3. Отношения на множествах. Свойства бинарных отношений.

3.1. Бинарные отношения.

Когда говорят о родстве двух людей, например, Сергей и Анна, то подразумевают, что есть некая семья, к членам которой они относятся. Упорядоченная пара (Сергей, Анна) отличается от других упорядоченных пар людей тем, что между Сергеем и Анной есть некое родство (кузина, отец и т.д.).

В математике среди всех упорядоченных пар прямого произведения двух множеств A и B (AB) тоже выделяются «особые» пары в связи с тем, что между их компонентами есть некоторые «родственные» отношения, которых нет у других. В качестве примера рассмотрим множество S студентов какого-нибудь университета и множество K читаемых там курсов. В прямом произведении SK можно выделить большое подмножество упорядоченных пар (s, k), обладающих свойством: студент s слушает курс k. Построенное подмножество отражает отношение «… слушает …», естественно возникающее между множествами студентов и курсов.

Для строгого математического описания любых связей между элементами двух множеств введем понятие бинарного отношения.

Определение 3.1. Бинарным (или двухместным) отношением  между множествами A и B называется произвольное подмножество AB, т.е.

.

В частности, если A=B (то есть A²), то говорят, что  есть отношение на множестве A.

Элементы a и b называются компонентами (или координатами) отношения .

Замечание. Договоримся, что для обозначения отношений между элементами множеств использовать греческий алфавит: , , , ,  и т.д.

Определение 3.2. Областью определения бинарного отношения  называется множество D_=a   b, что ab (левая часть). Областью значений бинарного отношения  называется множество R_=b   a, что ab (правая часть).

Пример .. Пусть даны два множества A=1; 3; 5; 7 и B=2; 4; 6. Отношение зададим следующим образом =(x; y)AB  x+y=9. Это отношение будет состоять из следующих пар (3; 6), (5; 4) и (7; 2), которые можно записать в виде =(3; 6), (5; 4), (7;2). В данном примере D_=3; 5; 7 и R_= B=2; 4; 6.



Пример .. Отношение равенства на множестве действительных чисел есть множество =(x; y)  x и y – действительные числа и x равно y. Для этого отношения существует специальное обозначение «=». Область определения совпадает с областью значений и является множеством действительных чисел, D_= R_.



Пример .. Пусть A – множество товаров в магазине, а B – множество действительных чисел. Тогда =(x; y)AB  y – цена x – отношение множеств A и B.



Если обратить внимание на пример 3.1., то можно заметить, что данное отношение было задано сначала в виде =(x; y)AB  x+y=9, а потом записано в виде =(3; 6), (5;4), (7;2). Это говорит о том, что отношения на множествах (или одном множестве) можно задавать различными способами. Рассмотрим способы задания бинарных отношений.

Способы задания отношений:

1) с помощью подходящего предиката;

2) множество упорядоченных пар;

3) в графической форме: пусть A и B – два конечных множества и  – бинарное отношение между ними. Элементы этих множеств изображаем точками на плоскости. Для каждой упорядоченной пары отношения  рисуют стрелку, соединяющую точки, представляющие компоненты пары. Такой объект называется ориентированным графом или орграфом, точки же, изображающие элементы множеств, принято называть вершинами графа.

4) в виде матрицы: пусть A=a₁, a₂, …, a_n и B=b₁, b₂, …, b_m,  – отношение на AB. Матричным представлением  называется матрица M=m_ij размера nm, определенная соотношениями

.

Кстати, матричное представление является представлением отношения в компьютере.

Пример .. Пусть даны два множества A=1; 3; 5; 7и B=2; 4; 6. Отношение задано следующим образом =(x; y)  x+y=9. Задать данное отношение как множество упорядоченных пар, орграфом, в виде матрицы.

Решение. 1) =(3; 6), (5; 4), (7; 2) - есть задание отношения как множества упорядоченных пар;

2) соответствующий ориентированный граф показан на рисунке.

3) в матричном представлении это отношение имеет вид

. 

Пример .. Еще в качестве примера можно рассмотреть предложенную Дж. фон Нейманом (1903 – 1957) блок-схему ЭВМ последовательного действия, которая состоит из множества устройств M:

,

где a – устройство ввода, b – арифметическое устройство (процессор), c – устройство управления, d – запоминающее устройство, e – устройство вывода.

Рассмотрим информационный обмен между устройствами m_i и m_j, которые находятся в отношении , если из устройства m_i поступает информация в устройство m_j.

Это бинарное отношение можно задать перечислением всех его 14 упорядоченных пар элементов:

Соответствующий орграф, задающий это бинарное отношение, представлен на рисунке:

Матричное представление этого бинарного отношения имеет вид:

. 

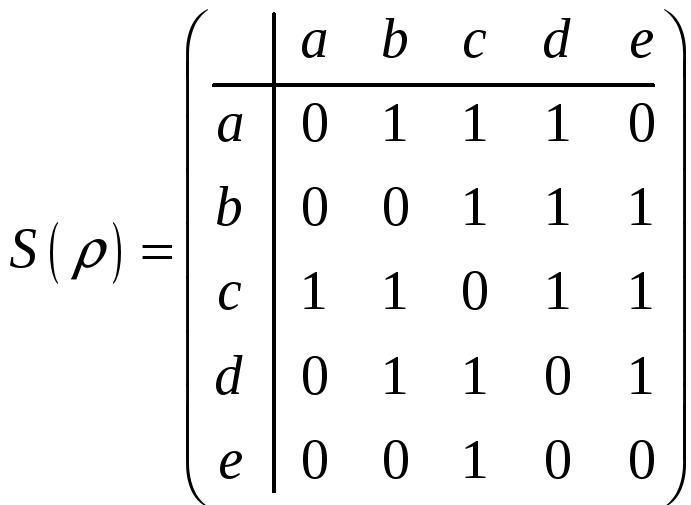Для бинарных отношений обычным образом определены теоретико-множественные операции: объединение, пересечение и т.д.

Введем обобщенное понятие отношения.

Определение 3.3. n-местное (n-арное) отношение  – это подмножество прямого произведения n множеств, то есть множество упорядоченных наборов (кортежей)

A₁…A_n=(a₁, …, a_n) a₁A₁ … a_nA_n

Многоместные отношения удобно задавать с помощью реляционных таблиц. Такое задание соответствует перечислению множества n-к отношения . Реляционные таблицы широко используются в компьютерной практике в реляционных базах данных. Заметим, что реляционные таблицы нашли применение в повседневной практике. Всевозможные производственные, финансовые, научные и другие отчеты часто имеют форму реляционных таблиц.

Слово «реляционная» происходит от латинского слова relation, которое в переводе на русский язык означает «отношение». Поэтому в литературе для обозначения отношения используют букву R (латинскую) или  (греческую).

Далее мы будем рассматривать только двухместные (бинарные) отношения, при этом опуская слово «бинарные».

Определение 3.4. Пусть AB есть отношение на AB. Тогда отношение ^-1 называется обратным отношением к данному отношению  на AB, которое определяется следующим образом:

^-1=(b, a)  (a, b).

Определение 3.5. Пусть  AB есть отношение на AB, а  BC – отношение на BC. Композицией отношений  и  называется отношение  AC,которое определяется следующим образом:

=◦= (a, c)  b  B, что (a, b) и (b, c).

Пример .. Пусть , и C=, , , . И пусть отношение  на AB и отношение  на BC заданы в виде:

=(1, x), (1, y), (3, x);

=(x, ), (x, ), (y, ), (y, ).

Найти ^-1 и ◦, ◦.

Решение. 1) По определению ^-1=(x, 1), (y, 1), (x, 3);

2) Используя определение композиции двух отношений, получаем

◦=(1, ), (1, ), (1, ), (1, ), (3, ), (3, ),

поскольку из (1, x) и (x, ) следует (1, )◦;

из (1, x) и (x, ) следует (1, )◦;

из (1, y) и (y, ) следует (1, )◦;

…

из (3, x) и (x, ) следует (3, )◦.

3) ◦=.



Теорема 3.1. Для любых бинарных отношений выполняются следующие свойства:

1) ;

2) ;

3) - ассоциативность композиции.

Доказательство. Свойство 1 очевидно.

Докажем свойство 2. Для доказательства второго свойства покажем, что множества, записанные в левой и правой частях равенства, состоят из одних и тех же элементов. Пусть (a; b)  (◦)^-1  (b; a)  ◦   c такое, что (b; c)   и (c; a)     c такое, что (c; b)  ^-1 и (a; c)  ^-1  (a; b)   ^-1◦ ^-1.

Свойство 3 доказать самостоятельно.

■