Лекция 8. П.8. Деревья. Остовные деревья.

8.1. Деревья.

Существует один простой и важный тип графов, которому разные авторы дали одинаковое название – деревья. Для них выполняются многие интересные утверждения, которые не всегда выполняются для графов в общем случае. Деревья являются самым распространенным классом графов, применяемых в программировании, причем в самых разных ситуациях.

Определение 8.1.Деревом называется графT(V,E) без циклов.Лес– это граф, компоненты которого являются деревьями.

Ориентированное дерево Tпредставляет собой свободный от петель ориентированный граф, соотнесенный граф которого является деревом.

Если дерево имеет хотя бы одно ребро, оно имеет хотя бы две вершины со степенью 1. Вершины степени 1 называются листьями. Другие вершины называютсявнутренними вершинами.

Если дерево изображено таким образом, что в верхней части помещена вершина, а остальные находятся ниже его, то вершина в самой верхней части называется корнемдерева. Если корень дерева определен, то дерево называетсякорневым деревом.

Если корень выбран, уровень вершины vопределяется длиной единственной цепи из корня в вершинуv.

Определение 8.2.Высотой дерева называется длина самой длинной цепи от корня до листа. Высоту дерева будем обозначатьh(T).

Пример 8.1.



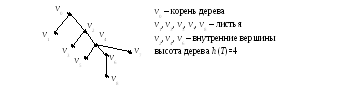
Примеры изображения деревьев в программировании.

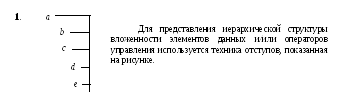
Тот факт, что большинство систем управления файлами использует ориенти-рованные деревья, отражается даже в терминологии – «корневой каталог диска».

Генеалогическое дерево семейства Бернулли.

Купеческая протестантская семья Бернулли жила в Антверпене (Нидерланды). Свой род она вела из Фландрии, где Бернулли, в XV в. носили еще фамилию Бернуйла (Bernuilla). В связи с событиями XVI в. на территории Нидерландов, что направленные были против протестантов, семья Бернулли была вынуждена уехать во Франкфурт-на-Майне. В это время главой семьи был Якоб Бернулли, который умер в 1583 г.

Среди Бернулли некоторые имена повторялись из поколения в поколение, поэтому их различают, как королей, присоединив к имени соответствующую цифру. В виде дерева показана родословная семейства Бернулли.

Якоб I (1654-1705) – швейцарский математик. По образованию богослов. С 1687 г. профессор математики Базельского университета. Ему принадлежат важные заслуги в развитии анализа бесконечно малых, начало которому положила работа Лейбница, опубликованная в 1684 г. Он вычислил площади многих плоских фигур, площади поверхностей и длины линий. Другие работы относятся к алгебре, арифметике, геометрии, теории рядов, теории вероятностей, а также к физике. В книге «Искусство предположений» доказал теорему (названную позже его именем), имеющую важное значение в теории вероятностей и ее приложениях к статистике. Учениками Якоба I были: его младший брат Иоганн I, племянник Николай I, член Петербургской академии наук, механик и математик Я. Герман, отец великого Л. Эйлера — Пауль Эйлер.

Иоганн I (1667-1748). Брат Якоба I. Десятый ребенок в семье Николая. По образованию врач. С 1695 г. профессор математики Гронингенского университета (Голландия). С 1705 г. профессор математики Базельского университета. Почетный член Петербургской академии наук.

Николай I (1687-1759) – швейцарский математик, сын Николая. По образованию юрист. Был профессором математики в Падуе, а затем профессором логики и права в Базельском университете. Его исследования посвящены теории вероятностей, интегральному исчислению, демографии.

Николай II (1695-1726), сын Иоганна I. По образованию юрист. Профессор права в Берне, профессор математики в Петербурге.

Даниил I (1700-1782). Уроженец Гронингена, сын Иоганна I. По образованию врач. В 1725-1733 гг. работал на кафедрах физиологии и механики в Петербургской академии наук. С 1733 г. профессор по кафедре физиологии, с 1750 г. профессор по кафедре механики в Базеле. Почетный член Петербургской академии наук. В математике Даниилу Бернулли принадлежат: метод численного решения алгебраических уравнений с помощью возвратных рядов, работы по обыкновенным дифференциальным уравнениям, по теории вероятностей с приложением к статистике народонаселения и отчасти у астрономии, по теории рядов. В работах, завершенных написанным в Петербурге трудом «Гидродинамика» (1738), вывел основное уравнение стационарного движения идеальной жидкости, носящее его имя. Разрабатывал кинематические представления о газах.

Иоганн II (1710-1790), сын Иоганна I. По образованию юрист. Профессор элоквенции (красноречия), профессор математики в Базеле.

Иоганн III (1744-1807), старший сын Иоганна II. По образованию юрист. Астроном Берлинской академии наук, там же директор математического класса.

Даниил II (1751-1834), второй сын Иоганна II. По образованию врач, профессор красноречия в Базеле.

Якоб II (1759-1789), третий сын Иоганна II. По образованию юрист. Математик Петербургской академии наук.

Кристоф (1782-1863), сын Даниила II. Профессор технологии в Базеле.

Иоганн-Густав (1811-1863), сын Кристофа. Профессор технологии в Базеле.

Представители рода Бернулли живут в Базеле и в настоящее время.

Рассмотрим некоторые утверждения, которые относятся к деревьям.

Теорема 8.1.Для любых вершинaиbдереваTсуществует единственная цепь изaвb.

Доказательство.Доказательство проведем методом «от противного». Предпо-ложим, что для некоторых вершинaиbдереваTцепь изaиbне является единственной, и покажем, что в таком случаеTне будет деревом.

На основании следующей теоремы можно убедиться в том, что верна также и обратная теорема, которую мы примем без доказательства.

Теорема 8.2.Если для любых двух вершин графаGсуществует единственная цепь из вершиныaв вершинуb, тогдаGявляется деревом.

Теорема 8.3.Если у дереваTимеетсяeребер иvвершин, тоv=e+1.

Доказательство.Предположим, что имеется деревоT. Любое дерево можно представить как корневое дерево, и это никаким образом не меняет ни числа ребер, ни числа вершин.

Рассмотрим теперь ориентированное дерево T, порожденное деревомT. У каждой дуги ориентированного дерева одна и только одна конечная вершина. Следовательно, число дуг и вершин одно и то же, исключая корневую. Если учесть корневую вершину, получим, что вершин на одну больше, чем дуг.

Значит, и исходное дерево имеет число вершин на одну больше, чем число ребер.

■

Справедлива также и обратная теорема, которую примем без доказательства.

Теорема 8.4.Если в связном графеG, содержащемeребер иvвершин и имеемv=e+1, тоGявляется деревом.