8.3. Алгоритм Краскала и алгоритм Прима.

В предыдущей лекции мы ввели понятие взвешенного графа, как графа, каждому ребру которого приписано положительное число, называемое весом. Этот вес может описывать расстояние, стоимость или другие данные.

Определение 8.5.Вес остовного дерева взвешенного графаGравен сумме весов, приписанных ребрам остовного дерева. Будем обозначать(T).

Минимальным остовным деревомназывается такое остовное дерево графаG, что весTменьше или равен весу любого другого остовного дерева графаG. Вес минимального остовного дерева будем обозначать_min(T).

Построение остова графа G, имеющего наименьший вес, имеет широкое применение при решении некоторого класса задач прикладного характера. Дадим формулировку одной из таких задач.

Формулировка задачи:Пусть, например,G=(V,E,) служит моделью железнодорожной сети, соединяющей пунктыv₁,v₂, …,v_nV, а(v_i,v_j) – расстояние между пунктамиv_iиv_j. Требуется проложить сеть телеграфных линий вдоль железнодорожной сети так, чтобы все пунктыv₁,v₂, …,v_nбыли связаны между собой телеграфной сетью, протяженность которой была бы наименьшей.

Мы рассмотрим два способа построения минимального остовного дерева взве-шенного графа: алгоритм Краскала и алгоритм Прима.

Первым рассмотрим алгоритм Краскала. Идея метода состоит в том, чтобы формировать дерево T(V,E), выбирая ребра с наименьшим весом так, чтобы не возникал цикл.

Алгоритм Краскала:

1) Выбрать в графе Gреброeминимального веса, не принадлежащее множествуEи такое, что его добавление вEне создает цикл в деревеT.

2) Добавить это ребро во множество ребер E.

3) Продолжить, пока имеются ребра, обладающие указанными свойствами.

Вторым рассмотрим алгоритм Прима. Принципиальное отличие алгоритма состоит в том, что всегда имеется дерево, к которому ребра добавляют до тех пор, пока не получится остовное дерево.

Алгоритм Прима:

1) Выбрать вершину v₀графаGи ребро с наименьшим весомe₁, для которогоv₀– одна из вершин, и сформировать деревоT₁.

2) Для заданного дерева T_kс ребрамиe₁,e₂,e₃, …,e_k, если имеется вершина, не принадлежащаяT_k, выбрать ребро с наименьшим весом, смежное с ребром дереваT_kи имеющее вершину вне дереваT_k. Добавить в деревоT_k, формируя деревоT_k+1.

3) Продолжить, пока имеются вершины графа G, не принадлежащие дереву.

Построение минимального оствного дерева можно проводить двумя способами: 1) остов графа строится непосредственно на самом графе, выделяя ребра утолщенной линией, которые входят в остовное дерево; 2) строится отдельно корневое дерево, которое будет минимальным остовным деревом. Второй случай используется, если требуется определить высоту построенного дерева.

Пример 8.3.Для данного взвешенного графа:

1) определить степень каждой вершины;

2) построить матрицу смежности вершин, матрицу смежности ребер, матрицу инциденций;

3) найти число остовных деревьев, используя теорему Кирхгофа;

4) найти минимальное корневое остовное дерево, используя алгоритм Краскала или алгоритм Прима. Определить высоту построенного дерева.

Решение.1) Используя определение степени вершины графа, находим:

d(v₁)=3,d(v₂)=3,d(v₃)=4,d(v₄)=3,d(v₅)=2,d(v₆)=3.

2) Построим матрицу смежности вершин. Данный граф имеет шесть вершин, поэтому матрица смежности вершин является квадратной матрицей шестого порядка. Для заполнения первой строки матрицынайдем число ребер, соединяющих первую вершину с каждой из остальных вершин.

Поскольку количество ребер, соединяющих первую вершину с первой равно 0 (в графе нет петель, соответствующих первой вершине), соединяющих первую со второй равно 1, первую с третьей равно 1, первую с четвертой равно 1, первую с пятой равно 0, первую с шестой равно 0, то первая строка матрицы имеет вид (0 1 1 1 0 0). Заполняя аналогично остальные строки, получаем матрицувида:

.

Для построения матрицы смежности ребер и матрицы инциденций рассмотрим не взвешенный граф, предварительно занумеровав ребра графа произвольным образом.

Так как граф имеет девять ребер, то матрица смежности ребер является квадратной матрицей девятого порядка. Реброu₁имеет общую вершину с ребрамиu₃иu₅, а также общую вершину с ребрамиu₂иu₄. Поэтому первая строка матрицыимеет вид (0 1 1 1 1 0 0 0 0). Заполняем аналогично остальные строки, получаем матрицувида:

.

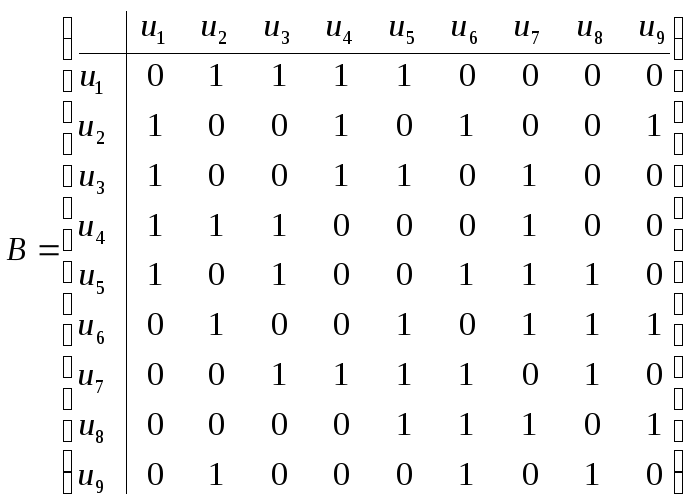Граф имеет шесть вершин и девять ребер, поэтому матрица инциденций является матрицей размерности 69. Поскольку вершинаинцидентна ребрам,и, и не инцидентна остальным ребрам, то первая строка матрицыимеет вид (0 0 1 1 0 0 1 0 0). Остальные строки матрицы заполняем аналогично. Следовательно, матрицаимеет вид:

.

3) Для того, чтобы найти число остовных деревьев, сначала составим матрицу Кирхгофа.

.

Используя теорему Кирхгофа, найдем, например, алгебраическое дополнение элемента .

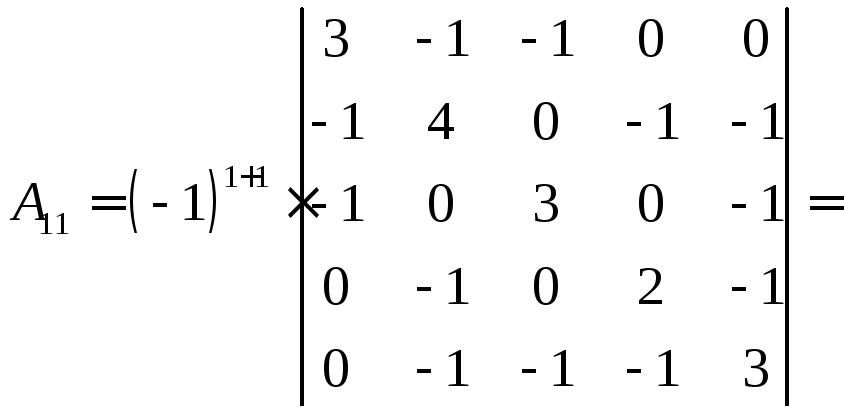
=четвертую и пятую строчки оставляем,

третью умножаем на (1) и складываем со второй,

потом третью умножаем на 3 и складываем с первой=

.

Таким образом, для данного графа можно построить 64 остовного дерева.

4) Для построения минимального остовного (корневого) дерева рассмотрим взвешенный граф, данный в условии задачи.

Используем для построения остовного дерева алгоритм В графе выбираем ребро с минимальным весом. В нашем случае это ребро, соединяющее вершины ис весом, равным 4. Пусть, например, вершинабудет корнем дерева. Далее выбираем ребра, инцидентные вершинам,и имеющие минимальный вес. Таким является ребро с весом 5, соединяющее вершиныи. Включаем его в строящееся дерево. Затем к вершинеприсоединяем ребро с весом 7, соединяющее вершиныи. К вершинеприсоединяем ребро с весом 7, соединяющее вершиныи. И в заключение, к вершинеприсоединяем ребро с весом 6, соединяющее вершиныи. Таким образом, получаем минимальное остовное дерево (рис. 1). Минимальный вес построенного дерева равен:_min(T)=4+5+7+7+6=29.

Так как мы в качестве корня дерева выбрали вершину , то высота дерева будет равнаh(T)=4.

Замечание.Если бы в качестве корня выбрали вершину, то высота дерева была бы равнаh(T)=5.

ИЛИ

Построим минимальное корневое остовное дерево данного взвешенного графа с помощью алгоритма Прима. Выбираем вершину , которая будет корнем дерева. Из трех ребер, которые инцидентны вершине, выбираем те, что имеют наименьший вес. Два ребра с весом, равным 7, инцидентны вершине. Присоединяем эти ребра к выбранной вершине. К вершинеприсоединяем ребро с весом 5, соединяющее вершиныи. К вершинеприсоединяем ребро с весом 4, соединяющее вершиныи. К вершинеприсоединяем ребро с весом 6, соединяющее вершиныи.Таким образом, получаем следующее минимальное корневое дерево с весом, равным_min(T)=7+7+6+5+4=29. Высота построенного дерева равнаh(T)=3.

Ответ.1)d(v₁)=3,d(v₂)=3,d(v₃)=4,d(v₄)=3,d(v₅)=2,d(v₆)=3;

3) число остовных деревьев равно 64;

4) минимальный вес дерева равен _min(T)=29, высота равнаh(T)=4.