
- •Дать определение частоты появления события и сформулировать аксиому измерений.
- •Записать формулу полной вероятности и формулу Байеса.
- •Сформулировать закон больших чисел и теорему Бернулли.
- •Сформулировать условия, при которых распределение пуассоновского импульсного процесса близко к нормальному.
- •Сформулировать теорему Кемпбелла для пуассоновского импульсного процесса.
- •Дать определения непрерывности, дифференцируемости, интегрируемости и стационарности случайной функции.
- •Записать уравнение фпк, пояснить смысл его коэффициентов и привести условия, при котором оно существует.
-
Сформулировать условия, при которых распределение пуассоновского импульсного процесса близко к нормальному.
![]() -пуассоновский
процесс нормальный, когда семииварианты
характеристической функции начиная с
m=3 малы.
-пуассоновский
процесс нормальный, когда семииварианты
характеристической функции начиная с
m=3 малы.
![]()
-
Сформулировать теорему Кемпбелла для пуассоновского импульсного процесса.
Если импульсы имеют одинаковую высоту, то есть i = a, на основе выражения для первого моменты и дисперсии (см. ниже)
![]()
получим:
![]() .
.
Эта пара соотношений называется теоремой Кэмпбелла.
-
Дать определения непрерывности, дифференцируемости, интегрируемости и стационарности случайной функции.
Случайная функция называется непрерывной в среднеквадратичном смысле, если
![]() .
.
Этот предел часто обозначают следующим образом:
![]() .
.
Случайная функция называется непрерывной по вероятности, если ее среднее арифметическое сходится к математическому ожиданию в каждый момент времени:
![]() .
.
Наконец, случайная функция называется непрерывной почти наверняка, если
![]() .
.
Существует сокращенное обозначение этого равенства:
![]() .
.
Дифференцируемость случайной функции – существование в каком-либо смысле предела приращения функции к приращению аргумента
![]() .
.
Интегрируемость случайной функции определяется как существование в каком-либо смысле предела частичных сумм
 .
.
-
Дать определение коэффициента корреляции случайной функции.
 -
коэффициент корреляции.
-
коэффициент корреляции.
-
Дать определение среднего по времени и записать условие Слуцкого для эргодичности случайного процесса.
![]() -
среднее по
времени,
которое, в свою
очередь, также является случайной
величиной.
-
среднее по
времени,
которое, в свою
очередь, также является случайной
величиной.
 -
условием эргодичности Слуцкого
для стационарных случайных процессов.
-
условием эргодичности Слуцкого
для стационарных случайных процессов.
-
Доказать, что функция автокорреляции стационарного случайного процесса ограничена по модулю.
Представим функцию автокорреляции в показательной форме B(t1,t2) = |B(t1,t2)|exp{(t1,t2)} и рассмотрим при произвольном a величину

Поскольку среднее от квадрата модуля любой величины неотрицательно, а |cos( – a)| 1,
получаем
![]() ,
,
то есть функция автокорреляции ограничена по модулю. Очевидно, для стационарного случайного процесса |B()| <|(t)|2> = B(0).
-
Сформулировать соотношение неопределенностей и привести минимизирующие его функции.
![]() -
соотношение
неопределенностей.
Доказано, что равенство в выражении
реализуется только для гауссовых функции
корреляции и спектральной плотности
интенсивности:
-
соотношение
неопределенностей.
Доказано, что равенство в выражении
реализуется только для гауссовых функции
корреляции и спектральной плотности
интенсивности:
![]() ,
,
![]() ,
а следовательно гауссовы кривые такого
вида
являются
минимизирующими.
,
а следовательно гауссовы кривые такого
вида
являются
минимизирующими.
G(i) называется спектральной плотностью интенсивности случайного процесса. Функция автокорреляции В().
-
Дать определение белого шума и привести его функцию автокорреляции и спектральную плотность интенсивности.
Случайный процесс, спектральная плотность интенсивности которого постоянна G(j) = G0, называется белым шумом.
 -
спектральная
плотность интенсивности
на частотах
<< 1/0.
-
спектральная
плотность интенсивности
на частотах
<< 1/0.
Белый шум во всем
частотном диапазоне G(j)
= G0,
которому соответствует автокорреляционная
функция-
![]() .
По этой причине белый шум часто называют
дельта-коррелированным процессом.
.
По этой причине белый шум часто называют
дельта-коррелированным процессом.
-
Записать спектральную плотность интенсивности процесса на выходе линейной системы, на вход которой воздействует случайный процесс.
![]()
![]() -
спектральную плотность интенсивности
процесса на выходе линейной системы.
-
спектральную плотность интенсивности
процесса на выходе линейной системы.
-
Сформулировать теорему о нормализации.
Выберем временной интервал так, чтобы выполнялось условие 1 << << р и перепишем интеграл Дюамеля в виде

где
![]() ,
,
![]() ,
N
= р/
>> 1. Поскольку
>> 1,
можно считать, что величины n
некоррелированы, а выходной процесс
2(t)
является суммой большого числа
некоррелированных случайных величин;
тогда в силу центральной предельной
теоремы он является нормальным процессом.
Таким образом, при прохождении через
узкополосную систему любой стационарный
случайный процесс нормализуется – в
этом состоит суть так называемой теоремы
о нормализации.
,
N
= р/
>> 1. Поскольку
>> 1,
можно считать, что величины n
некоррелированы, а выходной процесс
2(t)
является суммой большого числа
некоррелированных случайных величин;
тогда в силу центральной предельной
теоремы он является нормальным процессом.
Таким образом, при прохождении через
узкополосную систему любой стационарный
случайный процесс нормализуется – в
этом состоит суть так называемой теоремы
о нормализации.
-
Записать выражение для спектра колебаний с флуктуирующей частотой и привести формулы для случаев, когда наблюдаются медленные и большие или малые и быстрые флуктуации частоты.

 -
медленные и большие флуктуации частоты.
-
медленные и большие флуктуации частоты.
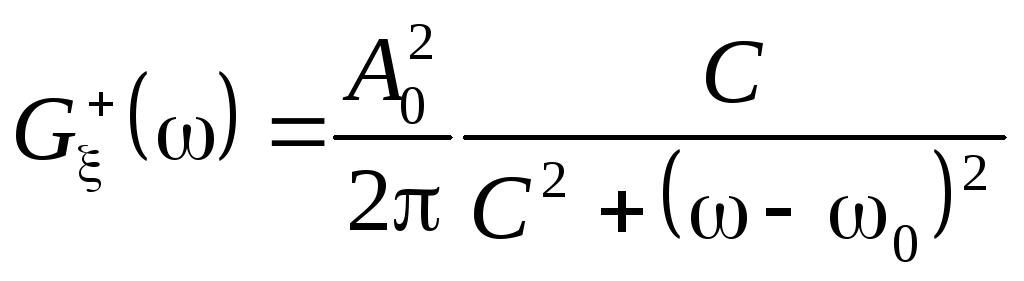 -малые
и быстрые флуктуации частоты.
-малые
и быстрые флуктуации частоты.
-
Записать выражения для смещенной и несмещенной оценок автокорреляционной последовательности.
![]() -
несмещенная
оценка АКП.
-
несмещенная
оценка АКП.
![]() -
смещенная оценка
АКП.
-
смещенная оценка
АКП.
-
Записать выражения для периодограмм Даньелла и Уэлча.
При усреднении выборочного спектра по соседним частотам получим периодограмму Даньелла:
![]() .
.
Полный вид периодограммы Уэлча записывается как среднее значение периодограмм сегментов:
![]() .
.
-
Дать определение Марковского процесса и получить уравнение Смолуховского.
Случайные процессы, функции плотности вероятности которых удовлетворяют соотношению:
![]()
называют марковскими процессами первого порядка.
Применяя выражение последовательно n раз, получим
![]()
Таким образом, для полного задания функции n марковского процесса необходимо знать только две функции плотности вероятности – n(t1, x1) и (tn, xn| tn–1, xn–1). Условная функция распределения (tn, xn| tn–1, xn–1) называется вероятностью перехода из состояния tn–1, xn–1 в состояние tn, xn.
![]() -
уравнение
Смолуховского.
-
уравнение
Смолуховского.
