И.А. Паначев Рабочая программа, контрольные работы и методические указания по их выполнению для студентов заочной формы обучения (сокращенные сроки обучения на базе среднего спец. образования)

50

Рис.11.4. Схема балки (а), эпюра Q (б), и эпюра М (в)

Проверка:

∑Y = 0,

Ya +Yв − 2q1a − 2P2 − P1 = 0, 27,5 + 62,5 −10 2 − 40 −30 = 0.

Следовательно, реакции опор определены правильно.

Б. Разбиваем балку на характерные участки и составляем уравнения Q и М для каждого участка, используя формулы (11.1) и (11.2).

Первый участок 0 ≤ Z1 ≤ 2 (рис.11.4,а)

Q(z1) =Ya −2q1z1,

51

Третий участок 4 ≤ Z3 ≤ 6 (рис.11.4,а)

Вданном случае целесообразнее при составлении уравнений Q(z3)

иМ(z3) взять все внешние силы с правой стороны от рассматриваемого

В. Для определения знаков слагаемых, входящих в выражения для М(z), удобно использовать следующий приём:

-мысленно представить отсечённую часть (здесь и далее левую) в виде консоли с заделкой в месте проведения сечения;

-приложить нагрузку и проанализировать характер изгиба консоли от неё, выяснить, какие волокна в сечении (заделка) растягиваются;

52

- присвоить знак слагаемого, учитывающего эту нагрузку, в соответствии с принятым правилом знаков.

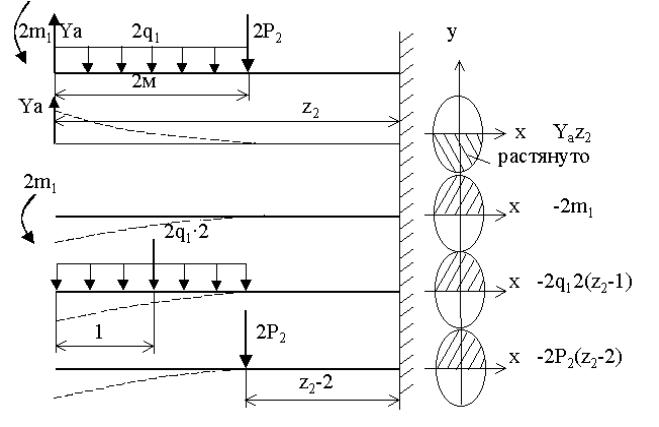
Этот приём для второго участка проиллюстрируем на рис. 11.5. Эпюры Q и М, построенные по значениям табл. 11.1, 11.2 и 11.3,

показаны на рис. 11.4,б,в.

Г. Подбор сечения. Определяем опасное сечение и M max , используя построенную эпюру М:

M max = 60 кН.м ( см. рис. 11.4,в).

Определяем расчётный момент сопротивления сечения изгибу

Д. Для ускорения построения эпюр можно использовать способ “характерных сечений”. Характерными считаются сечения, ограничивающие участок балки. Суть способа состоит в том, что величины Q и М находятся только в этих сечениях, и для дальнейшего построения этих эпюр используют правила контроля эпюр, основанные на дифференциальных зависимостях (11.4).

11.6.2. Схема б. Для балки, приведённой на рис. 11.3,б, построить эпюры Q и М методом характерных сечений, если дано:

Р1 = 10 кН, q2 = =20 кН/м, q3 = 2 кН/м,

а = 2 м.

53

Рис. 11.5. Схема определения знаков отдельных видов нагрузки

Решение.

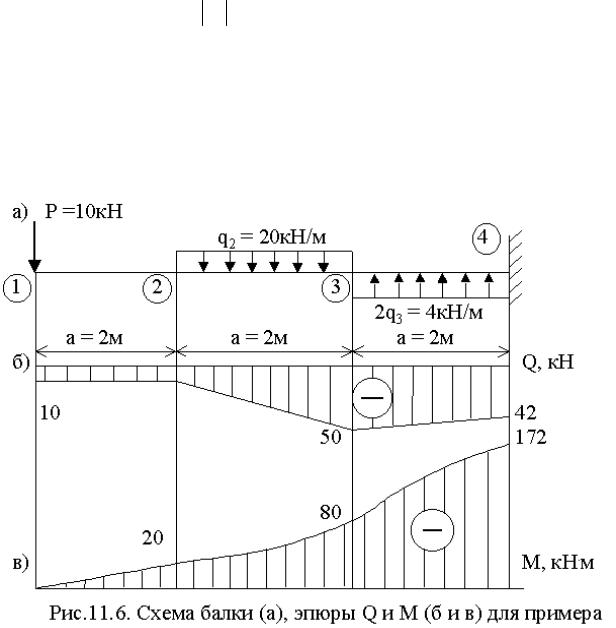
А. Для консольной балки нет необходимости определять опорные реакции, так как двигаясь со стороны консоли, мы будем знать все силы с одной стороны от сечения (рис. 11.6,а).

Б. Для построения эпюр Q и М используем метод характерных сечений:

Q1 = -P1 = -10 кН,

Q2 = -P1 = -10 кН,

Q3 = -P1 – q2·2 = -10 – 20·2 = -50 кН,

Q4 = -P1 – q2·2 + 2·q3·2 = -10 – 20·2 + 2·2·2 = -42 кН.

Эпюра Q показана на рис. 11.6,б.

М1 = 0,

М2 = -Р1·La = -10·2 = -20 кНм,

М3 = -Р1·2·а – q2·a2/2 = -10·2·2 – 20·22/2 = -80 кН.м, М4 = -Р1·3·а – q2·a·1,5·a + 2·q3·a2/2 =

= -10·3·2 – 20·2·1,5·2 + 2·2·22/2 =172 кН.м.

54

Эпюра М показана на рис. 11.6,в.

В. Подбор сечения

M max = 172 кН.м, см. рис.11.6,в,

11.7. Правила контроля эпюр Q и М

(правила сформулированы для построения эпюр слева направо) 11.7.1. Если на границе участка приложена сосредоточенная сила,

то:

а) на эпюре Q в данном сечении должен быть скачок на величину данной силы в направлении её действия;

б) на эпюре М в данном сечении будет излом, остриём направленный в сторону, противоположную действию силы (если эпюры строятся на сжатом волокне).

55

11.7.2.Если на участке не действует равномерно распределённая нагрузка q = 0, то:

а) эпюра Q представляет собой прямую, параллельную базовой линии;

б) эпюра М представляет собой прямую, наклонную к базовой линии.

11.7.3.Если на участке действует равномерно распределённая нагрузка q ≠ 0, то:

а) эпюра Q представляет собой прямую, наклонную к базовой линии, причём если q направлена сверху вниз, то Q убывает и наоборот;

б) эпюра М представляет собой кривую второго порядка (парабола), выпуклостью направленную в сторону действия q.

11.7.4.Если в каком-либо сечении на участке Q равна 0, то на эпюре М в этом сечении будет экстремум, причём если Q меняет знак с (+) на ( - ) , то это максимум и наоборот.

11.7.5.Если на границе участка приложен сосредоточенный момент, то на эпюре М в данном сечении будет скачок на величину этого момента.

11.7.6.Если на участке Q > 0, то и М > 0 (положительная ордината возрастает, отрицательная убывает), если Q < 0, то и М < 0 (положительная ордината убывает, отрицательная возрастает).

11.7.7.Если крайняя опора или конец консоли не загружены моментом от пары сил, то изгибающий момент в данных сечениях равен нулю.

11.7.8.Если крайняя опора или конец консоли загружены моментом от пары сил, то изгибающий момент в данных сечениях равен по величине этому моменту.

12.ВНЕЦЕНТРЕННОЕ СЖАТИЕ (РАСТЯЖЕНИЕ) ПРЯМОГО БРУСА

Пусть продольная нагрузка приложена не в центре тяжести поперечного сечения стержня, а с некоторым смещением (эксцентриситетом) относительно главных осей сечения (рис.12.1,а).

Для определения внутренних усилий, возникающих в сечении бруса при внецентренном сжатии (растяжении), вначале мысленно перенесём силу Р параллельно самой себе в центр тяжести сечения (начало координат).Возникающий при таком переносе момент пары сил разложим на два составляющих момента: МХ = -РyP и МY = -РхР (рис.12.1,б).

56

Таким образом, действие силы Р, приложенной к сечению внецентренно, эквивалентно совместному действию центрально приложенной силы Р и двух внешних сосредоточенных моментов МХ и МY.

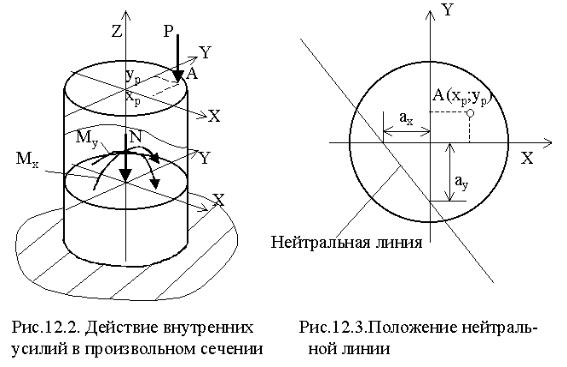
Пользуясь методом сечений, нетрудно установить, что во всех поперечных сечениях внецентренно сжатого (растянутого) бруса действуют следующие внутренние силовые факторы: продольная сила и два

При назначении знака внутреннего усилия здесь использованы общепринятые правила: продольное усилие отрицательно, если оно сжимающее, а изгибающий момент отрицателен, если в точках с положительными координатами Х и Y (первая четверть) под его действием возникают сжимающие напряжения.

Нормальные напряжения в поперечных сечениях бруса определим, используя принцип независимости действия сил. От всех внутренних усилий N, MX и MY – в сечениях возникают нормальные напряжения,

Причём если материал по-разному сопротивляется растяжению и сжатию ([σ]P ≠ [σ]C), то при положительной сумме слагаемых они сравниваются с [σ]P, при отрицательной с [σ]C.

Положение нейтральной линии можно определить с помощью выражения (12.2), подставив в него выражения (12.1) и приравняв напря-

жения σ нулю. С учётом формул для радиусов инерции IX = iX2·F и IY = iY2·F получим

Так как P/F ≠ 0, то сократив на него, получим

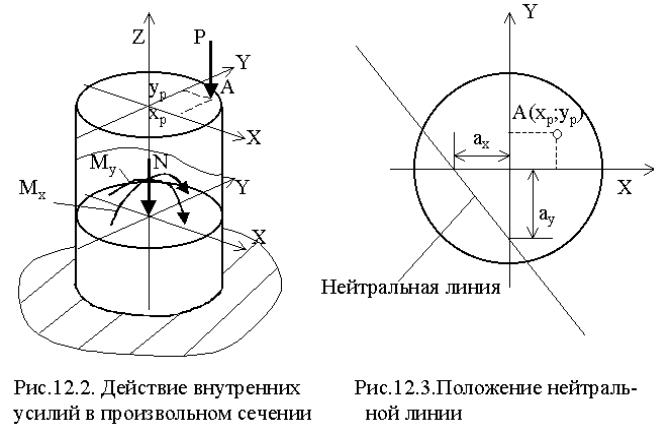
Из формулы (12.5) видно, что нейтральная линия при внецентренном сжатии (растяжении) – это прямая, не проходящая через центр тяжести поперечного сечения (так как при Y = 0, Х ≠ 0 и наоборот). Строить эту прямую удобно с помощью отрезков (аХ; аY), отсекаемых ею на

58

осях координат (рис.12.3)

Очевидно, что точка пересечения нейтральной оси с осью Х имеет координаты аХ; 0 , а с осью Y - аY; 0. Подставляя последовательно эти координаты в выражение (12.5), получим

Знак (-) в формулах (12.6) означает, что нейтральная линия обязательно проходит через четверть, противоположную той, в которой находится точка приложения силы Р (рис.12.3).

12.1. Пример Чугунный короткий стержень, поперечное сечение которого изо-

бражено на рис.12.4, сжимается продольной силой Р, приложенной в точке А.

Требуется: 1) вычислить наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном сечении, выразив эти напряжения через Р, и размеры сечения; 2) найти допускаемую нагрузку Р при заданных размерах сечения и допускаемых напряжениях для чугуна на сжатие [σ]C и на растяжение [σ]Р.

59

Дано: а = 5 см , в = 2 см , [σ]C = 150 МПа , [σ]P = 22 МПа.

Решение 12.1.1. Определим положение центра тяжести фигуры (рис.12.4) в

осях Х1 и Y1.

Разбиваем сечение на две фигуры и определяем положение точек О1 и О2.

12.1.3. Определим квадрат радиусов инерции сечения :