
И.А. Паначев Рабочая программа, контрольные работы и методические указания по их выполнению для студентов заочной формы обучения (сокращенные сроки обучения на базе среднего спец. образования)
.pdf
30
В общем случае напряжённого состояния относительное изменение объёма равно:
εv = |
1−2 µ |
(σ1 +σ 2 +σ 3). |
(8.7) |
|
E
8.3.7. Удельная потенциальная энергия упругой деформации Работа внешних сил при деформации переходит во внутреннюю
потенциальную энергию. Величина потенциальной энергии при упругой деформации зависит от конечной величины приложенных нагрузок.
Удельная потенциальная энергия деформации (в единице объёма) изотропного тела выражается следующим образом через главные на-
пряжения : |
1 |
[σ 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
)]. |
|
|
U = |
+σ 2 |
+σ 2 |
−2µ(σ |
1 |
σ |
2 |
+σ |
2 |
σ |
3 |
+σ |
3 |
σ |
(8.8) |
||||
|
||||||||||||||||||
|
2E |
1 |
2 |
3 |
|
|
|
|
|
|
1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
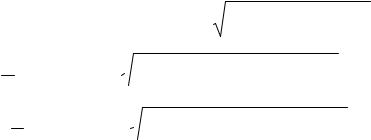
8.4. Пример Стальной кубик находится под действием сил (рис. 8.2), создающих
плоское напряжённое состояние (одно из трёх главных напряжений равно нулю). Требуется найти: 1) главные напряжения и направления главных площадок; 2) максимальные касательные напряжения, равные наибольшей полуразности главных напряжений; 3) относительные деформации εX, εY, εZ; 4) относительное изменение объёма; 5) удельную потенциальную энергию деформаций, если дано σX= 20 МПа,
σY= 40 МПа, τX= 30 МПа.
Рис.8.2.Схема нагружения элемента и положения главных площадок Решение
В соответствии с рис 8.2 имеем:
σX = -20 МПа, σY = 40 МПа, τX =- 30 МПа, τY = 30 МПа.
31 8.4.1. Находим главные напряжения :
σ |
|
= |
1 |
|
|
+σ |
|
+ |
(σ |
|
−σ |
|
2 |
+4τ |
2 |
|
= |
1 |
2 |
σ |
x |
y |
x |
y |
) |
x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
=21 ( −20 +40 +  ( −20 −40 )2 +4( −30 )2 ) = 52,43 МПа,
( −20 −40 )2 +4( −30 )2 ) = 52,43 МПа,
σ3 = 21( −20 +40 −  ( −20 −40 )2 +4( −30 )2 ) = −32,43 МПа,
( −20 −40 )2 +4( −30 )2 ) = −32,43 МПа,
Направления главных площадок : |
|
|
|
|
|
||||
tg2α0 |
= − |
|
2τ y |
= |
−2 |
30 |
=1 |
, |
|
σx −σ y |
−20 |
−40 |
|||||||
|
|
|
|
|
|||||
|
2α0 = arctg1 = 45 o. |
|
|
||||||
|
|
α0 = 22 o30′. |
|
|
|
||||
Этот угол откладываем от вертикали (алгебраически большее из |
|||||||||
главных напряжений) против часовой стрелки и получаем направление σ1, направление σ3 перпендикулярно ему (см. рис. 8.2).
8.4.2. Находим максимальные касательные напряжения, которые будут действовать на площадках, наклонённых под углом 45º к главным
площадкам : |
|
σ1 −σ 3 |
|
|
52,43 −(−32,43) |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
τ max = |
= |
|
= |
42,43 МПа |
||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
8.4.3. Находим относительные деформации по формуле (8.6): |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
εx |
= |
|
1 |
|
( −20 −0,3 40 ) =16 10−5 |
|
|
|
|||||||||||||||||
|
2 105 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
εy = |
1 |
|
|
( −40 −0,3 ( −20 )) = 23 10−5 , |
|
|
||||||||||||||||||||
|
|
2 105 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
εz = |
|
0,3 |
|
( −20 +40 ) = 3 10−5 . |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 105 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
8.4.4. Находим относительное изменение объёма: |
|
|
|
|
|||||||||||||||||||||||||||
|
|
εv = |
1 − 2µ |
(σ1 +σ 2 + |
σ 3)= |
1 − 2 0,3 |
(53,43 + |
0 −32,43)= 4,2 10−5 |
||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
2 105 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
8.4.5. Находим удельную потенциальную энергию деформаций: |
|||||||||||||||||||||||||||||||
|
|
|
U = |
1 |
(σ |
1 |
2 +σ |
2 |
2 |
+σ |
3 |
2 −2µ(σ σ |
2 |
+σ |
2 |
σ |
3 |
+σ |
3 |
σ |
))= |
|||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
2E |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|||||||||
= |
1 |
|
(52,42 + |
(−32,43)2 −2 0,3(32,43 52,43))=12,05 10−3 МПа. |
||||||||||||||||||||||||||||
|
2 2 105 |
|||||||||||||||||||||||||||||||
32
9.КРУЧЕНИЕ КРУГЛЫХ СТЕРЖНЕЙ
9.1.Крутящие моменты
Если нагрузка на прямолинейный стержень (вал) состоит только из моментов Мк, плоскости которых перпендикулярны к оси стержня, то
из шести внутренних усилий в любом сечении остаётся только крутящий момент Мкр.
Внутренний момент Мкр выражается через внешние Мк. Крутящий момент Мкр в сечении равен сумме внешних моментов Мк, расположенных по одну сторону от сечения :
Мкр = ∑Мк(лев) = ∑Мк(пр) . |
(9.1) |
Правило знаков: крутящий момент Мкр считается положительным, когда внешний момент Мк вращает отсечённую часть против часовой стрелки, если смотреть на него со стороны разреза.
9.2. Напряжения и деформации Основные допущения, принятые в теории кручения круглых валов,
выполненных из однородного, идеально упругого материала:
а) гипотеза плоских сечений – сечения плоские до кручения остаются плоскими и при кручении;
б) ось вала при кручении не искривляется; в) удлинение продольных волокон вала отсутствует;
г) радиусы поперечных сечений вала при кручении остаются прямыми, поворачиваясь на определённый угол;
д) в поперечных сечениях вала возникают только касательные напряжения.
Таким образом, кручение можно рассматривать как чистый сдвиг, вызываемый поворотом одного сечения относительно другого. При этом в поперечных сечениях возникают касательные напряжения (см.
рис. 9.1):
τ р = |
Мкр ρ |
, |
(9.2) |
|
Iк |
||||
|
|
ρ – рас- |
||
где τ р – касательное напряжение в рассматриваемой точке; |
||||
стояние от исследуемой точки до оси стержня; Iк – момент инерции
сечения стержня при кручении.
Для круглого сечения Iк = πd4/32.
33
Для кольца Iк = πd4(1 – α)/32, где α = d/D.
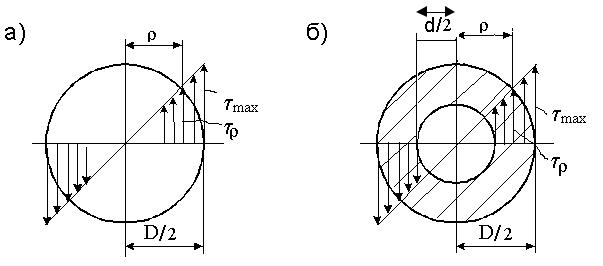
Наибольшие касательные напряжения – у поверхности вала (см.
рис. 9.1, а, б):
τтах = |
Мкр |
, |
(9.3) |
W |
|||
|
к |
|
|
где Wк – момент сопротивления при кручении.
Рис.9.1. Касательные напряжения в поперечном сечении стержня: а) для круглого сечения; б) для кольцевого сечения
Для круглого сечения Wк = πd3/16 , при этом для кольцевого сечения Wк = πD3(1 – α4)/16. Для вычисления Iк и Wк можно пользоваться приближёнными формулами, делающими ошибку в 2%: Iк= 0,1d4;
Wк= 0,2d3 – для сплошного вала, Iк= 0,1D4(1 - α4); Wк=0,2D3(1–α4) – для
полого вала.
Углы закручивания при постоянном крутящем моменте на длине l определяют по формулам:
для сплошного вала
ϕ = |
Мкр 1 |
|
|||
|
|
, |
|
(9.4) |
|
|
|
||||
для полого вала |
|
GIк |
|
||
|
Мкр 1 |
|
|||
ϕ = |
|
||||
|
. |
(9.5) |
|||
GIк( 1 −α4 ) |
|||||
34
9.3.Пример
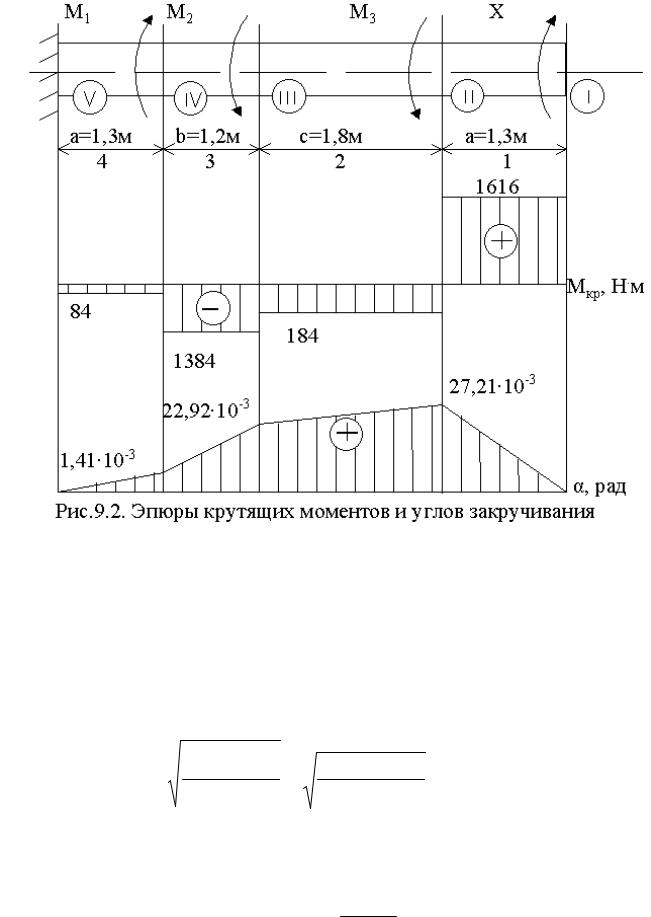
Кстальному валу приложены три известных момента: М1, М2, М3 (рис.9.2). Требуется: 1) установить, при каком значении момента Х угол поворота правого концевого сечения вала равен нулю; 2) для найденного значения Х построить эпюру крутящих моментов; 3) при заданном значении [τ] определить диаметр вала из расчёта на прочность и округлить его до ближайшего большего стандартного значения; 4) построить эпюру углов закручивания; 5) найти наибольший относительный угол
закручивания (на 1 м), если дано: |
а = 1,3 м, |
b = 1,2 м, с = 1,8 м, |
||||||||
М1 = 1300 Н·м, М2 = 1200 Н·м, |
М3 = 1800 Н·м, |
[ τ ] = 55 МПа. |
||||||||
|
|
|
|
|
Решение |
|
|
|
||
9.3.1. Составляем уравнение деформаций, выражающее мысль, что |
||||||||||
угол поворота правого концевого сечения равен нулю. |
||||||||||
|
X (2a + b + c) |
− |
M3 |
(a + b + c) |
− |
M 2 (a + b) |
+ |
M1 a |
= 0. |
|
|
|
|
|
GIk |
|
|||||
|
GIk |
GIk |
|
|
|
GIk |
||||
Подставив цифровые значения, получим |
|
|
|
|||||||
X (2 1,3 +1,2 +1,8)− M3 |
(1,3 +1,2 +1,8)− M 2 (1,3 +1,2)+1,3M1 = 0 |
|||||||||
5,6X − 4,3M3 − 2,5M 2 +1,3M1 = 0,
отсюда Х = 1616 Н·м.
9.3.2. Для найденного значения Х строим эпюру Мкр. На основа-
нии метода сечений имеем, что крутящий момент в сечении численно равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения (формула (9.1)).
Мкр = ∑Мi(пр) = ∑Мi( лев)
Мкр1 = Х= 1616 = 1616 Н·м.
Мкр2 = Х – М3 = 1616 – 1800 = –184 Н·м.
Мкр3 = Х – М3 – М2 = 1616 – 1800 – 1200 = –1384 Н·м.
Мкр4 = Х – М3 – М2 + М1 = 1616 – 1800 – 1200 + 1300 = –84 Н·м.
35
9.3.3. По полученным значениям строим эпюру Мкр (см. рис.9.2). Условие прочности:
|
|
|
|
|
|
|
τтах = |
|
Мкр |
|
|
>[τ], |
|
|||
|
|
|
|
|
|
|||||||||||
|
|
|
|
W |
|
|||||||||||
|
|
|
|
|
|
|
|
|
=πd 3 |
к |
|
|||||
где │М |
кр |
│mах = 1616 Нм, W |
к |
/16, |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d = 3 |
16 |
|
M кp |
|
max = 3 |
16 1616 |
= 0,0532 м. |
|||||||
|
|
|
|
|||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
π [τ] |
|
|
|
3,14 55 106 |
|
||||||
Принимаем по ГОСТ 6636-69 d = 56 мм = 0,056 м.
9.3.4. Строим эпюру углов закручивания. Угол закручивания на участке (формула (9.4):
ϕi = M крili ,
GIк

|
|
|
|
|
|
|
|
|
36 |
|
||
GIk |
= |
Gπd 4 |
= 8 104 106 3,14 0,0564 = 0,772 105 Н м2 , |
|||||||||
|
|
32 |
|
|
32 |
|
|
|
|
|||
где G = 8 104 МПа – модуль упругости при сдвиге. |
||||||||||||
|
|
|
ϕ |
= |
|
1616 1,3 |
|
= 27,21 10−3 рад. |
||||
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
0,772 105 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ϕ2 |
= |
−184 1,8 |
|
= −4,29 10−3 рад. |
|||||
|
|
|
0,772 105 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ϕ3 |
= −1384 1,2 |
= −21,51 10−3 |
рад. |
||||||
|
|
|
|
|
|
|
0,772 105 |
|
|
|||
|
|
|
ϕ4 |
|
|
= |
−84 1,3 |
= −1,41 10−3 |
рад. |
|||
|
|
|
|
|
0,772 105 |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
Находим углы закручивания характерных сечений:
αлев = αпр + ϕi ,
αI = 0,
αII =αI +ϕ1−2 = 27,21 10−3 рад,
αIII =αII +ϕ2−3 = 27,21 10−3 − 4,29 10−3 = 22,92 10−3 рад,
αIV =αIII +ϕ3−4 = 22,92 10−3 − 21,51 10−3 =1,41 10−3 рад,
αV =αIV +ϕ4−5 =1,41 10−3 −1,41 10−3 =0 .
По данным значениям строим эпюру α (см. рис. 9.2)
9.3.5. Находим наибольший относительный угол закручивания
θ = ϕ = Мкр , l GIк
следовательно, наибольший угол закручивания будет на участке, где момент будет максимальным.
I участок: Мкр = 1616 Н·м,
θmax =θ1 = 0,7721616105 = 20,93 10−3 м−1.
37
10. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ
Прочность, жёсткость и устойчивость элементов конструкций во многом определяются формой и размерами их поперечных сечений. В расчётной практике используют так называемые геометрические характеристики сечений.
Площадь сечения является одной из геометрических характеристик, используемых, главным образом, в расчётах на растяжение и сжатие. При расчётах на кручение, изгиб, а также на устойчивость используют более сложные геометрические характеристики: статические моменты, моменты инерции, моменты сопротивления.
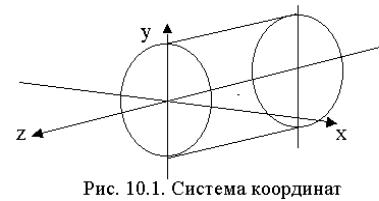
При изложении вопросов геометрических характеристик будем использовать систему координат, показанную на рис. 10.1.
Геометрическими характеристиками данного сечения являются: площадь F, статические моменты SX, SY, радиусы инерции iX, iY, iK,
момент сопротивления WX, WY, WK, моменты инерции |
IX, IY, IK, IXY. |
|
10.1. Площадь плоских сечений (фигур) |
|
|
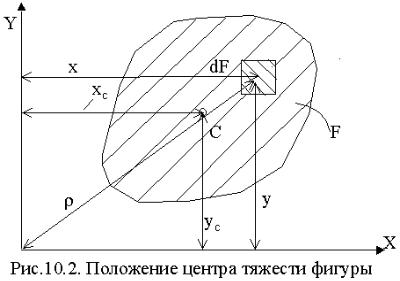
Площадь, ограниченная произвольной кривой, есть (рис. 10.2): |
||
F = ∫dF |
(10.1) |
|
|
F |
|
Для вычисления геометрических характеристик сложных сечений |
||
они разбиваются на конечное число |
n простейших частей. В этом слу- |
|
чае |
n |
(10.2) |
|
||
F = |
∑Fi. |
|
i=1 |
|
|
38
10.2. Статические моменты площади сечения. Центр тяжести сечения
Статическими моментами площади сечения, относительно осей Х и Y, лежащих в плоскости этой фигуры (рис.10.2), называются геометри-
ческие характеристики, определяемые формулами |
|
Sx = ∫ ydF, |
(10.3) |
F |
|
Sy = ∫xdF. |
(10.4) |
F |
|
Если известно положение центра тяжести ХС и YC (рис. 10.2) и его площадь F, то статические моменты определяют по формулам
Sy = FXC , |
(10.5) |
Sx = FYC . |
(10.6) |
Из формул (10.5) и (10.6) следует, что статический момент площади плоской фигуры (сечения) относительно любой центральной оси равен нулю. Обратное положение также справедливо: если статический момент сечения относительно какой-либо оси равен нулю, то эта ось является центральной, т.е. проходит через центр тяжести сечения С.
В зависимости от положения сечения относительно осей координат статический момент может быть положительным или равным нулю.
Из (10.5) и (10.6) могут быть определены координаты центра тяжести фигуры:
XC = |
Sy |
, |
(10.7) |
|
F |
||||
|
|
|
39 |
Sx |
|
|
||
Y |
= |
. |
(10.8) |
||
|
|||||
c |
|
F |
|
||
|
|
|
|||
Для вычисления статических моментов сложной фигуры её разбивают на простые части, для каждой из которых известна площадь Fi и положение центра тяжести (хi, yi). Статические моменты всей фигуры
относительно осей X и Y определяют по формулам
Sx = F1Y1 |
+ F2Y2 +.... + FnYn = ∑(FiYi ), |
|
|
|
i=1 |
Sy = F1X1 |
+ F2 X2 |
+.... + Fn Xn = ∑(Fi Xi ). |
|
|
i=1 |
Координаты центра тяжести сложной фигуры определяют:
|
|
|
Sy |
|
|
∑(F X |
) |
|
||
Xc = |
|
|
|
= |
i i |
|
, |
|||
|
F |
|
∑Fi |
|
||||||
|
|
|
|
|
|
|
|
|||
Y |
= Sx |
= |
∑(FiYi ) |
. |
|
|
||||
|
|
|
||||||||
c |
F |
|
|
|
∑Fi |
|
|
|||
|
|
|
|
|
|
|
||||
(10.9)
(10.10)
(10.11)
(10.12)
10.3. Моменты инерции сечений Осевые моменты инерции площади поперечного сечения бруса от-
носительно осей Х и Y (рис. 10.2):
Ix = ∫Y 2 dF, |
(10.13) |
F |
|
I y = ∫ X 2 dF. |
(10.14) |
F |
|
Полярный момент инерции относительно начала координат (полюса) (рис. 10.2) равен:
Iρ = ∫ρ 2 dF. |
(10.15) |
F |
|
Если через полюс проведена система взаимно перпендикулярных
осей Х, Y, то ρ2 = х2 + y2 (рис. 10. 2) и, следовательно: |
|
Iρ = Ix + I y. |
(10.16) |
