
Методички / Т.А. Балашова Физика. Методические указания по выполнению контрольной работы №1 для студентов заочной формы обучения по курсу общей физики для всех специальностей
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение высшего профессионального образования
«КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра физики
ФИЗИКА
Методические указания по выполнению контрольной работы № 1 для студентов заочной формы обучения
по курсу общей физики для всех специальностей
Составители |
Т.А. Балашова |
|
Н.Н. Демидова |
|
Т.В. Лавряшина |
Утверждено на заседании кафедры Протокол № 2 от 7.10.02
Рекомендовано к печати методической комиссией направления 550600 Протокол № 6 от 19.11.02
Электронная копия находится в библиотеке главного корпуса ГУ КузГТУ
Кемерово 2003
1
Перед выполнением контрольных работ необходимо ознакомиться с общими методическими указаниями [1, с. 4 – 6]. Не приступайте к решению задач, не проработав теоретический материал на соответствующую тему. Обратите внимание на различие в обозначениях вектор-
ных и скалярных величин, например, для вектора силы – F или F , для модуля силы – F.
Контрольная работа № 1
В контрольную работу № 1 включены задачи по физическим основам механики, молекулярной физики и термодинамики.
Задачи 1 – 10 на законы движения тел при прямолинейном и криволинейном движении.
Найти закон движения – значит определить вид зависимости, например, координаты x при прямолинейном движении от времени t, то есть x = x(t ) (задачи 2 – 4). Возможны и обратные задачи: по заданному
уравнению движения определяются величины, характеризующие движение – скорость v (задача 5), ускорение a (задача 6). При этом необходимо помнить, что в общем случае положение материальнойrточки М в
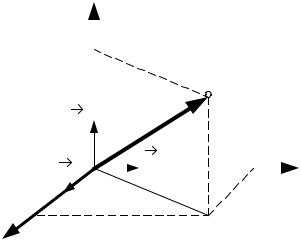
пространстве в момент времени t задается радиус-вектором r или (при использовании декартовой системы координат) тремя координатами x,
y, z (см. рис. 1): rr=xi + yj +zk, где i , j, k – единичные векторы. Изме-
нение положения материальной точки за время |
dt характеризуется |
|||||||||||
вектором перемещения drr |
, а за промежуток времени ∆t |
= t2 |
− t1 – век- |
|||||||||
|
|
|
|
|
|
тором ∆r . Модуль вектора пе- |
||||||
|
Z |
|
|
|
ремещения |
∆r |
совпадает |
с |
||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
пройденным |
путем |
только |
в |
|||
|
|
|
|
|
|
|||||||
|
z |
|
|
|
|
случае прямолинейного |
движе- |
|||||
|
|
|
|
M |
|
ния без изменения направления |
||||||
|
k |
|
|
|
|
вектора |
скорости |
v . |
Вектор |
|||
|
|
|
|
|
скорости |
v |
определяется про- |
|||||
|
|
|
|
j |
y |
|||||||
|
i O |
|
|
Y изводной радиус-вектора |
r |
по |
||||||
|
|
|
|
|
||||||||
X |
x |
|
|
|
времени t: |
vr = drr , |
|
|
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Рис. 1 |
|
|
|
|
dt |
|
|
|
|
2
причем вектор v направлен по касательной к траектории движения в
данной точке. Проекция вектора скорости v на ось ОХ определяется производной координаты х по времени t:
|
vx |
= dx . |
|
|
Вектор ускорения ar |
|
dt |
|
|
при движении материальной точки опреде- |
||||
ляется производной вектора скорости v по времени t: |
||||
|
|
ar = |
dv |
, |
|
|
dt |
||
|
|
|
|
|
а его проекция на ось ОХ – это производная проекции скорости vx по времени t или вторая производная координаты х по времени t (задача 1):
ax = dvx = d 22x . dt dt
Решая задачу 5 по определению скорости v, учтите, если a = ddtv ,
то dv = adt . Следовательно, скорость v определится интегрированием выражения
v = ∫adt +const.
При расчете скорости константу интегрирования, которая зависит от начальных условий, возьмите равной на-
|
|
|
чальной скорости v0 . |
|
|
|
При криволинейном движении, в ча- |
|
τ |
|
стности, при движении по окружности, |
n |
|
|
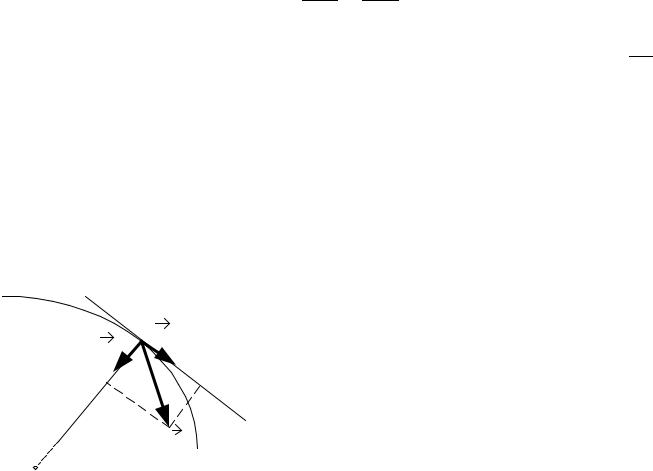
вектор ускорения a удобнее проектировать |
an |
|
aτ |
на направление касательной к траектории и |
|
|
|
нормали к касательной (рис. 2). Тангенци- |
аальное ускорение aτ характеризует быст-
O |
роту изменения скорости по величине: |
|
|
Рис. 2 |
= dv , |
|
a |
|
|
τ |
dt |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
нормальное ускорение an |
– быстроту изменения скорости по направ- |
||||||||||||
лению (τrи nr – единичные векторы выбранных направлений). |
|||||||||||||
В задачах 7 – 9 закон движения задан зависимостью пройденного |
|||||||||||||
пути s от времени t. Для расчета нормального ускорения по формуле |
|||||||||||||
|
|
|
|
|
an |
= |
v2 |
|
|
|
|
||
|
|
|
|
|
R |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
необходимо предварительно определить скорость движения, которая |
|||||||||||||
численно равна первой производной пути s по времени t: |
|
|
|||||||||||
|
|
|
|
v = ds . |
|
|
|
|
|||||
|
|
|
|
|
|
dt |
|
|
|
|
|
||
Для расчета тангенциального ускорения aτ – взять вторую производ- |
|||||||||||||
ную пути s по времени t: |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
a |
= |
dv |
= |
d 2 s |
. |
|
|
|
||
|
|
|
|
|
|
|
|
||||||
|
|
|
τ |
|
dt |
|
|
dt 2 |
|
|
|
|
|
Вектор полного ускорения ar определяется векторной суммой |
|
||||||||||||
|
|
|
ar = aττr + an nr, |
|
|
|
|||||||
а его модуль |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = |
aτ2 |
+ an2 . |
|
|
|
|||||
Закон движения при вращении по окружности может быть задан |
|||||||||||||
зависимостью угла ϕ поворота радиус-вектора r |
от времени t (зада- |
||||||||||||
z |
|
|
ча 6). Поворот радиус-вектора |
rr |
за время |
||||||||
ε |
dωr |
|
dt |
характеризуется вектором |
dϕ |
, направ- |
|||||||
|
< 0 |
|
|||||||||||
|
dt |
|
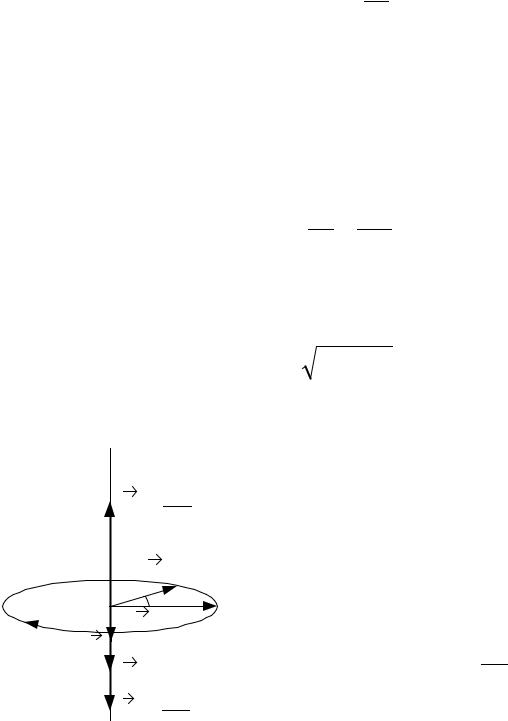
ление которого связано с направлением |
||||||||||
|
|
|
вращения правилом правого винта (прави- |
||||||||||
|
r1 |
dϕ |
лом «буравчика») (рис. 3). Вектор угловой |
||||||||||
|
|
скорости ω определяется производной угла |
|||||||||||
|
r2 |
|
|||||||||||
dϕ |
|
поворота по времени: |
r |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
ωr = dϕ , |
|
|
|||
ω |
|
|
|
|
|
|
|
|
|
|
|||
|
dωr |
|
|
|
|
|
|
|
|
dt |
|
|
|
ε |
поэтому направлен так же, как и вектор dϕ . |
||||||||||||
|
> 0 |
||||||||||||
|
dt |
|
Вектор углового ускорения ε |
при ускорен- |
|||||||||
Рис. 3 |
|
|
ном |
вращении |
совпадает с направлением |
||||||||

4
вектора угловой скорости ωr и направлен противоположно ему при замедленном вращенииr . Угловое ускорение ε равно производной угло-
вой скорости ω по времени:
εr = ddωt .
Причиной, вызывающей быстроту изменения положения тела в пространстве со временем, является сила F при прямолинейномr движении или ее момент M z при вращении твердого тела. Сила F и ускорение ar связаны вторым законом Ньютона: F = mar(задачи 1 – 5). Мо-
мент силы M z и угловое ускорение ε связаны уравнением динамики
вращательного движения:
Mrz = Jzεr = Jz ddtω ,
где Jz — момент инерции твердого тела относительно оси вращения [1,
с. 31, пример 9, с. 42 – 43].
Примечания:
1. В задачах 1 – 9 координата x и пройденный путь s измеряются в метрах (м), время t – в секундах (с), в том числе х0 = 1 м (задача 4).
2. В задачах 7, 10 угол поворота ϕ измеряется в радианах (рад). 3. В условие задачи 4 добавить: v0 = 15 м/с.
4. Угол поворота ϕ и число оборотов N (задача 10) связаны соотношением ϕ = 2πN . С другой стороны, при равноускоренном вращении этот же угол ϕ может быть выражен через начальную угловую скорость ω0 и угловое ускорение ε :
ϕ =ω0 t + εt 2 . 2
Задачи 11 – 20 на тему «Следствия из преобразований Лоренца»: 1. Релятивистское сокращение линейных размеров тела в направлении его движения (задачи 11, 12, 19, 20) происходит согласно форму-
ле
l = l0 1− |
v2 |
, |
|
c2 |
|||
|
|

5
где l0 – собственная длина тела в инерциальной системе, относительно которой тело покоится; l – длина тела, движущегося со скоростью v ;
c– скорость света в вакууме.
Вусловии задач 19, 20 дается относительное изменение линейных размеров, выраженное в процентах. За относительное изменение линейных размеров принимается величина, равная отношению линейного
сокращения ∆l = l0 −l к длине l0 покоящегося тела, то есть
|
ε = |
l0 |
−l |
. |
|
|
|
|
|
|
|||
|
|
|
|
l0 |
|
|
2. Релятивистское замедление времени (задачи 13-15) определяет- |
||||||
ся по формуле |
τ0 |
|
|
|
|
|
τ = |
|
|
, |
|
(1) |
|
1 − v |
2 |
|
|
|||
|
|
|
|
|||
|
c2 |
|
||||
|
|
|
||||
где τ0 – собственное время жизни частицы, отсчитанное по часам,
движущимся вместе с ней со скоростью v ; τ – время, измеренное по неподвижным часам. Согласно формуле (1) движущиеся часы идут медленнее, чем покоящиеся часы.
В задаче 13, зная скорость движения частицы, нужно определить
расстояние, которое пролетит π-мезон до распада l = vτ.
Задача 14 по условию противоположна задаче 13.
3. Теорему о сложении скоростей в релятивистской механике (задачи 16-18), можно представить формулой
u′ = u m v , 1m ucv2
где u и u′ – скорости тела относительно двух инерциальных систем отсчета, движущихся со скоростью v относительно друг друга. При этом знак «–» берется, если скорости u и v совпадают по направлению, а «+» – если скорости направлены навстречу друг другу.
Задачи 21-30 относятся к разделу «Динамика поступательного и вращательного движения».
При решении этих задач используются законы сохранения импульса и механической энергии.
6
1.Закон сохранения импульса (ЗСИ): суммарный импульс замкнутой системы взаимодействующих тел с течением времени не изменяется
n |
r |
(2) |
∑mi vi = const, |
||
i=1
является следствием однородности пространства.
Системы взаимодействующих тел в рассматриваемых задачах (2628) не являются замкнутыми, на них действуют внешние силы. Однако использовать ЗСИ можно, если:
1) векторная сумма всех внешних сил равна нулю
∑n Friвнеш = 0;
i=1
2)сумма проекций всех внешних сил на какую-либо ось равна нулю
|
n |
r |
|
= 0; |
|
∑Fi |
внеш |
||
i=1 |
|
x, y,z |
|
|
3) внутренние силы много больше внешних
Fвнутр >> Fвнеш.
При решении задач на использование ЗСИ необходимо перейти к скалярной форме записи, спроектировав (2) на координатные оси.
2.Закон сохранения механической энергии (ЗСМЭ): полная механическая энергия тела в поле консервативных сил с течением време-
ни не изменяется
E = T + П = const, |
(3) |
где Е – полная механическая энергия, Т – кинетическая энергия, П – потенциальная энергия. Этот закон является следствием однородности времени.
Используйте ЗСМЭ при решении задач 22, 25 и 30.
Для системы взаимодействующих тел, в которых присутствуют неконсервативные силы, например, сила трения (задачи 21, 23, 24, 26, 28), или часть механической энергии переходит во внутреннюю энергию неупруго взаимодействующих тел (задачи 26, 30), полная механическая энергия не сохраняется:
∆E = Aтр |
или |
∆E = Aдеф. |
При этом потенциальная энергия не изменяется, если ее отсчет производится относительно одного и того же уровня.
7
3. Перед решением задач 21 – 23, 25 разберите пример 1.
Пример 1. Шар массой 3 кг катится без проскальзывания по горизонтальной поверхности со скоростью 2 м/с. Определить кинетическую энергию этого шара.
|
|
Решение. |
m = 3 кг |
Катящийся шар участвует в двух движениях, и скорость v |
|
v = 2 м/с |
любой его точки определяется выражением |
|
Т – ? |
|
v = vс +u, |
|
||
где vrс |
– скорость центра масс, то есть скорость поступательного дви- |
|
жения; |
u – линейная скорость, обусловленная вращением вокруг цен- |
|
тра масс, ее модуль
u=ωR.
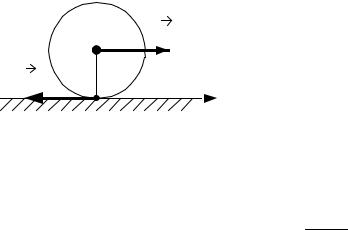
Впроекции на ось Х
|
C |
vc |
v = vс +ωR. |
(4) |
|
|
R |
|
|||
u |
X |
Если скольжения нет, то |
v = 0 , и точка |
||
|
|||||
|
|
|
|||
|
O |
О является мгновенной осью вращения ша- |
|||
|
Рис. 4 |
ра. |
Кинетическая энергия тела, вращаю- |
||
|
|
|
|||
щегося относительно мгновенной оси, проходящей через точку О, |
|||||
|
|
Твр = |
J zω2 . |
(5) |
|
|
|
|
2 |
|
|
Момент инерции J z шара относительно мгновенной оси определяется по теореме Штейнера
J z = J zc + md 2 ,
где J zс = 52 mR2 – момент инерции шара относительно оси, проходящей через его центр масс; d = R – расстояние между осями. Тогда
J z = |
2 |
mR2 |
+ mR2 |
=1,4mR2 . |
|
(6) |
||
5 |
|
|||||||
|
|
|
|
|
|
|
|
|
Решая совместно уравнения (4), (5) и (6), получим |
|
|||||||
|
|
|
1,4mR2 v2 |
|
|
|||
|
|
T = |
|
|
c |
= 0,7mv2 . |
|
|
|
|
|
|
|
|
|||
|
|
вр |
|
2R |
2 |
|
c |
|
|
|
|
|
|
|
|
||
По условию задачи vc = v = 2 м/с, следовательно, кинетическая энергия катящегося шара
T = 0,7 3 кг 22 м/ c = 8,4 Дж.

8
Примечание. Эту задачу можно решить, используя теорему Кёнига: кинетическая энергия механической системы равна сумме кинетической энергии этой системы при ее движении относительно центра масс и кинетической энергии, которую имела бы рассматриваемая система, двигаясь поступательно со скоростью ее центра масс.
Из этой теоремы следует, что кинетическая энергия твердого тела равна сумме его кинетической энергии при поступательном движении со скоростью центра масс и кинетической энергии вращения этого тела вокруг центра масс:
Т = Тпост +Твр = |
mv2 |
+ |
J |
ω2 |
. |
|
c |
z |
|
||||
2 |
2 |
|||||
|
|
|
||||
Момент инерции однородного шара при качении по плоскости J z = const и определяется формулой
J z = 52 mR2 .
Учитывая, что ϖ = vRc , получим
T = |
mv2 |
+ |
2 mR2 |
v2 |
= 0,5mvс2 +0,2mvс2 = 0,7mvс2 . |
|
с |
|
с |
||||
2 |
5 2 |
R2 |
||||
|
|
|
Примечания:
1.Условие задачи 21 трактовать следующим образом.
Сплошной цилиндр массой 0,1 кг катится без проскальзывания с начальной скоростью 4 м/с. Определить кинетическую энергию цилиндра и время до его остановки, если на него действует сила трения 0,1 Н.
2.Перед решением задачи 24 разобрать пример 9 [1, с. 42].
3.При решении задачи 30 необходимо разобрать пример 5 [1, с. 38]. Кроме того, решая эту задачу, учтите, что ЗСМЭ используется в
ней дважды. Шарик, падающий с высоты h1, обладает потенциальной энергией П1 = mgh1 относительно нулевого уровня (плиты).
Эта энергия переходит в кинетическую T1 = |
mv2 |
|
|
1 |
. После взаимо- |
||
2 |
|||
|
|
действия с плитой часть кинетической энергии переходит во внутреннюю энергию (выделяется в виде тепла Q при ударе). Затем
кинетическая энергия T2 = |
mv2 |
|
|
2 |
переходит в потенциальную |
||
2 |
|||
|
|
9
П2 = mgh2 . При описании взаимодействия плиты и шарика используйте второй закон Ньютона в виде
F∆t = ∆(mvr), |
(7) |
где F∆t – импульс силы, переданный плите; ∆(mvr) – изменение импульса шарика.
4.При решении задачи 29 используйте уравнение (7), не забывая при этом, что ∆(mv) = p2 − p1 – это разность двух векторов. Модуль
∆(mv) определяется по теореме косинусов.
5.Решая задачи 21, 25, 28, дополнительно используйте кинематические уравнения
vt −v0 = at; vt2 − v02 = 2as,
где vt и v0 – конечная и начальная скорости, соответственно; a –
ускорение, которое положительно при ускоренном движении (задача 25) и отрицательно при замедленном движении (задача 28); s
– пройденный путь.
Задачи 31 – 40 на тему «Релятивистская механика». При решении задач данной темы необходимо знать следующее:
1. Масса тела зависит от скорости его движения согласно формуле
m = |
m0 |
|
, |
(8) |
|
1 − v |
2 |
||||
|
|
||||
|
c2 |
|
|||
|
|
|
|||
где m0 – масса покоящейся частицы; |
m – масса частицы, движущейся |
||||
со скоростью v .
2. Кинетическая энергия релятивистской частицы (скорость которой сравнима со скоростью света) определяется не по привычной фор-
муле mv2 2 , а как разность между полной энергией mc 2 и энергией
m0 c2 покоя частицы:
T = mc2 − m0 c2 = (m − m0 )c2 .
Или, учитывая зависимость массы от скорости (8), получим, что
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
T = m0c |
2 |
|
|
|
|
|
|
|
|
|
|
−1 . |
|
|
|
1−v |
2 |
|
|
|
|
|
|
|
|
||
|
|
c |
2 |
|||
|
|
|
|
|
|
