Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технический университет им. H.Э.Баумана

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Downloads_1 / 2y_semestr_Lektsia_06

.pdf

Скачиваний:

Добавлен:

24.05.2015

Размер:

169.54 Кб

Скачать

☆

FСОПР

1й курс. 2й семестр. Лекция 6

Лекция 6. «Колебания» (продолжение).

Свободные затухающие колебания. Декремент и логарифмический декремент ко- лебаний. Вынужденные колебания. Установившиеся вынужденные колебания. Механический резонанс.

m		Рассмотрим движение тела в вязкой среде под действием ква-
	Х	зиупругой силы вблизи положения равновесия (например,
	Х	зиупругой силы вблизи положения равновесия (например,
		движение поршня на невесомой пружине). Будем считать, что
		движение поршня на невесомой пружине). Будем считать, что
		сила сопротивления пропорциональна скорости тела:

= -r × v , где r – коэффициент сопротивления (Н×с/м)

Уравнение движения поршня можно записать в виде ma = −kx − rv или

ɺɺx + 2bxɺ+ w20 x = 0

где введены обозначения 2b = r , w02 = k . Это уравнение называется уравнением

m m

свободных затухающих колебаний. Если r = 0, то получаем уравнение свободных

незатухающих колебаний

ɺɺ

= 0

с периодом

x + w0 x

Полная механическая энергия системы равна сумме кинетической и потен-

циальной энергий

mv2

kx2

xɺ2

WМЕХ

= m

+ w02

Для затухающих колебаний механическая энергия не остаётся постоянной а убывает:

dW				ɺ2
	=	d			x
MEX			m
dt					2

		dt

+ w0	2	= m (xx + w0 xx) = mx (x + w0 x) = mx (-2bx) = -rx							2	< 0 .

2	x	ɺɺɺ	2 ɺ	ɺ ɺɺ	2	ɺ	ɺ	ɺ
	2

Будем искать решение уравнения свободных затухающих колебаний в виде x = eλt . Подставив в уравнение и, сокращая, получаем характеристическое уравнение

		λ 2 + 2β ×λ + ω2 = 0 .
			0
Дискриминант этого квадратного уравнения D = 4β					2 - 4ω2		,
					0
значения корней λ =	-2β ±
		4β 2 - 4ω02	= -β ±			.
		4β 2 - 4ω02		β 2 -ω2
				β 2 -ω2
1,2		2	0
		2
Поэтому решение уравнения должно иметь вид

= λ + λ = (− β + β 2 −ω2 )t + (− β − β 2 −ω2 )t = − β ( β 2 −ω2 + − β 2 −ω2 )

x C1e 1t C2e 2t C1e 0 C2e 0 e t C1et 0 C2e t 0 ,

где С1 и С2 – постоянные коэффициенты.

Воспользуемся формулой Эйлера: eiωt = cos (ωt ) + i sin (ωt ) , где i = -1 .

При β 2 -ω02 > 0 решение не описывает колебания.

Колебания будут наблюдаться, если β 2 -ω02 < 0 . Введем обозначение ω2 = ω02 - β 2 .

Тогда 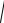β 2 -ω02 = -ω 2 = i ×ω и решение уравнения примет вид

x = A0e− β t sin (ωt +ϕ ) .

1й курс. 2й семестр. Лекция 6

Оно описывает свободные колебания циклической частоты ω, затухающие с тече-

нием времени. Циклическая частота затухающих колебаний ω = ω02 − β2 , период

T = 2π

2π .

ω02 − β2

Необходимым условием колебательного движения является неравенство β < ω0 .

Величина A = A e−βt является амплитудой затухающих колебаний. С течением вре-

мени амплитуда убывает –

говорят, что колебания затухают. Временем затуха-

ния (временем релаксации) называется время τ, за которое амплитуда убывает в е

раз

)

−βt

A t

A0e

= e ,

eβτ = e , откуда τ = 1 .

(

A(t + τ)

A e−β(t +τ)

Число полных колебаний, совершаемое системой за это время Ne = τ =

1 .

βT

Декремент затухания – отношение амплитуд колебаний спустя период

A(t )

A e−βt

= eβT .

A(t + T )

A e−β(t +T )

Логарифмический декремент затухания δ = ln

= βT . Поэтому Ne =

1 .

Величина Q = πNe = π называется добротностью колебательной системы.

2e−2βt

Энергию колебаний в момент времени t можно определить как W =

kA2

2e−2β(t +T )

Убыль энергии за один период W1 −W2

= kA0

2e−2βt

− kA0

= kA0

2e−2βt (1− e−2βT ).

Рассмотрим отношение запасенной энергии к убыли энергии за один период

колебаний

W −W

1− e−2βT .

1й курс. 2й семестр. Лекция 6

При малом логарифмическом декременте затухания δ = βT << 1 воспользуемся разложением

1− e−2βT = 1− (1− 2βT + ...) ≈ 2βT . Т.к,

T =

2π

ω =

и при малых β можно при-

ω2 − β2

ближенно считать ω ≈ ω0 , то

W1 −W2

2βT

2π

2β2π

2π

2β ω

Для затухающих свободных колебаний добротность характеризует ско-

рость убывания энергии при малых затуханиях.

Фазовый портрет свободных затухающих колебаний.

Пусть задан закон колебательного движения

x = A e−βt

sin (ωt + α) .

Тогда скорость при колебаниях

vx = x = −βA0e

−βt

sin (ωt + α) + ωA0e

−βt

cos (ωt

+ α) .

Импульс

sin (ωt + α)

cos (ωt + α) .

= mv

= −mβA e−βt

+ mωA e−βt

px + mβx

Так как

sin (ωt + α)

cos (ωt + α) =

то

A e−βt

mωA e−βt

px + mβx

sin2 (ωt + α) + cos2 (ωt + α) =

= 1 .

A e−βt

mωA e−βt

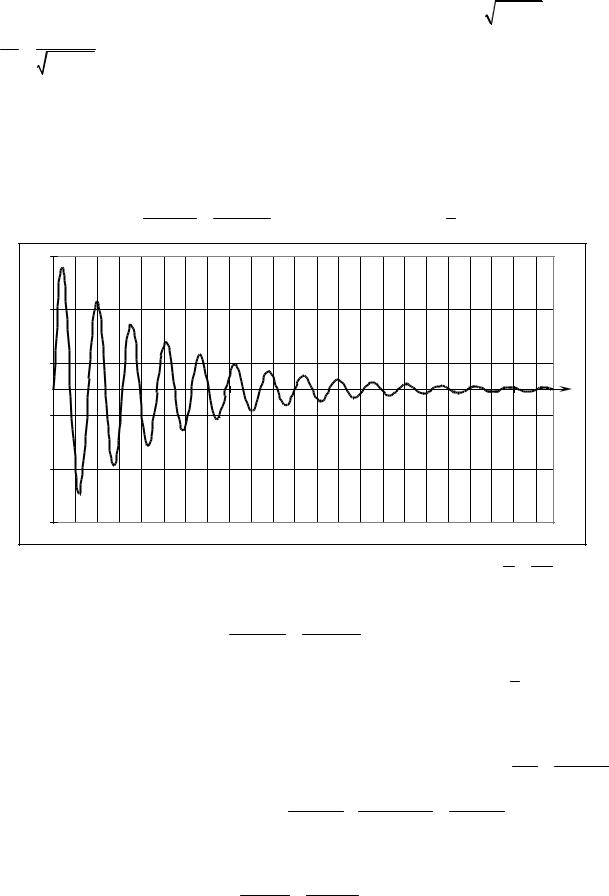
Фазовая траектория представляет собой сужающуюся к нулевой точке спираль (т.к. с течением времени значения x и px стремятся к нулю). Вращение происходит по часовой стрелке.

Вынужденные колебания.

Рассмотрим движение тела в вязкой среде вблизи положения равновесия под действием квазиупругой силы и некоторой периодической силы

F (t ) = F0 cos (Ωt + α) .

Второй закон Ньютона ma = −kx − rv + F (t ) перепишем в виде

x + 2βx				+ ω0 x = f0 cos (Ωt + α)
ɺɺ			ɺ	2
где введены обозначения 2β =	r	,	ω02 =		k	,	f0	=	F0	. Это уравнение называется урав-

	m				m				m

нением вынужденных колебаний. Решением этого обыкновенного дифференциального уравнения является сумма решений однородного и частного решения не-

однородного уравнений.

Однородное уравнение

ɺɺx + 2βxɺ+ ω20 x = 0

является уравнением свободных затухающих колебаний. Частное решение неоднородного уравнения

ɺɺx + 2βxɺ+ ω02 x = f0 cos (Ωt + α)

1й курс. 2й семестр. Лекция 6

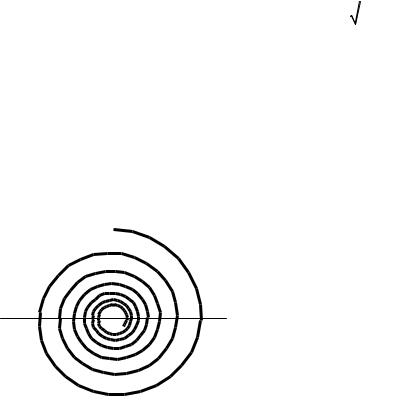
будем искать в виде xB = AB cos (ωBt + αB ) . Изобразим это уравнение на амплитудно-

векторной диаграмме, на которой величине

Ωt+α

ω02 xB = ω02 AB cos (ωBt + αB )

соответствует вектор AB1 , такой

= ω02 AB .

AB2

что AB1

ωBt+αB

Так как

= −ωB AB sin (ωBt + αB ) = ωB AB cos ωBt + αB +

, то

AB3

величине

ωBt + αB

2βxB = 2βωB AB cos

соответствует

на угол π

, длина которого

вектор A

, повернутый относительно вектора A

B 2

AB 2 = 2βωB AB .


ɺɺ		2	2	AB cos (ωBt + αB			+ π) соответствует вектор AB3 ,
Величине xB	= −ωB		AB cos (ωBt + αB ) = ωB	AB cos (ωBt + αB			+ π) соответствует вектор AB3 ,
								= ω	2 A .
повернутый на угол π относительно вектора A						и	A	= ω	2 A .
					B1		B3	B	B

В правой части уравнения величине				f0 cos (Ωt + α) соответствует вектор f0 .
Уравнению	ɺɺ	ɺ	2	будет соответствовать векторная сумма
Уравнению	x	+ 2βx	+ ω0 x = f0 cos (Ωt + α)	будет соответствовать векторная сумма

			AB1 + AB 2		+ AB3 = f0 .

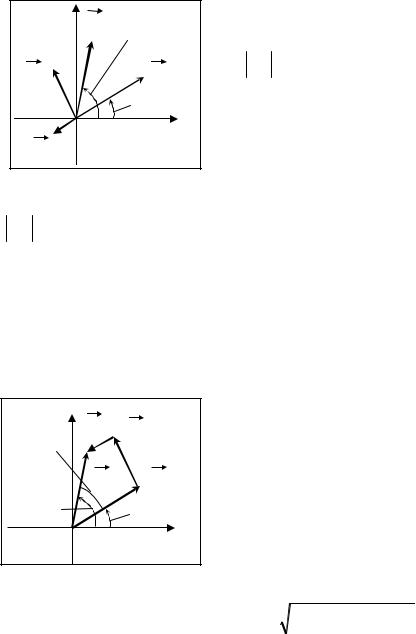
Y	AB3
θ	AB3	AB2
θ
Ωt+α	f0	AB
Ωt+α		ωBt+αB
	0	X

Так как длины векторов не меняются, то это равенство возможно только для случая ωB = Ω . Таким образом,

вынужденные колебания происходят с частотой вы- нуждающей силы.

Из диаграммы следует, что при этом должно выполняться равенство f02 = ( AB1 − AB3 )2 + AB2 2 , поэтому получаем

f02 = (ω20 AB − Ω2 AB )2 + (2βΩAB )2 .

Откуда находим амплитуду вынужденных колебаний:

AB	=			f0		.


			(ω02 − Ω2 )2 + 4β2Ω2
Обозначим θ = α − αB - разность фаз вынуждающей силы и вынужденных колеба-
ний.						2βωB AB			2βΩ
Из диаграммы следует, что tgθ =		AB 2		, т.е. tgθ =		2βωB AB		=	2βΩ
										.
	AB1 − AB3				ω02 AB − ωB		2 AB		ω02 − Ω2	.

Таким образом, при ω0 > Ω получаем, что θ>0 – вынужденные колебания отстают по фазе от вынуждающей силы, а при ω0 < Ω - вынужденные колебания опережают по фазе вынуждающую силу.

Следствие. Под действием периодической силы тело совершает два вида колебаний - свободные затухающие с собственной частотой ω, и вынужденные – с частотой вынуждающей силы Ω. Затухающие колебания с течением времени прекратятся и останутся только вынужденные колебания – их называют установивши-

мися.

1й курс. 2й семестр. Лекция 6

Резонанс – явление резкого возрастания амплитуды установившихся колебаний при приближении частоты вынуждающей силы к собственной резонансной частоте системы.

Найдем, при какой частоте вынуждающей силы амплитуда вынужденных колебаний будет иметь максимальное значение. Для этого найдем экстремум ам-

плитуды:	∂AB	= 0	,
плитуды:	∂Ω	= 0	,	1 f0 (2 (−2Ω)(ω02 − Ω2 ) + 8β2Ω)		f0Ω (ω02 − Ω2 − 2β2 )
		∂A	= −	1 f0 (2 (−2Ω)(ω02 − Ω2 ) + 8β2Ω)		f0Ω (ω02 − Ω2 − 2β2 )	= 0 .
		∂Ω	= −	2 ((ω02 − Ω2 )2 + 4β2Ω2 )3 2	= ((ω02 − Ω2 )2 + 4β2Ω2 )3 2		= 0 .
		B

Первое решение Ω=0 соответствует постоянной сдвигающей силе и отсутствию вынужденных колебаний.

Второе (ограниченное) решение ΩREZ = 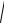ω02 − 2β2 называется резонансной часто-

той системы. Отсюда вытекает условие возникновения резонанса β < ω0 .

Амплитуда колебаний при резонансе

AB _ REZ

(ω02 − ω02 + 2β2 )2 + 4β2

(ω02 − 2β2 )

4β2

ω02

− 4β4

2β ω02

− 2β2

Предельное значение амплитуды вынужденных колебаний при постоянной (сдвигающей) силе (когда Ω=0) – это статическое отклонение на величину

0 B

ω2

Рассмотрим отношение

A0 B

2 2

β2

−

+ 4

ω0

ω0 ω0

При резонансе оно примет вид

AB _ REZ

A0 B

1− 2

β2

ω0

ω02

Обозначим x =

и построим графики зависимости амплитуды от частоты для

различных значений параметров. (График зависимости амплитуды вынужденных колебаний от частоты называется резонансной кривой.).

Зависимость резонансной частоты и резонансной амплитуды от параметра затухания

β/ω0	0,04	0,07	0,1	0,2	0,3	0,4
Ω/ω0	0,99839871	0,995088	0,989949	0,959166	0,905539	0,824621
	8
AB _ REZ	12,5200481	7,178117	5,050763	2,60643	1,840525	1,515848
A0 B	3	7,178117	5,050763	2,60643	1,840525	1,515848
A0 B	3

				1й курс. 2й семестр. Лекция 6							6
				Резонансная кривая
AB
A0 B
12					β	= 0,04
					w	= 0,04
					0
10
8		β	= 0,07
		w
		0					β
6		β					β	= 0,1
6		β	= 0,2				w0
		w					w0
		w
		0					β
4		β					β	= 0,3
4		β	= 0,4				w0	= 0,3
		w
		0
2
											x
0
0	0,2	0,4	0,6	0,8	1	1,2	1,4	1,6		1,8	2
		График зависимости разности фаз от частоты
q
3
2,5	β = 0,4
	w
	0							β
2	β = 0,3							β	= 0,1
2	β = 0,3							w0	= 0,1
	w0							β
1,5	β = 0,2							β	= 0,07
	β = 0,2							w0	= 0,07
1	w0							β
1									= 0,04
									= 0,04
								w
0,5								0
0,5
0											x
0
0	0,2	0,4	0,6	0,8	1	1,2	1,4	1,6		1,8	2

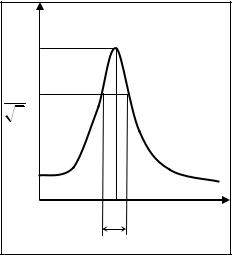
Ширина резонансной кривой ΔΩR - это интервал частоты, в пределах которого ам-

плитуда колебаний отличается от резонансной амплитуды в пределах A(W) ³ AR .

(Т.е. энергии колебаний отличаются не более чем в 2 раза).

1й курс. 2й семестр. Лекция 6

Учитывая, что AB _ REZ =

и AB =

(ω02 − Ω2 )2 + 4β2Ω2

2β ω02 − 2β2

(ω02 − Ω2 )2 + 4β2Ω2

(ω02

− Ω2 )2 + 4β2Ω2

находим

B _ REZ

2β ω2 − 2β2

2β ω2

− 2β2

(ω02 − Ω2 )2 + 4β2Ω2

= 2

ω02 − 2β2

Или

2β

ω02 − 2β2

Откуда получаем квадратное уравнение Ω4 + (

4β2 − 2ω02 ) Ω2 + (ω02 − 4β2 )2

= 0 .

Дискриминант этого уравнения D = 16β2ω02 − 48β4 = 16β2 (ω02 − 3β2 ) .

Корни квадратного уравнения

− (4β2

− 2ω02 )

± 4β

(ω02 − 3β2 )

(Ω2 )

= − (2β2 − ω02 ) ± 2β (ω02 − 3β2 ) .

1,2

Так как (ω02 − 4β2 )2

> 0 , то (Ω2 )

= ω02 − 2β2 ± 2β

> 0 .

(ω02 − 3β2 )

1,2

Откуда находим только положительные решения

Ω1 = ω02 − 2β2 − 2β

и Ω2 = ω02 − 2β2 + 2β

(ω02 − 3β2 )

Поэтому для ширины резонансной кривой получаем

−

ΔΩR = Ω2 − Ω2 = ω02 − 2β2 + 2β

ω02 − 2β2 − 2β

(ω02 − 3β2 )

Следовательно, этот параметр определен при β <

ΩREZ

Найдем отношение

при малом значении β .

ΔΩ

ΩREZ

ω02 − 2β2

ΔΩR

−

2β

+ 2β

− 2β

)

ω0

(ω0

− 3β

) − ω0

(ω0

− 3β

ΩREZ

или

ΔΩR

ΩREZ

+ 2β

(

) −

−

)

ΩREZ

− β

ΩREZ

2β (ΩREZ

− β

ΩREZ ≈ ΩREZ .

ΔΩR 2β

Учтем, что при малых β выполняется ΩREZ							≈ ω0 ≈ ω , поэтому
	ΩREZ		≈	ΩREZ	≈	ω	=	2π	=	π	= Q ,
	ΔΩ	R	≈	2β	≈	2β	=	2βT	=	δ	= Q ,
		R

где величины ω, δ, Q характеризуют затухающие свободные колебания данной колебательной системы.

Рассмотрим также отношение	AB _ REZ	=		1		.
			β
	A0 B	2		1− 2	β2
			ω0		ω02

Для малого затухания β: AB _ REZ ≈ ω0 = Q .

A0 2β

АВ

А0В

1й курс. 2й семестр. Лекция 6

Следствия.

1) Для вынужденных колебаний добротность колебательной системы характеризует резонансные свойства колебательной системы. Добротность равна отношению резонансной частоты к широте резонансной кривой (при малом затухании). Отсюда следует, что чем выше добротность, тем уже

(«острее») резонансная кривая ΔΩR = ΩREZ .

2) Добротность при малом затухании также харак-

Ωтеризует отношение амплитуды при резонансе к

статическому отклонению системы под действием
ΔΩR	AB _ REZ	≈ Q .
постоянной силой такой же величины

	A0

Соседние файлы в папке Downloads_1

#
24.05.2015207.47 Кб232y_semestr_Lektsia_01.pdf
#
24.05.2015190.94 Кб262y_semestr_Lektsia_02.pdf
#
24.05.2015175.71 Кб252y_semestr_Lektsia_03.pdf
#
24.05.2015211.9 Кб242y_semestr_Lektsia_04.pdf
#
24.05.2015206.89 Кб222y_semestr_Lektsia_05.pdf
#
24.05.2015169.54 Кб262y_semestr_Lektsia_06.pdf
#
24.05.2015165.89 Кб282y_semestr_Lektsia_07.pdf
#
24.05.2015208.17 Кб232y_semestr_Lektsia_08_09.pdf
#
24.05.2015101.81 Кб222y_semestr_Lektsia_10.pdf
#
24.05.2015154.09 Кб232y_semestr_Lektsia_11.pdf
#
24.05.2015152.13 Кб232y_semestr_Lektsia_12.pdf