Downloads_1 / 2y_semestr_Lektsia_07

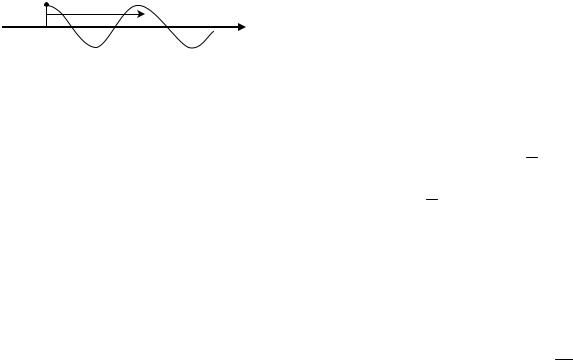
1й курс. 2й семестр. Лекция 7

1

L=x

Рассмотрим поперечную монохромати-

ческую волну, испускаемую некоторым ис-

x=0

точником, находящимся в начале оси X (х=0)

x

X

и совершающим колебания по гармоническо-

му закону.

Пусть его закон колебаний имеет вид ξ = A cos (ω ×t +α ) . Так как ско-

1й курс. 2й семестр. Лекция 7

2

период l =

2π

называется длиной волны. Из соотношения k = ω получаем

2π

=

2π

,

k

l

v

vT

Для функции ξ = A cos (ωt - kx +α )

выполняются соотношения

¶2ξ

= -ω 2 A cos (ωt - kx +α ) ,

¶2ξ

= -k 2 A cos (ωt - kx +α ) ,

1 ¶2ξ

=

1

¶2ξ

откуда

¶t 2

¶x2

ω2 ¶t 2

¶2ξ

= v2 ¶2ξ .

k 2 ¶x2

¶t 2

¶x2

ξ = f1 ( x - vt ) + f2 ( x + vt ) ,

одна из которых -

f1 ( x - vt ) - описывает волновое поле, распространяющееся в по-

ложительном направлении оси X –

его называют убегающей волной, а вторая,

f2 ( x + vt )

- в отрицательном направлениях оси X – её называют набегающей вол-

ной.

Действительно, подставим в волновое уравнение выражение

∂ξ =

∂

ξ = f1 ( x - vt ) + f2 ( x + vt ) .

Тогда

( f ( x - vt ) + f

( x + vt )) = -v × f ¢( x - vt ) + v × f ¢( x + vt ) ,

¶t

¶t

1

2

1

2

¶2ξ = v2 f

¢¢( x - vt ) + v2

f ¢¢( x + vt ) ,

¶t 2

1

2

¶2ξ

∂ξ =

∂

( f ( x - vt ) + f

( x + vt )) = f ¢( x - vt ) + f ¢( x + vt ) ,

= f ¢¢( x - vt ) + f ¢¢( x + vt ) .

¶x

¶x2

¶x

1

2

1

2

1

2

Штрихи означают производные от функций по аргументу.

При подстановке этих соотношений в волновое уравнение ¶2ξ

= v2 ¶2ξ :

¶t 2

¶x2

1й курс. 2й семестр. Лекция 7

3

Скорость движения плоской фазовой поверхности можно найти дифферен-

цированием по времени уравнений

ωt + kx = const

ɺ

или ωt − kx = const : ω + kx = 0 или

ɺ

= 0 . Видно, что скорость вдоль оси v = ±

ω

по величине совпадает со скоро-

ω − kx

k

стью волны, определяемой из волнового уравнения. Таким образом, в волновом

∂2ξ

∂2ξ

уравнении ∂t 2 = v2

∂x2 присутствует квадрат скорости, которая называется фазо-

вой скоростью волны.

Замечание. В общем случае, фазовая скорость может зависеть от парамет-

ров волны (амплитуды, частоты). Для случая, когда скорость зависит от частоты

волны, имеется особое название – дисперсия волн.

Уравнение плоской волны, распространяющейся в произвольном направле-

нии.

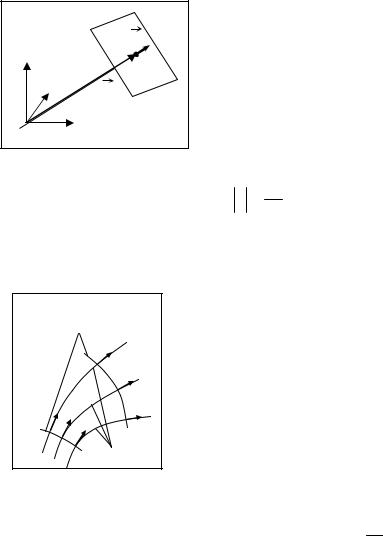
Пусть плоская волна движется в направлении прямой линии, которая про-

ходит через начало координат. Тогда радиус-вектор лю-

k

бой точки, лежащей на этой прямой, тоже лежит на этой

прямой и длина этого вектора равна расстоянию R точки

Z

Y

R

от начала координат. Поэтому уравнение волны, которая

бежит вдоль этой прямой можно записать в виде

X

ξ = A cos (ωt − kR + α ) . Фазовая поверхность волны перпен-

дикулярна этой прямой. Введем волновой вектор k , на-

правленный перпендикулярно фазовой (волновой) поверхности волны в сторону

равна волновому числу. Так как волновой

её движения. Длина вектора k = 2π

λ

вектор параллелен прямой, то можно записать kR = (k ,R) и ξ = Asin (ωt − (k , R) + α ) .

Но для любой плоской волны всегда есть прямая линия, перпендикулярная

Волновая по-

волновой поверхности и проходящая через начало коорди-

нат, поэтому такая форма записи закона движения плоской

верхность

волны является общей.

В чем удобство введения волнового вектора? С его по-

мощью можно определять положения любой волновой по-

верхности. При этом движение волновой поверхности можно

описать с помощью лучей. Луч –

это линия в пространстве,

лучи

касательная к которой в каждой точке направлена как волно-

вой вектор.

Волновое уравнение для движения волны в 3х мерном

пространстве в общем случае имеет вид:

∂2ξ +

∂2ξ

+

∂2ξ

= 1 ∂2ξ .

∂x2

∂y2

∂z2

v2 ∂t 2

Если ввести условное обозначение

∂2ξ

+

∂2ξ

+

∂2ξ = Δξ , то это уравнение можно за-

∂x2

∂y2

∂z2

писать в виде

1й курс. 2й семестр. Лекция 7

4

Dx = 1 ¶2x

,

v2 ¶t 2

где ¶2

+

¶2 +

¶2 = D так называемый оператор Лапласа (Пьер-Симо1нЛапла1с–

¶x2

¶y2

¶z2

французский ученый).

Сферическая волна описывается функцией

x = A0 ×cos (wt + (k ,R) + a)+ A0

×cos (wt - (k ,R )+ b).

R

R

Амплитуда сферической волны обратно пропорциональна расстоянию от центра

волны.

Примеры по выводу волновых уравнений.

Рассмотрим малые поперечные колебания тонкой однородной струны дли-

Y

Y

F

a2

a1

X

F

x

x+Dx

X

ны L и массы m, закрепленной с обоих концов. Пусть сила натяжения струны F

постоянная по величине. Форма струны задается уравнением y(x). Выделим ма-

лый кусок струны, длина которого вдоль оси X равна

x, а масса m. Так как ко-

лебания поперечные, то запишем второй закон Ньютона для куска

m вдоль оси

Y: Dmay = F × sin a2 - F × sin a1

При малых углах (в радианах) справедливо α ≈ sin α ≈ tgα . Но

tga = ¶y

,

tga

2

= ¶y

» ¶y

+ ¶2 y × Dx

(разложение в ряд Тейлора).

1

¶x x

¶x x+Δx

¶x x

¶x2

x

Поэтому Dma

¶y

+

¶2 y

¶y

=

F ×

¶2 y

× Dx .

= F ×

× Dx - F ×

y

¶x x

¶x

2

¶x x

¶x

2

x

x

Т.к. Dm = m Dx и a

y

=

¶2 y

, то m Dx ¶2 y = F ×

¶2 y

× Dx . Окончательно получаем уравне-

L

¶t2

L

¶t 2

¶x2

x

ние

¶2 y = LF × ¶2 y

. Поэтому скорость волны в струне v =

LF .♣

¶t2

m

¶x2

m

Если возвращающая сила пропорциональна

смещению точки от положения равновесия, то вол-

F1

F2

на называется упругой.

Выведем волновое уравне-

ние на примере продольных волн деформации в

X

стержне.

x

x+Dx

Выделим

часть

стержня

длиной

x. Если

площадь

поперечного

сечения

стержня

равна S,

1й курс. 2й семестр. Лекция 7

5

длины части стержня к начальной длине этой части: ε =

x1 −

x

. Если стержень

Dx

и поэтому ε < 0. Та-

сжимается, то его продольные размеры уменьшаются Dx1 < Dx

щений соседних точек Dx1 - Dx = Dξ . Тогда можно записать ε =

x1 − x

=

ξ

. В пре-

Dx

Dx

деле (при

x → 0 ) получаем ε =

∂ξ . С учётом напряжений в сечениях стержня

∂x

F1 = σ x S ,

F2

= σ x+Δx S . Напряжения в сечениях стержня найдем по закону Гука:

σ x

= Eε x , σ x+Δx

= Eε x+Δx , где Е –

модуль упругости материала (модуль Юнга).

Относительная деформация меняется вдоль стержня, поэтому можно счи-

тать, что ε x+Δx

= ε x + ∂ε

x + ... (разложение в ряд Тейлора).

∂x

∂2ξ . Последовательно под-

Ускорение точек выделенной части стержня a

=

x

∂t 2

= F2 − F1 , т.е.

ставим

эти

соотношения

в

уравнения

движения:

max

ρ S x

∂2ξ

= σ x+Δx S − σ x S ,

∂t 2

¶2ξ

¶ε

ρ

∂2ξ

2 − Eε1 , ρDx

+

∂2ξ

= E

∂ε

x

∂t

2 = Eε

¶t

2 = E

ε1

¶x

Dx - Eε1 , ρ x

∂t

2

x .

∂x

С

учетом

равенства

ε = ∂ξ ,

после сокращений,

получаем

дифференциальное

∂x

¶2ξ

=

E

×

¶2ξ

или

∂2ξ

= v2 ∂2ξ .

¶t 2

¶x2

∂t 2

ρ

∂x2

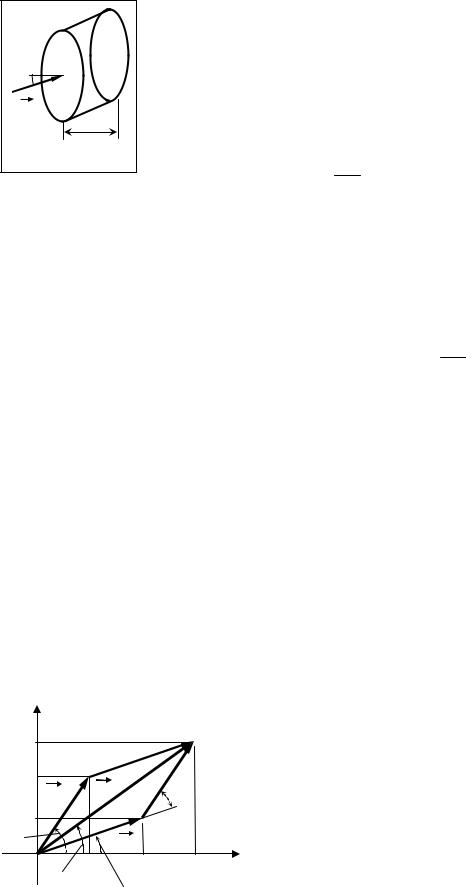
1й курс. 2й семестр. Лекция 7

7

Вектор Умова

Пусть энергия переносится со скоростью v в направле-

нии под углом α к нормали некоторой малой площадки S. То-

S

гда вся энергия, прошедшая через эту площадку за малое вре-

мя dt окажется в области, объем которой dV = S × v ×cos a × dt (на

a

рисунке эта область является косым цилиндром). Если объем-

v

ная плотность энергии равна w, то энергия этого объема

W = w ×dV=w × S × v ×cos a × dt

v×cosa×dt

Мощность переноса энергии через площадку S:

dW = w × S × v ×cos a .

dt

= w × v ,

j

тогда

dW

= j × S ×cos a . Если ввести вектор

× S ,

направленный по нормали к

S

= n

I =

r×w2 A2

S = r×w2

A02

4pR2

= 2pr×w2 A 2

2

2 R2

0

Интерференция волн

Интерференция волн – взаимное усиление

Y

или ослабление волн при их наложении друг на

y∑

друга (суперпозиции волн при одновременном

распространении в пространстве), что приводит

y2

А∑

d

к перераспределению энергии колебаний, устой-

А2

чивому во

времени.

Интерференция волн на-

y1

блюдается

согласно

принципу суперпозиции

j2

А1

X

волн.

O

x2

x1

x∑

Рассмотрим суперпозицию двух волн од-

j∑

ного направления x1 = A1 cos (w1t - k1 x1 + a1 ) и

j1

x2 = A2 cos (w2t - k2 x2 + a2 ) .

1й курс. 2й семестр. Лекция 7

8

xПУЧ n

= ± π × n = ± π × n λ = ±n λ . Соседние пучности находятся друг от друга на рас-

k

2π

2

стоянии λ

- половины длины волны. Точки, где амплитуда стоячей волны равна

2

kx = π ± π × n (n –

целое число). Следовательно, координаты узлов

2

π

π

± π × n

± π × n

1

λ

УЗ

2

2

xn

=

=

λ =

± n

.

k

2π

2

2

1й курс. 2й семестр. Лекция 7

9

1

∂ξ 2

1

∂ξ 2

w = wК + wП

=

ρ

+

E

2

2

∂t

∂x

w =

1

ρ (−ω2 A cos (kx) sin (ωt + θ))2 +

1

E (−k 2 A sin (kx)cos (ωt + θ))2 ,

2

2

w = 2 A2ρω2 (cos2 (kx) sin2 (ωt + θ) + sin2 (kx)cos2 (ωt + θ)) ,

1+ cos (2kx) 1− cos (2[ωt + θ])

1− cos (2kx) 1+ cos (2[ωt + θ])

w = 2 A2ρω2

+

,

2

2

2

2