
Downloads_1 / 2y_semestr_Lektsia_05
.pdf
1й курс. 2й семестр. Лекция 5 |
1 |
Лекция 5. «Колебания»
Гармонические колебания. Векторная диаграмма. Сложение гармонических коле-
баний одного направления равных и близких частот. Сложение взаимно перпен-
дикулярных гармонических колебаний равных и кратных частот. Свободные не-
затухающие колебания. Энергия и импульс гармонического осциллятора. Фазовая траектория. Физический маятник. Квазиупругая сила.
Положение равновесия и квазиупругая сила.
Рассмотрим одномерное движение тела под действием консервативной си-
лы вдоль оси X. Для потенциальной энергии тела вблизи некоторой точки x0 мож-
но записать выражение
W ( x) = W + |
dW |
|
|
×( x - x |
) + |
1 |
|
d 2W |
|
×( x - x |
)2 + ... |
|
dx |
2 dx2 |
|||||||||||
0 |
x |
0 |
|
|
0 |
|
||||||
|
|
|
|
0 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||
Потенциальная энергия и вектор консервативной силы связаны соотношением
F = -gradW
откуда для проекции силы на ось X F = - |
dW |
, т.е. |
||||||||||
|
|
|||||||||||
|
|
|
x |
|
|
|
dx |
|
||||
|
|
|
|
|
|
|
|
|||||
¶W |
|
dW |
|
|
|
|
|
|
||||
|
|
|
|
|
d 2W |
|
||||||
|
|
|
|
|||||||||
|
= - |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Fx = - ¶x |
|
dx |
|
x |
+ dx2 |
|
×( x - x0 ) + ... . |
|||||
|
|
|
|
0 |
|
|
|
|
|
x0 |
|
|
Далее будем предполагать, что точка x0 является положением равновесия, поэто-
W |
|
му должно выполняться условие Fx = - |
dW |
|
= 0 , тогда для |
||||||||
|
dx |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
изменения потенциальной энергии вблизи точки x0 |
|||||||||||
W0 |
|
DW = W ( x) -W » |
1 |
|
d 2W |
|
×( x - x )2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 dx2 |
|
|
|
|
|
|||||||
|
0 |
|
0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F x0 F |
X |
|
|
|
|
|
|
d 2W |
|
×( x - x0 ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
и для проекции силы |
|
Fx » - dx2 |
|
|
|
|||||||
|
|
|
|
|
|
||||||||
U(x0) |
|
|
|
|
|
|
|
|
|
x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рассмотрим случай, когда в точке x0 наблюдается ло- |
||||||||||||
2
кальный минимум потенциальной энергии. Тогда d W > 0 и существует некоторая
dx2

1й курс. 2й семестр. Лекция 5 |
2 |
окрестность точки U(x0), для которой выполняется W ( x) > W0 |
и Fx > 0 при x < x0 , |
Fx < 0 при x > x0 , то есть в этой окрестности вектор силы, действующей на тело,
будет направлен к точке x0. А это значит, что при малых смещения тела из поло-
жения равновесия, сила будет стремиться вернуть тело обратно. Такое положение равновесия называется устойчивым.
Положение равновесия называется неустойчивым, если при малом отклоне-
нии от этого положения возникает сила, стремящаяся увести тело от положения равновесия. Очевидно, в этом случае в точке наблюдается локальный максимум
2
потенциальной энергии d W < 0 .
dx2
2
В случае, когда d W = 0 требуется дополнительное исследование. Итак, выраже-
dx2
ние для консервативной силы вблизи положения устойчивого равновесия можно
|
|
|
|
|
|
|
= −k0 |
x , а величину потенциальной энергии |
||
записать в векторной форме F |
|
|||||||||
|
1 |
|
|
|
d 2W |
|
||||
W = |
|
k0 |
x2 |
+ const, где k0 |
= |
|
|
|
|
. Такая форма записи для консервативной си- |
2 |
|
2 |
|
|||||||
|
|
|
|
dx |
|
|
x= x0 |
|
||
лы вблизи точки равновесия называется квазиупругой силой.
Запишем второй закон Ньютона для тела, движущегося под действием ква-
зиупругой силы вблизи точки устойчивого положения равновесия
max = Fx , где Fx = −k0 ( x − x0 ) .
Введем ось Х так, чтобы x0 = 0 , тогда уравнение движения примет вид max = −k0 x .
С учетом зависимости ax = ɺɺx это уравнение примет вид mxɺɺ= −k0 x или
ɺɺx + ω02 x = 0
где ω02 = k0 > 0 . Это линейное обыкновенное дифференциальное уравнение второго
m
порядка.
Решением этого уравнения являются гармонические функциями от времени t
x = A cos (ω0t + α) или x = A sin (ω0t + β) ,
описывающие смещение от равновесного значения x0 = 0 .

1й курс. 2й семестр. Лекция 5 |
3 |
Замечание. Обе формы записи равноправны. Например, одна переходит в другую
при β = α + π .
2
Так как гармонические функции синус и конус имеют минимальный период
2π, то параметры процесса будут повторяться через минимальный промежуток
времени Т, называемый периодом колебаний: T = ω2π .
0
Учитывая, что величина ν = 1 называется частотой колебаний (единица
T
измерения Гц - Герц), то величину ω = |
2π |
= 2πν называют круговой или цикличе- |
|
||
0 |
T |
|
|
|
ской частотой колебаний (единица измерения с-1.)
Величина А – амплитуда колебаний - это модуль максимального смещения.
По определению A>0 – всегда положительная величина. Аргумент гармонической функции называется фазой колебания, а величина α называется начальной фазой колебаний - это фаза колебаний в момент времени t=0, который обычно на-
зывают начальным моментом времени.
Таким образом, уравнение
ɺɺx + ω02 x = 0
описывает колебательный процесс, параметры которого изменяются пе-
риодически с течением времени. В этом колебательном процессе с течением вре-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɺ2 |
|
|
k0 x |
2 |
|
|
мени сохраняется величина механической энергии W |
= |
mx |
|
+ |
|
= const . Дейст- |
||||||||||||||||||
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
МЕХ |
2 |
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
вительно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dWМЕХ |
|
d |
|
ɺ2 |
|
k0 x |
2 |
|
|
ɺ |
|
x |
|
|
|
|
2 |
|
|
|
|
||
|
|
|
mx |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||
|
|
= |
|
|
|
+ |
|
|
|
= 2m |
|
x |
+ 2k0 |
|
x = mx (x + ω0 |
|
x) = 0 . |
|||||||
|
dt |
|
dt |
2 |
|
2 |
|
|
2 |
ɺɺ |
|
2 |
ɺ |
ɺ |
ɺɺ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Этот колебательный процесс принято называть свободными незатухающими ко-
лебаниями.
1й курс. 2й семестр. Лекция 5 |
4 |
Свободные незатухающие колебания.
Колебания – движения или состояния, параметры которых повторяются во времени. Колебания в той или иной мере встречаются во всех явлениях природы:
от пульсации излучения звезд, движения планет до внутриклеточных процессов или колебаний атомов и молекул, колебаний полей.
В физике особо выделяют механические и электромагнитные колебания (и
их комбинации).
Моделью для изучения механических колебаний является осциллятор – ма-
териальная точка или система, совершающая колебательное периодическое дви-
жение около положения устойчивого равновесия. (Более того, термин осциллятор применим к любой системе, если описывающие ее величины периодически меня-
ются во времени.) Простейшие примеры осцилляторов – грузик на пружине, ма-
ятник.
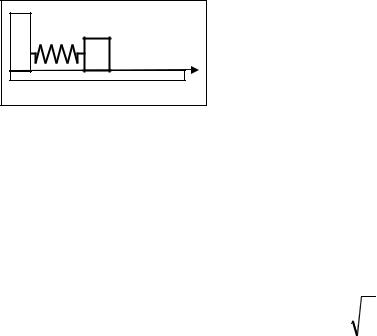
Пример. Груз массы m на невесомой пружине жест- |
кости k движется по гладкой горизонтальной по- |
x |
верхности (пружинный маятник). Найти период его |
колебаний. Сопротивлением воздуха пренебречь. |
Решение. Запишем уравнение его движения в проекции на горизонтальное на- |
правление X |
|
|
|
ma = -F = -k × x или a = - |
k |
x . |
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
УПР |
|
|
|
|
m |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где x – величина растяжения пружины. Т.к. a = x , то получаем уравнение x = − |
|
x . |
|||||||||||||||
|
|
|
|
|
|
|
ɺɺ |
|
|
|
|
ɺɺ |
k |
|
|||
|
|
|
|
|
|
|
|
|
|
m |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь ω 2 |
= |
k |
и период колебаний T = |
= 2π |
m |
. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
m |
|
ω0 |
k |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
ɺ2 |
|
kx |
2 |
|
|
|
||
Механическая энергия груза на пружине W |
= |
mx |
|
+ |
|
.♣ |
|
|
|||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
МЕХ |
2 |
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Пример. Найдем период колебаний математического маятника - матери-
альной точки массы m, подвешенной на невесомой нерастяжимой нити длины l.

1й курс. 2й семестр. Лекция 5 |
5 |
Решение. Рассмотрим движение маятника в тот момент, когда он поднимается.
Отклонение нити от вертикали зададим угловой координатой ϕ. При этом если угол ϕ увеличивается (против часовой стрелки), то касательное ускорение точки направлено против направления движения. Поэтому уравнение движения имеет вид:
d
Z 
ϕ
m
ϕ
mg
maτ = -mg ×sinj.
Вблизи положения равновесия проекция сила тяжести должна быть представлена как квазиупругая сила. Если выполняется ус-
ловие малости колебаний, то sin ϕ ≈ ϕ , поэтому длина дуги ок-
ружности x = lϕ , следовательно, проекция силы тяжести
mg × sinj » mg ×lj = mg × x . Поэтому коэффициент в выражении для
l l
квазиупругой силы k0 = mg . Касательное ускорение связано с уг-
l
ловым ускорением соотношением aτ = e ×l (где ε = ϕɺɺ), поэтому,
|
|
|
|
|
|
|
|
|
|
|
|
ɺɺ |
|
g |
|
×j = 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
после сокращения массы m получим: j + |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
С учетом выражения для циклической частоты w = |
|
|
g |
|
период колебаний имеет |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
вид T = 2p |
l |
|
. Механическая энергия математического маятника |
|||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
ɺ2 |
|
|
k0 x |
2 |
|
|
|
|
|
ɺ |
2 |
|
|
mg |
|
|
x |
2 |
|
|
|
||||||||
|
|
|
|
W = |
mx |
+ |
|
|
|
= |
mx |
|
+ |
|
|
|
. |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
МЕХ |
|
|
2 |
2 |
|
|
|
|
|
2 |
|
|
|
|
l 2 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
При движении по окружности x = lϕ , |
|
x = lϕ , поэтому |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ɺ |
|
ɺ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
2 |
|
ɺ |
2 |
|
|
mg |
|
l |
2 |
j |
2 |
|
|
|
2 |
ɺ2 |
|
|
|
mglj |
2 |
|
|||||||||||
|
|
|
|
W = |
ml |
j |
|
+ |
|
|
|
|
= |
ml |
j |
+ |
|
. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
МЕХ |
2 |
|
|
|
|
l |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Уравнение колебаний для математического маятника можно вывести,
используя уравнение динамики вращательного движения.
Проведем ось Z через точку подвеса перпендикулярно плоскости колебаний маятника, тогда момент инерции материальной точки относительно оси Z:
I z = ml 2 , момент импульса точки L = Iz jɺ направлен вдоль оси Z, а момент силы тя-

|
|
|
1й курс. 2й семестр. Лекция 5 |
6 |
||
жести M z |
= −mgl sin ϕ ≈ −mglϕ (плечо силы тяжести относительно оси d = l sin ϕ ≈ lϕ ) |
|||||
направлен против оси Z. |
|
|
|
|
||
Закон вращательного движения точки вокруг оси Z: |
dLz |
= M z |
или |
|||
|
||||||
|
|
|
|
dt |
|
|
|
|
2 |
ɺɺ |
|
||
|
|
ml |
ϕ = −mglϕ .♣ |
|
||
|
|
Пример. Найдем период колебаний физического маятни- |
||||
|
|
|||||
z |
|
ка - тела массы m, которое может совершать колебания |
||||
|
|
|
|
|
|
|
|
|
под действием силы тяжести (инерции) вокруг горизон- |
||||
ϕ |
|
тальной оси, не проходящей через центр масс тела. Сопро- |
||||
С |
тивлением воздуха пренебрегаем. |
|
||||
|
|
|
||||
|
mg |
Решение. Проведем из центра масс тела C перпендикуляр |
||||
|
|
|
|
|
|
|
|
|
к оси вращения z. Пусть длина этого перпендикуляра рав- |
||||
|
|
на l. |
|
|||
|
|
|
|
|
|
|
Положение тела зададим углом отклонения от вертикали этого перпендикуляра ϕ.
При этом если угол ϕ увеличивается (тело поворачивается против часовой стрел-
ки), то вектор момента импульса L направлен вдоль горизонтальной оси z на нас.
Момент внешней силы тяжести относительно оси z направлен от нас. Рассмотрим проекции на ось z: Lz = Iz ω = Iz ϕɺ , M z (mg ) = −mgl sin ϕ .
Уравнение вращения вокруг оси z: dLz = M z ВНЕШ
dt
Если выполняется условие малости колебаний:
примет вид
или I z ϕɺɺ = −mgl sin ϕ
sin ϕ ≈ ϕ , то уравнение колебаний
ɺɺ |
mgl |
ϕ . |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||||
ϕ = − |
I z |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
С учетом выражения для циклической частоты ω = |
|
mgl |
|
получаем выражение для |
||||||
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Iz |
||
|
|
|
|
|
|
|||||
периода колебаний физического маятника T = 2π |
|
Iz |
. |
|||||||
|
|
|||||||||
|
|
|
|
mgl |
||||||
Приведенной длиной физического маятника называется длина математиче-
ского маятника с таким же периодом

1й курс. 2й семестр. Лекция 5 |
7 |
T = T , 2p |
I z |
= 2p |
lПР |
, l |
|
= |
Iz |
.♣ |
|
|
ПР |
|
|||||
МАТ ФИЗ |
mgl |
|
g |
|
ml |
|
||
|
|
|
|
|
||||
Замечание. Как показано в последних двух примерах, уравнения колебаний мож-
но получить, вводя обобщенную координату - угол и обобщенную квазиупругую
силу – момент силы тяжести.
Математические сведения
Среднее значение (по времени) некоторой величины u(t) за интервал времени (t1,
t2) – |
это такое постоянное значение <u>, для которого выполняется равенство |
||||||||||||||||||||||||||||||||||||||||||||||
t2 |
u (t ) dt = |
t2 |
|
|
|
|
|
|
×(t2 - t1 ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
t2 |
u (t ) dt . |
|
|
|
|
|
|
||||||||||||||
∫ |
∫ |
u |
dt = |
u |
|
поэтому u |
= |
|
(t |
|
|
) ∫ |
Если рассматривать вре- |
||||||||||||||||||||||||||||||||||
|
|
|
|
- t |
|||||||||||||||||||||||||||||||||||||||||||
t |
t |
|
|
|
|
2 |
|
1 |
|
t |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|||
менной интервал (0; + ¥) , то в этом случае |
|
|
u |
= lim |
1 |
∫u |
(t ) dt . |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t→∞ t |
0 |
|
|
|
|
|
|
|
||||
Примеры |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t |
|
|
|
|
1 |
|
|||||
1. Пусть А – |
некоторая константа. Тогда |
|
A |
|
= lim |
|
∫ Adt |
= lim |
|
|
|
At = A . |
|||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t →∞ t |
0 |
|
|
|
t →∞ |
t |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 t |
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2. |
|
|
sin (wt + a) = lim |
|
|
∫ sin (wt + a) dt |
= - |
|
lim |
|
|
|
cos (wt + a) |
0 |
|
= 0 |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t→∞ |
t 0 |
|
|
|
|
|
|
w t →∞ |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
(так −1 ≤ cos ϕ ≤ −1 для любых ϕ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
t |
1+ cos (2wt + 2a) |
|
|
|
|
|
||||||||||||||||
cos2 (wt + a) |
= lim |
|
1 |
|
∫ cos2 (wt + a) dt |
= lim |
|
1 |
|
∫ |
dt = |
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
t →∞ |
t |
0 |
|
|
|
|
|
|
t→∞ |
t |
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
t |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
= |
|
|
|
lim |
|
|
t + |
|
|
sin (2wt + 2a) |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
t |
2w |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 t →∞ |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично cos (wt + a)
cos (wt + a) = 0 ,
= 0 ,  sin2 (wt + a)
sin2 (wt + a) = 1 .
= 1 .
2
Энергия и импульс гармонического осциллятора
Пусть задан закон движения осциллятора x = A cos (wt + a) . Так как колебания неза-
тухающие, то они продолжаются бесконечно долго, поэтому средние значения надо искать на бесконечном интервале (0; + ¥) .
1) Среднее значение проекции импульса для колебательного движения
px = mvx = mxɺ = -mwA sin (wt + a) , тогда  px
px  = -mwA
= -mwA  sin (wt + a)
sin (wt + a) = 0 .
= 0 .

1й курс. 2й семестр. Лекция 5
2) Среднее значение кинетической энергии WK = |
mv2x |
|
= |
px2 |
|
= |
m |
|
ω2 A2 |
|||||||||||||
|
|
2m |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|||||
W |
= |
|
mω2 A2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
K |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3) Среднее значение потенциальной энергии W |
|
= |
kx2 |
|
= |
kA2 |
cos2 (ωt |
|||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
П |
|
2 |
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
W |
= |
kA2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
П |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
С учетом соотношения ω2 = |
k |
получаем, что W |
|
= W = |
kA2 |
. |
||||||||||||||||
|
К |
|
||||||||||||||||||||
|
|
|
|
|
|
m |
|
|
|
|
П |
|
|
4 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3) Найдём среднее значение механической энергии осциллятора
8
sin2 (ωt + α)
+ α)
 WМЕХ
WМЕХ  =
=  WК + WП
WК + WП  =
=  WК
WК  +
+  WП
WП  = kA2 .
= kA2 .
2
Как и следовало ожидать, полная механическая энергия осциллятора остается по-
стоянной.
Фазовая плоскость.
Фазовой плоскостью называется двумерное пространство, координатами в котором является координата точки и проекция импульса (соответственно, обоб-
щенная координата и обобщенный импульс).
Для пружинного маятника из закона сохранения энергии
px |
|
ɺ2 |
|
kx |
2 |
2 |
|
kx |
2 |
|
|
W |
= |
mx |
+ |
|
= |
px |
+ |
|
= const |
||
|
|
|
|
|
|
||||||
MEX |
2 |
2 |
|
|
2m |
2 |
|
|
|||
|
|
|
|
|
|||||||
xследует, что фазовая траектория точки, совершающей сво-
бодные незатухающие колебания – это эллипс
|
p |
2 |
|
kx2 |
kA2 |
|
|
p |
x |
|
2 |
|
x 2 |
|||||
|
x |
|
+ |
|
|
= |
|
|
, |
|
|
|
|
|
+ |
|
= 1, |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||||
|
2m 2 |
|
|
|
|
|
mk A |
|
A |
|||||||||
главные полуоси которого a = |
|
A = mωA = mvmax |
= pmax , b = A . |
|||||||||||||||
mk |
||||||||||||||||||
Замечание. В случае если система состоит из N осцилляторов, то фазовое про-
странство имеет размерность 2N.
Векторная диаграмма.
Рассмотрим радиус-вектор точки М, вращающейся вокруг начала координат с постоянной угловой скоростью ω. Угол между радиус-вектором и осью Х меня-

|
|
1й курс. 2й семестр. Лекция 5 |
9 |
|
|
|
ется с течением времени по закону ϕ = ωt + ϕ0 , где ϕ0 – |
его |
|
Y |
М |
|||
начальное значение. Пусть длина радиус-вектора |
|
|||
y |
|
|||
|
|
|||
|
ϕ |
ОМ =А. Координаты точки М: |
|
|
|
|
|
||
O |
x X |
x = A cos (ωt + ϕ0 ) , y = A sin (ωt + ϕ0 ) |
|
|
|
|
описывают колебания осцилляторов вдоль осей X и Y. |
||
|
|
Данная форма представления колебаний называется |
||
амплитудной (векторной) диаграммой.
Рассмотрим сложение двух колебаний одного направления: пусть два ос-
циллятора совершают колебания вдоль оси Х с циклическими частотами ω1 и ω2
x1 = A1 cos (ω1t + α1 ) и x2 = A2 cos (ω2t + α2 ) .
Зададим эти колебания на векторной диаграмме с помощью векторов.
1-е колебание задаётся вектором A1 , который вращается вокруг начала координат с постоянной угловой скоростью ω1, угол вращения меняется по закону
ϕ1 = ω1t + α1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2-е колебание задаётся вектором A2 , соответст- |
||||
Y |
|
|
|
|
|
|||||
|
|
|
|
|
венно, угол ϕ2 |
= ω2t + α2 . |
|
|||
y∑ |
|
|
|
|
|
|
||||
|
|
|
|
|
Тогда результирующему колебанию xΣ = x1 + x2 |
|||||
y2 |
|
|
|
|
|
|||||
|
|
|
δ |
|
|
|
|
|
|
|
|
А2 |
А∑ |
|
|
сопоставим вектор A = A + A с фазой |
|||||
y1 |
|
|
|
|
|
|
|
Σ |
1 |
2 |
|
|
|
|
|
ϕΣ = ωΣt + αΣ |
|
|
|
|
|
ϕ2 |
|
|
А1 |
|
X |
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
ϕ∑ |
x2 |
x1 |
x∑ |
|
По теореме косинусов |
|
||||
|
|
|
||||||||
|
|
|
ϕ1 |
|
|
2 |
2 |
2 |
− 2 A1 A2 |
cos (π − δ) |
|
|
|
|
|
|
AΣ = A1 |
+ A2 |
|||
Учтем, что cos (π − δ) = − cos δ ,
δ = ϕ2 − ϕ1 = (ω2 − ω1 ) t + α2 − α1 , тогда
AΣ2 = A12 + A22 + 2 A1 A2 cos ((ω2 − ω1 ) t + α2 − α1 )
tgϕ |
|
= |
y |
Σ |
= |
y + y |
|
или tg (ω t + α |
|
) = |
A1 sin (ω1t + α1 ) + A2 |
sin (ω2t + α2 ) |
. |
||||
|
|
1 |
|
2 |
|
|
|
|
|
||||||||
|
Σ |
|
xΣ |
x1 |
+ x2 |
|
Σ |
Σ |
|
A1 cos (ω1t + α1 ) + A2 |
cos (ω2t + α2 ) |
|
|||||
|
|
|
|
|
|
|
|
||||||||||
Соответственно, tg (αΣ ) = |
A1 sin (α1 ) + A2 |
sin (α2 ) |
. |
|
|
||||||||||||
A1 cos (α1 ) + A2 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
cos (α2 ) |
|
|
|||||
1й курс. 2й семестр. Лекция 5 |
10 |
Остановимся подробнее на двух частных случаях.
1) Пусть A1 = A2 := A , ω1 = ω2 := ω . Тогда AΣ2 = 2 A2 + 2 A2 cos (α2 − α1 ) = 2 A2 (1+ cos (α2 − α1 )) .
Амплитуда результирующего колебания в этом случае не зависит от времени.
Если разность начальных фаз колебаний α2 − α1 = 2πn , где n – целое число, то на-
блюдается усиление колебаний AΣ = 2 A .
Если разность начальных фаз колебаний α2 − α1 = π + 2πn , где n – целое число, то колебания гасят друг друга AΣ = 0 .
Для вывода формулы результирующего колебания воспользуемся соотно-
шением
|
|
β |
|
− β |
|
|
β |
2 |
+ β |
|
|
cos β1 + cos β2 |
= 2 cos |
|
2 |
1 |
cos |
|
1 |
|
, поэтому, учитывая четность косинуса: |
||
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
α |
|
− α |
|
|
|
α |
2 |
+ α |
|
xΣ = x1 + x2 |
= 2 A cos |
|
2 |
1 |
cos |
ωt + |
|
1 |
|
||
|
|
2 |
|
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
||
Амплитудой должно быть выражение, не зависящее от времени, но амплитуда не может быть отрицательной величиной, следовательно
|
|
|
|
|
|
|
|
AΣ = 2 A |
|
|
|
|
|
|
α |
2 |
− α |
|
|
, |
|
|
|
|||||
|
|
|
|
|
|
|
|
cos |
|
1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
− α |
|
|
|
|
|
|
|
|
α |
2 |
+ α |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
xΣ |
= 2 A |
cos |
|
2 |
1 |
|
|
cos |
|
ωt + |
|
|
|
1 |
+ θ . |
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
α |
2 |
− α |
|
|
|
|
|
|
|
α |
2 |
− α |
|
|
|
|
|
|
|
|
|||||||
Если cos |
|
1 |
> 0 |
, то θ = 0 , если cos |
|
|
|
|
1 |
< 0 то θ = π . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
2) Рассмотрим случай, когда амплитуды одинаковые A1 = A2 := A , но частоты отли- |
||||||||||||||||||||||||||||
чаются на небольшую величину ω1 = ω , |
ω2 = ω + Δω , |
Δω << ω . Для упрощения при- |
||||||||||||||||||||||||||
мем, что α1 = 0 и α2 |
= 0 . Аналогично предыдущему случаю, получаем |
|||||||||||||||||||||||||||
|
|
|
|
|
x |
= x + x |
= 2 A cos |
Δω t cos |
ωt + Δω t |
. |
||||||||||||||||||
|
|
|
|
|
Σ |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
Пренебрегая в выражении для фазы второго сомножителя величиной Δω по срав-
нению с ω, получаем:
