
Berrar D. et al. - Practical Approach to Microarray Data Analysis
.pdf
294 |
Chapter 17 |
where |
is the computed chi-square value (Sheskin, 2000) that measures |
how far the observed frequencies deviate from the expected frequencies, and n is the total number of observations in the contingency table. The range of c is from 0 to 1, where zero indicates no association.
3.6Statistical Tests of Correlation
After assessing the strength of association in the observations, we would like to know whether the association in the observed samples can be generalized to the population. For example, the relationship between blood pressures and angiotensin gene expression levels in the 10 mice we studied may be interesting, but are they representative of the entire mouse population? Sometimes we rephrase this question by asking whether the results from the observations could have occurred by chance alone, or whether some systematic effect produced the results.
Different statistical test procedures are designed for answering this question. Details of the test procedures of Pearson’s product-moment correlation coefficient, Spearman’s rho, Kendall’s tau, and chi-square test can be found in (Sheskin, 2000). They are easily accessible from any statistical package such as S-Plus (Seattle, WA), SAS (Cary, NC), SPSS (Chicago, IL) or R (Ihaka & Gentleman, 1996).
4.MINING ASSOCIATION RULES
In the previous section, we discussed how to statistically measure and test the association between two variables. That approach is only applicable when we know which two variables are of interest. In other words, we must have a hypothesis before hand. That scenario is not always true for microarray and other genomic studies, where we have a huge data set but little prior knowledge of the relationship among the variables. Thus, the methodologies from Knowledge Discovery in Databases (KDD), or data mining, should also be discussed here. Instead of testing a specific hypothesis of association, association rules mining algorithms discover the intrinsic regularities in the data set.
The goal of association rules mining is to extract understandable rules (association patterns) from a given data set. A classic example of association rules discovery is market basket analysis. It determines which items go together in a shopping cart at a supermarket. If we define a transaction as a set of items purchased in a visit to a supermarket, association rules discovery can find out which products tend to sell well together. Marketing analysts can use these association rules to rearrange the store shelves or to design

17. Correlation and Association Analysis |
295 |
attractive package sales, which makes market basket analysis a major success in business applications.
4.1Association Rules
Definition 17.1. Association Rules |
|
|
|
|
Let |
be a set of m items. Let D be |
a data set of n business |
||
“transactions” as defined above |
where each |
“transaction” |
||
consists |
of a set of items such that |
Note, |
that the |
items in each |
transaction are expressed as yes (present) or no (absent); the quantity of items bought is not considered. The rule describing an association between the presence of certain items is called an association rule. The general form
of an association rule is |
indicating “if A, then B”, where |
|
and |
A and B are item sets that can be either single items or a |
|
combination |
of multiple |
items. A is called the rule body (also called an if- |
clause) and B is the rule head (also called a then-clause). The breakdown of transactions according to whether A and B are true are given in Table 17.4.
Definition 17.2. Support |
|
For the association rule |
the support (also called coverage) is the |
percentage of transactions that contain all the items in A and B. It is the joint probability of finding all items in A and B in the same transaction.
Definition 17.3. Confidence |
|
|
For the association rule |
the confidence (also called accuracy) |
is the |
number of transactions where B occurs along with A as a percentage |
of all |
|
transactions where A occurs, with or without B. It is the conditional probability within the same transaction of finding items in B, given the fact that the items were found in A.

296 |
Chapter 17 |
To better understand the association rules and their measure of confidence and support, let us consider a simple supermarket data set.
An association rule can be presented as
{butter, milk} |
{bread} |
(confidence: 75%, support: 50%), |
where the rule body A = {butter, milk} and the rule head B = {bread}. The contingency table for the rule body and the rule head in this example is given shown in Table 17.5.
This rule means that a person who buys both butter and milk is also very likely to buy bread. As we can see from this example, support and confidence further characterize the importance of the rule in the data set.
The support of the rule is the percentage of transactions where the customers buy all three items: butter, milk and bread.
A higher percentage of the support will ensure the rule applies to a significant fraction of the records in the data set. In other words, support indicates the relative frequency with which both the rule body and the rule head occur in the data set.
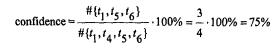
17. Correlation and Association Analysis |
297 |
However, support alone is not enough to measure the usefulness of the rule. It may be the case that a considerable group of customers buy all three items, but there is also a significant amount of people who buy butter and milk but not bread. Thus, we need an additional measure of confidence in the rule.
In our example, the confidence is the percentage of transactions for which bread holds, within the group of records for which butter and milk hold. The confidence indicates to what extent the rule predicts correctly.
Both support and confidence are represented by a number from 0% to 100%. A user-defined threshold (for example, 10% for support, and 70% for confidence) is used as a cutoff point for the mining algorithm to extract the rules from the data set (see the next section).
4.2 Machine Learning Algorithms for Mining Association Rules
Association rules can be discovered by the Apriori algorithm (Agrawal et al., 1996) that involves two main steps. The first step is to find item sets whose support exceeds a given minimum threshold, and these item sets are called frequent item sets. The second step is to generate the rules with the minimum confidence threshold. Mining association rules in large data sets can be both CPU and memory-demanding (Agrawal & Shafer, 1996). For a data set with many items, checking all the potential combinations for the items in step one is computationally expensive, since the search space can be very large (Hipp et al., 2000). There have been many attempts to efficiently search the solution space by either breadth-first or depth-first algorithms. Besides the commonly used Apriori algorithm, there are improvements such as parallel algorithms (Agrawal and Shafer, 1996), Direct Hashing and Pruning (DHP) (Park et al., 1997), Dynamic Itemset Counting (DIC) (Brin et al., 1997), FP-growth (Han et al., 2000), and Eclat (Zaki et al., 1997). For a review of different association rules mining algorithms, see Zaki (2000) and Hipp et al. (2000) For a discussion on generalizing association rules to handle interval data, see Han & Kamber (2001). Finding association rules is a data mining procedure, but not in the framework of statistical testing of associations. Silverstein et al. (1998) discussed how to utilize the chi-square test for independency in association rules mining. Association rules mining have been implemented in many data mining packages such as Clementine (SPSS, Chicago, IL), PolyAnalyst (Megaputer, Bloomington, IN), and Intelligent Miner (IBM, Armonk, NY).

298 |
Chapter 17 |
5.CAUSATION AND ASSOCIATION
It is always tempting to jump to cause-and-effect relationships when observing an association.
In a properly designed experimental study, we should often be able to infer causal relationships. For example, if we manipulate the expression of gene A in animals, and then measure their blood pressure, we might be able to establish that a high level of gene A increases blood pressure. In an observational study, on the other hand, we have no control over the values of the variables in the study. Instead we are only able to observe the two variables as they occur in a natural environment. For example, we randomly pick several mice from the population and measure their expression levels for gene A and blood pressure. In this case, we are not able to infer the causal relationship. It could be that gene A increases blood pressure, or the increased level of gene A is not the cause but the consequence of increased blood pressure.
Generally, observation of association from a stochastic process does not warrant causal relationships among the variables. In such cases, the hypothesis on causation may not be derived from the data itself. Thus, once we find the associated items, we must further analyze them to determine what exactly causes their nonrandom associations.
The explanations of association are illustrated in Figure 17.2.
For further discussion of computational methodologies to discover causal relationships, the reader should refer to Glymour & Cooper (1999), and Chapter 8 of this book.
6.APPLICATIONS IN MICROARRAY STUDIES
A number of supervised and unsupervised machine learning methodologies have been applied to microarray studies. Correlation coefficients have been
17. Correlation and Association Analysis |
299 |
the building blocks for many of these studies, including algorithms from simple clustering to the real challenge of inferring the topology of a genetic regulation networks.
6.1Using Correlation Coefficients for Clustering
Clustering has been a commonly used exploratory tool for microarray data analysis. It allows us to recognize co-expression patterns in the data set. The goal of clustering is to put similar objects in the same group, and at the same time, separate dissimilar objects. Correlation coefficients have been used in many clustering algorithms as a similarity measure. For example, in the Eisen’s Cluster program (Eisen et al., 1998), Pearson’s rho, Spearman’s rho, and Kendall’s tau are available for hierarchical clustering.
6.2Associating Profiles, or Associating Genes with Drug Responses
Hughes et al. (2000) utilized Pearson’s product moment correlation coefficient (r) to conclude that deletion mutant of CUP5 and VMA8, both of which encode components of the vacuolar H+-ATPase complex, shared very similar microarray profiles with an r = 0.88; as a contrast, when the CUP5 mutant is compared with an unrelated mutant of MRT4, the correlation coefficient is r = 0.09.
Correlation studies have been used as a major strategy to mine the NCI60 anticancer drug screening databases (Scherf et al., 2000). Readers can use the online tools at http://discover.nci.nih.gov/arraytools/ to correlate gene expression with anticancer drug activities.
In Figure 17.3, we demonstrate that the anticancer activity of the drug L- asparaginase is negatively correlated with the asparagine synthetase gene. It corresponds with our pharmacological knowledge that L-asparaginase is an enzyme that destroys asparagines that are required by the malignant growth of tumor cells, whereas asparagine synthetase produced more asparagines in the cell.

300 |
Chapter 17 |
6.3Inferring Genetic Networks
The problem of inferring a genetic network can be formulated as following: given a data set of n genes which are the nodes in the network, and an n by m data matrix where each row is a gene (a total of n genes) and each column is a microarray experiment (a total of m experiments), find the network regulatory relationships among the genes using efficient inference procedures; i.e., finding the connecting topology of the nodes. This problem is also called reverse-engineering of the genetic network.
Inferring the genetic network from experimental data is a very difficult task. One simplification is to assume that, if there is an association between the two genes, then it is more likely that the two genes are connected in the genetic network. This way, the edges that connect the nodes (i.e. the regulations between the genes) could be inferred.
Lindlof and Olsson (2002) have used the correlation coefficient to build up the genetic network in yeast. Waddell and Kishino (2000) have explored the possibility of constructing the genetic network using partial correlation coefficients. All of these studies are preliminary, and they have not yet met the expectation of experimental biologists.

17. Correlation and Association Analysis |
301 |
6.4Mining Association Rules from Genomic Data
As opposed to using the network metaphor, the genetic regulatory machinery can also be expressed as a set of rules. For example, we can express the knowledge of genes A, B and C in the following form:
to indicate if gene A and gene B are turned on, then gene C is also turned
on.
Thus, reverse engineering the genetic network can also be formulated as deducing rule sets from data sets, where the association rules mining algorithms are applicable.
To apply association rules mining algorithms to microarray data sets, we can treat each microarray experiment as a transaction and each gene as an item. However, there are problems associated with this approach. First, the expression data have to be discretized since many mining algorithms can only efficiently interpret discretized variables. Secondly, unlike market basket analysis, for microarray data the number of items (genes) is much larger than the number of transactions (microarray experiments). This implies a huge search space when the mining algorithm tries to enumerate the possible combinations in the item sets. For example, even only selecting 4 genes as a set from a data set containing 10,000 genes, results in 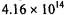 choices. Even with efficient pruning strategies, this algorithm still requires an immense amount of CPU time and memory. Thus, it is a novel computational challenge to apply association mining in microarray data.
choices. Even with efficient pruning strategies, this algorithm still requires an immense amount of CPU time and memory. Thus, it is a novel computational challenge to apply association mining in microarray data.
Berrar et al. (2002) discussed a strategy for discretizing the expression values by a separability score method; as well as a strategy for feature selection to reduce the search space for the Apriori algorithm. An application to the NCI-60 anticancer drug screening data set was demonstrated.
302 |
Chapter 17 |
As illustrated in Table 17.6, after discretizing the numerical data into high (H), medium (M) and low (L) values, a rule can be derived to indicate the intrinsic regularities in this data set:
if Gene_X = H and Gene_Y = H and Gene_Z = H and Drug_A = H and Drug_B = H and Drug_C = H
then Class = CNS.
(coverage: 3/5 (60%); accuracy: 2/3 (67%))
Chen et al. (2001) applied the Apriori mining algorithm to find the association between transcription factors and their target genes. With an ad hoc pruning strategy before and after running the Apriori algorithm, falsepositive results are reduced.
Aussem and Petit (2002) applied function dependency inference, which is closely related to the idea of association rules mining, to a reduced data set of Saccharomyces cerevisiae cell cycle data. They were able to successfully recover some of the known rules.
Berrar et al. (2001) described a case study where the general purpose Apriori algorithm failed due to the complexity of the microarray data. A new algorithm called the maximum association algorithm, tailored to the needs of microarray data, was presented. Its aim is to find all sets of associations that apply to 100% of the cases in a genetic risk group. By using this new algorithm, Berrar et al. found that stathmin is 100% over-expressed in the del (17p) subgroup of B-cell chronic lymphocytic leukemia, a subgroup with a lower survival rate. Stathmin is a signaling molecule that relays and integrates cellular messages of growth and proliferation. It was previously found up-regulated and associated with many high-grade leukemias (Roos et al., 1993). This rule is also of therapeutics interest, since antisense RNA inhibition of stathmin can reverse the malignant phenotype of leukemic cells (Jeha et al., 1996).
Association rules mining is often used as an exploratory method when one does not know what specific patterns to look for in a large data set. The discovered rules always deserve further analysis or experimental tests. With the increased ability to extract rules from large data sets, efficient and userfriendly post-processing of the rules are necessary, since many of the discovered rules are either trivial or irrelevant (Klemettinen et al., 1994).
6.5 Assessing the Reliability and Validity of HighThroughput Microarray Results
Correlation analysis can be used to asses the reliability and validity of microarray measurements. By reliability we mean reproducibility. If two
17. Correlation and Association Analysis |
303 |
microarray measurements conducted from the same sample on two occasions are not correlated, then an error in the measurement system is indicated. Taniguchi et al. (2001) reported that replicated DNA microarray measurements had a Pearson correlation coefficient between 0.984 and 0.995.
In addition to determining the reliability of microarray measurements, correlation analysis can be used to assess the validity of the measurements. By validity, we mean the extent to which our microarray measurements agree with another “standard” methodology. RT-PCR and Northern blots are often considered as the conventional standards for mRNA determination. For example, Zhou et al. (2002) utilized a Pearson correlation coefficient to indicate their microarray results as consistent with Northern blots with an average r = 0.86.
It is important to note that a set of measurements can be reliable without being valid. Microarray measurements could be highly reproducible, with a high test-retest correlation, but the measurements could turn out to be systematically biased. For example, Taniguchi et al. (2001) suggested that the sensitivity of the DNA microarrays was slightly inferior to that of Northern blot analyses.
6.6Conclusions
Correlation coefficients provide a numerical measurement of the association between two variables. They can be used to determine the similarly between two objects when they are merged into a cluster; to assess the association between two gene expression profiles; to establish a connection between two genes in a genetic network; or to asses the agreement between two experimental methodologies.
Mining association rules for microarray data are a novel research challenge. In terms of feasibility, they might require a considerable amount of CPU time and computer memory. In reality, they potentially generate too many trivial or irrelevant rules for biological usefulness. In addition, some established algorithms for market basket analysis do not satisfy the challenge of microarray data (Berrar et al., 2001). However, as an exploratory data analysis tool, the association rules mining technique provides new insights into finding the regularities in large data sets. We expect much more research in this area.
