Колобашкина-Част-1
.pdf
|
. |
|
|
, |
|
|
, |
|
|
, |
- |
|
|
|
|
. |
|
|
, |
|
|
« |
» |
, |
|
|
|
|
, |
|
|
|
|
, |
- |
. |
|
|
|
|
|
2.2. |
|
« |
|
» |
- |
( |
): |
|
|
|
|
|
6 |
3 |
9 |
5 |
|
|
A= 3 |
4 |
5 |
13 . |
|
|
9 |
6 |
4 |
11 |
|
|
|
|
|
, |
- |
, |
0.5 , |
|
. |
|
|



 .
.
1.
W max min aij
max min aij  max [3; 3; 4] = 4.
max [3; 3; 4] = 4.
ij
, |
3. |
|
|
|
2. |
|
|
|
- |
: |
|
|
|
|
|
3 |
3 |
0 |
8 |
R |
6 |
2 |
4 |
0 . |
|
0 |
0 |
5 |
2 |
W min max rij
min max rij  min [8; 6; 5] = 5.
min [8; 6; 5] = 5.
ij
, |
|
3. |
3. |
|
|
W max[ |
min a ij |
(1 ) max aij ] max [6; 8; 7.5] = 8. |
i |
j |
j |
, |
|
A2. |
|
|
|
|
|
81 |

4. |
|
Q1 = Q2 = Q3 = Q4 = 1/4; |
|
|
1 |
n |
|
W max |
|
aij max Mi ; |
|
n |
|||
i |
j 1 |
||
|
i |
||
|
|
|
M1 = 6·l/4 + 3·l/4 + 9·l/4 + 5·l/4 = 23/4;
M2 = 3·l/4 + 4·l/4 + 5·l/4 + 13·l/4 = 25/4;
M3 = 9·l/4 + 6·l/4 + 4·1/4 + 11·l/4 = 30/4.
3, 








 3.
3.
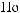












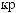












 -
-
















 3,
3, 





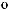




 -
-







 .
.
2.3.























 -
-

















 ,
, 






 -
-
















 .
. 











 ,
, 























 -
-





 .
. 


















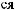

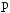 -
-




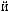








 .
.



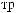
 ,
, 



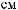




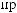











 -
- 















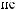







 [1].
[1].
2.3.1. 

 «
«



 »
»
«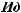


 »
» 









 ,
, 



















 «
«


 »,
», 
















 .
.





 :
:
|| aij || (i = 1, |
, m; j = 1, |
, n); |
Q1, ,Qn |
« |
» |
1, , n; |
|
|
|
. |
|
82 |
|
|

|
. |
|
, |
*= i, |
- |
: |
|
~ |
~ |
max[Q1ai1 ... |
Qn ain ]. |
|
(2.3.1) |
|
a |
maxa i |
|
||||
|
i |
i |
|
|
|
|
|
|
|
|
|
|
. |
|
, |
|
|
|
, |
- |
, |
|
1, |
, |
n |
|
- |
. |
|
1, |
|
|
|
- |
i, |
|
|
|
|
|
1: |
|
|
max ai1 1 . |
|
|
|
|
|
|
i |
|
|
|
|
|
|
« |
» |
j |
|
- |
















 j-
j-



 :
:
|
max aij |
j . |
|
|
i |
|
|
|
, |
|
- |
|
. |
, |
- |
, |
j |
|
- |
|
j . |
|
- |
|
, |
|
- |
Q j |
, |
, |
- |





 :
:
Q1 |
1 |
|
Q2 2 |
... |
Qn |
n . |
|
(2.3.2) |
|
|
|
|
|
|
|
|
- |
. |
|
|
|
|
|
|
|
|
a |
Q1 |
1 |
Q2 |
2 |
... |
Qn n |
. |
(2.3.3) |
|
|
~ |
|
~ |
, |
|
|
|
|
|
> |
|
|
|
|
||
|
|
a |
a . |
|
|
|
|
|
~ |
, |
~ |
|
|
|
(2.3.3), (2.3.1) |
||
a |
a |
|
|
|
||||





 :
:
83

|
|
n |
|
n |
|
|
max |
|
Qj aij |
Qj j C. |
(2.3.4) |
|
i |
j |
1 |
j 1 |
|
|
|
|
|||
|
|
. |
|
|
, |
« |
» |
|
|
, |
|
|
« |
|
» « |
» ( max( f ) = min( f )). |
|
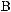








 (2.3.4)
(2.3.4) 












 :
:
n |
|
|
|
(2.3.5) |
min |
Qj ( j |
aij |
) . |
|
i |
1 |
|
|
|
j |
|
|
|
|
|
( |
j |
aij ) |
|
rij , 











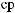









 :
:
|
|
|
n |
|
|
|
|
Q jrij . |
(2.3.6) |
ri |
||||
|
|
j |
1 |
|



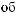


 ,
,












 .
.



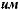

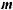








 ,
, 









 -
- 






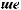

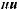









 ri :
ri :
C min |
ri |
. |
(2.3.7) |
i |
|
||












 *,
*, 











 -
-






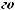


 .
.
|
. |
|
|
|
|
|
|
|
2.3. |
|
|
|
|
|
|
, |
|
|
. 2.4: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
1 |
2 |
3 |
|
4 |
|
|
i |
|
|
||||
|
|
|
|
|
|
|
|
|
= |
|
1 |
|
1 |
4 |
5 |
|
9 |
|
2 |
|
3 |
8 |
4 |
|
3 |
|
|
|
3 |
|
4 |
6 |
6 |
|
2 |
|
|
Qj |
|
0.1 |
0.2 |
0.5 |
|
0.2 |
|
|
|
84 |
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
Qj |
|
|||
« |
» |
j. |
|
|
|
|
|
|
|
|
|
|
||
|
|
, |
|
|
|
« |
|
» |
|
- |
||||
|
, |
|
|
|
( |
|
, |
|
|
|
|
|
|
|
|
) C = 2. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
- |
( |
. 2.5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.5 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
1 |
2 |
3 |
4 |
|
ri |
|
|||
|
|
|
|
|
|
|
||||||||
|
R = |
|
|
1 |
|
3 |
4 |
1 |
0 |
|
1.6* |
|
||
|
|
|
2 |
|
1 |
0 |
2 |
6 |
|
2.3 |
|
|||
|
|
|
3 |
|
0 |
2 |
0 |
7 |
|
1.8 |
|
|||
|
|
|
|
Qj |
|
0.1 |
0.2 |
0.5 |
0.2 |
|
|
|
|
|





















 (2.3.6): r1
(2.3.6): r1  0.1
0.1  3
3  0.2
0.2  4
4  0.5
0.5  1
1  0.2
0.2  0
0  1.6;
1.6;
r2  0.1
0.1 1
1 0.2
0.2  0
0  0.5
0.5  2
2  0.2
0.2  6
6  2.3; r3
2.3; r3  0.1
0.1 0
0  0.2
0.2  2
2  0.5
0.5  0
0  0.2
0.2  7
7  1.8.
1.8.


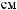



 (2.3.7):
(2.3.7):
|
min |
ri |
min (1.6, |
2.3, 1.8) 1.6 |
2. |
|
|
i |
|
|
|
|
|
|
|
|
|
1.6, |
, |
- |
|
|
|
|
, |
|
- |
, |
|
|
|
|
, . . |
- |
|
1. |
|
|
|
|
|
2.3.2. |
« |
|
» |
|
|
|
« |
» |
|
|
|
|
|
|
« |
» |
j, |
- |
|
|
|
|
|
|
. |
|
|
|
|
|
, |
|
|
- |
|
k |
|
B1, |
, Bk. |
- |
|
|
|
|
85 |
|
|
|

























 ,
, 









 : 1,
: 1, , n .
, n .























 Bl
Bl 

 -
-
j 







 :
:
P(Bl / j )
( j = 1,  , n; l = 1,
, n; l = 1,  , k)
, k) 
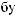





 ,
, 
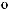








 -
-






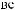

 .
.




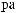

 ,
, 
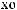

















 -
-





 :
:
|
|
|
|
|| aij |
|| (i = 1, |
, m; j = 1, |
, n); |
|
||
|
« |
» |
|
|
Q1, , |
Qn |
|
|
||
« |
|
» 1, , |
n; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bl |
|
j |
(j = 1, ,n; l = 1, ,k ); |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
, |
|
Bl, |
- |
|
|
|
|
|
|
|
|
|
: |
« |
» |
1, |
, |
n |
|
|
|
|
|
« |
|
» |
|
|
Q1, |
, Qn , |
|
« |
|
» |
- |
||
|
|
Q1l , ..., Qnl , |
|
|
|
|
|
|
|
|
1, |
, |
n |
, |
|
|
|
Bl. |
|
- |
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
Q jl |
|
Qj P(Bl / |
j |
) |
, |
j 1, ..., n. |
(2.3.8) |
|
|
|
|
n |
|
|
|||||
|
|
|
|
Qj P(Bl / |
|
j ) |
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
« |
» Q1, |
, |
Q n 














 Q1l , ..., Qnl ,
Q1l , ..., Qnl , 


 -
-



 *
* 

















 -
-
~* , |
|
|
- |
l |
|
|
|
( |
Bl ). |
|
|
|
. |
|
|
2.4. |
2.3 ( . |
. 2.4) |
- |
|
: Q1 = 0.1; |
Q2 = 0.2; |
Q3 = 0.5; |
|
86 |
|
|

Q4 = 0.2 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
: |
1, |
2, 3. |
- |
|
|
|
|
|
|
|
P(B l / |
j) |
|
|
|
|
|
1, 2, 3, |
4 |
|
|
|
|
|
- |
|||
( |
. 2.6). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
1 |
2 |
3 |
|
4 |
|
|
|
|
Bl |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
B1 |
|
0.2 |
0.9 |
0.4 |
|
0.3 |
|
|
|
|
B2 |
|
0.1 |
0.1 |
0.5 |
|
0.3 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
B3 |
|
0.7 |
0 |
0.1 |
|
0.4 |
|
|
|
|
|
|
|
|
|
, |
|
|
|
, |
|
|
|
|
|
|
|
|
|
. |
|
- |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
. |
|
|
, |
|
|
|
|
|
- |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qj1 , j |
1, ..., 4, |
||
« |
|
» |
1, |
2, |
3, |
4 |
|
|
|
(2.3.8) |
- |
||||||
1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Q11 |
|
|
Q1P(B1 / |
1) |
|
|
|
|
|
|
|||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Q j P(B1 / |
|
j ) |
|
|
|
|
||||
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.1 0.2 |
|
|
|
|
|
0.02 |
0.043; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0.1 |
0.2 |
0.2 |
0.9 |
0.5 |
0.4 |
0.2 |
0.3 |
0.46 |
|||||||||
|
|
||||||||||||||||
|
|
|
|
Q21 |
|
|
Q2 P(B1 / |
2 ) |
|
|
|
|
|
||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||
 Qj P( B1 /
Qj P( B1 /  j )
j )
j 1
|
|
|
0.2 |
0.9 |
|
|
|
|
0.18 |
0.392; |
|
0.1 |
0.2 |
0.2 |
0.9 |
0.5 |
0.4 |
0.2 |
0.3 |
0.46 |
|||
|
|||||||||||
|
|
|
|
|
87 |
|
|
|
|
|
|


Q Q1P(B2 / 1 )
12 4
Qj P(B2 /  j )
j )
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.1 |
0.1 |
|
|
|
|
|
0.01 |
0.029; |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0.1 |
0.1 |
0.2 |
0.1 |
0.5 |
0.5 |
0.2 |
0.3 |
0.34 |
||||||
|
|
|
|||||||||||||
~ |
0.02 |
0.059; |
~ |
|
0.25 |
0.735; |
|
~ |
|
0.06 |
0.177; |
||||
Q22 |
|
|
Q32 |
|
|
Q42 |
|
||||||||
0.34 |
0.34 |
|
0.34 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Q13 |
Q1P(B3 / 1 ) |
|
|
|
|
|
|
|
|||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||
Qj P(B3 /  j )
j )
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.1 |
0.7 |
|
|
|
|
|
|
|
|
0.07 |
0.35; |
|
|
|
|
|
|||||||
|
0.1 |
0.7 |
0.2 |
0 |
0.5 |
0.1 |
0.2 |
0.4 |
|
0.2 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
~ |
|
|
|
|
|
0 |
|
|
0; |
~ |
0.05 |
|
0.25; |
~ |
|
|
0.08 |
0.4. |
|
|
|
|
||||||||||||||
|
Q23 |
|
|
|
|
|
|
|
|
Q33 |
|
|
|
|
|
Q43 |
|
|
|
|
|
|
|
|
|||||||||||||
|
0.2 |
|
|
0.2 |
|
0.2 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. 2.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. 2.8, |
|
- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2, |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2, 3 |
|
- |
||||||||
|
|
|
(2) |
, |
|
|
|
(3) |
(i = 1, 2, 3), |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. 2.8. |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.8 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
(2) |
|
|
|
(3) |
|
|
|
1 |
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
|
|
4 |
|
a |
|
|
a |
a |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
i |
|
|
i |
|
||||||||||||
A1 |
1 |
|
|
|
|
|
|
|
|
4 |
|
|
5 |
|
|
|
|
9 |
4.96 |
|
|
5.533* |
|
5.2* |
|
||||||||||||
A2 |
3 |
|
|
|
|
|
|
|
|
8 |
|
|
4 |
|
|
|
|
3 |
5.395* |
|
|
4.030 |
|
3.25 |
|
||||||||||||
A3 |
4 |
|
|
|
|
|
|
|
|
6 |
|
|
6 |
|
|
|
|
2 |
5.394 |
|
|
5.234 |
|
3.7 |
|
||||||||||||
Qj1 |
0.043 |
|
|
|
|
0.392 |
|
0.435 |
|
|
0.130 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Q j 2 |
0.029 |
|
|
|
|
0.059 |
|
0.735 |
|
|
0.177 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Q j 3 |
0.35 |
|
|
|
|
|
|
|
0 |
|
0.25 |
|
|
|
0.4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
89






 .
.



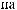

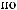




 . 2.8
. 2.8 











 -
-









 .
.
 1,
1, 








 -
-







 2;
2; 













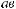
 5.395.
5.395.








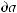




 2
2 

 3,
3, 









 -
-





 1;
1; 












 2
2
5.533, 





 3
3  5.2.
5.2.



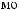











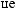









 -
-
|
|
|
. |
|
|
: |
|
|
|
|
3 |
|
|
(l ) , |
a |
P(B ) max |
|
||
a |
||||
|
l |
i |
i |
|
|
l 1 |
|
|
|
|
|
|
|
|
i |
i (i = 1, 2, 3). |
|
|
|
 1,
1,  2
2 
 3.
3.
4
P(B1 ) 
 Q j P(B1 /
Q j P(B1 /  j)
j) 
j 1
 0.1
0.1 0.2
0.2  0.2
0.2  0.9
0.9  0.5
0.5  0.4
0.4  0.2
0.2  0.3
0.3  0.46;
0.46;
4
P(B2 ) 
 Q j P(B2 /
Q j P(B2 /  j)
j) 
j 1
 0.1
0.1 0.1
0.1 0.2
0.2  0.1
0.1 0.5
0.5  0.5
0.5  0.2
0.2  0.3
0.3  0.34;
0.34;
4
P(B3 ) 
 Q j P(B3 /
Q j P(B3 /  j)
j) 
j 1
 0.1
0.1 0.7
0.7  0.2
0.2  0
0  0.5
0.5  0.1
0.1  0.2
0.2  0.4
0.4  0.20.
0.20.
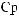

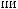





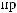


















 -
-
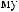

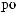


















 :
:
a

 0.46
0.46  5.395
5.395  0.34
0.34  5.533
5.533  0.2
0.2  5.2
5.2  5.403.
5.403.












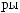
 ,
, 










 -
-














 (2.3.1).
(2.3.1). 















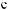



















 :
:
90

 0.043
0.043  1
1 0.392
0.392  4
4  0.435
0.435  5
5  0.130
0.130  9
9  4.956;
4.956; 0.043
0.043  3
3  0.392
0.392  8
8  0.435
0.435  4
4  0.130
0.130  3
3  5.395*;
5.395*; 0.043
0.043  4
4  0.392
0.392  6
6  0.435
0.435  6
6  0.130
0.130  2
2  5.394.
5.394.







 . 2.7.
. 2.7.


 ,
, 















 -
-























 -
-




 .
.










 2
2 3
3