
Колобашкина-Част-1
.pdf

|
|
|
|
0.5 |
1 |
3.5 |
|
2 |
|
|
|
|
|
|
1 |
2 |
3.5 |
. |
|
|
|
|
|
|
|
4.5 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
. |
|
|
|
|
: |
|
|
|
|
|
|
1 |
(1) |
1 |
[1,1]. |
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
SA* = [1 |
0]; |
SB *= [1 |
0 0 0]. |
|
|
|||
|
|
= 0.5. |
|
|
|
|
|
|
|
|
|
|
4.8. |
|
|
|
|
|
|
|
|
1- |
|
|
|
|
|
: |
|
, |
- |
|
1, |
|
|
|
2/3, |
|
2 |
1/3. |
|
|
|
|
x = 1, |
2- |
|
|
|
y |
- |
|
||
|
|
{1, 2}, |
|
|
|
|
1- |
|
||
, |
|
3- |
|
|
|
|
|
z |
|
|
|
{1,2}, |
|
, |
|
|
|
|
|
|
|
|
|
1- |
|
|
|
|
|
2- |
. |
|
|
x = 2, |
2- |
|
|
|
|
y |
- |
|
|
|
|
{1, 2}, |
|
|
|
|
1- |
- |
|
|
, |
3- |
|
|
|
|
|
|
z |
- |
|
{1,2}, |
, |
|
|
. |
|
|
|
, |
|
|
|
|
|
W(x, |
, z), |
|
, |
|
- |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. 4.9. |
|
|
|
|
-2 |
4 |
1 -4 |
3 |
0 -3 |
-5 |
|
|
|
|
|
1 |
2 |
1 |
2 |
1 |
2 1 |
2 |
|
|
|
|
|
|
|
|
A |
|
A |
|
|
|
|
1 |
|
2 |
1 |
B |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
. 4.9 |
|
|
|
|
|
|
|
|
142 |
|
|
|
|

|
|
|
|
|
|
|
- |
|
|
y, z |
|
, |
( {1, 2}) |
|
2- |
|
|
|
|
||||
|
|
|
|
|
|
|
|
, |
1- |
|
|
|
x = 1, z (z {1,2}) |
|
|
3- |
, |
1- |
x = 2. |
, |
- |
||


 1, 2
1, 2


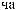
 ,
, 

 2-
2-









 y = 1,
y = 1, 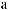
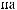 3-
3-


 z = 2.
z = 2.
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
1,1 |
|
, |
2 |
|
|
|
|
1, 2 |
|
|
|
, |
3 |
|
|
|
|
2,1 |
|
, |
4 |
|
|
|
|
2, 2 |
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
1,1 |
|
, |
2 |
|
1, 2 |
|
, |
3 |
|
|
2,1 |
|
, |
4 |
|
|
2, 2 |
|
. |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1, 2 |
|
, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2,1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
: 1) |
x = 1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2) x = 2.







 = 1
= 1 


















 2-
2-

 (
(


 y),
y), 





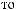

 3-
3- (
(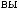


 z).
z).
= 2 |
|
|
: |
- |
2- |
( |
y), |
3- |
( - |


 z).
z).


 = 1,
= 1, 





 2
2 








 2-
2-


 -
-


 y = 1,
y = 1, 





 3
3 








 3-
3-
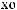


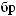

 z = 1.
z = 1. 





W (x,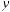 , z) = W (1,1,1) =
, z) = W (1,1,1) = 2.
2.


 = 2,
= 2, 





 3
3 







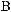
 2-
2-


 -
-


 y = 2,
y = 2, 





 2
2 








 3-
3-





 z = 2.
z = 2. 





W (x,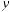 , z) = W (2,2,2) =
, z) = W (2,2,2) = 5.
5.




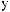













 1-
1-




 -
-







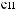







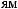
 2/3
2/3  1/3,
1/3, 

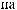






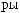


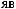














 ,
, 

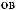



 ,
,

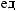

















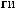



 : (
: ( 2)·2/3 + (
2)·2/3 + ( 5)·1/3 =
5)·1/3 =  3.
3.
143







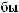










 ,
, 







 -
-



















 .
. .
. 




 ,
,














 1
1 
 2
2 






 -
-









 .
. 

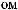










 [x1, x2]
[x1, x2]



 x 1,
x 1, 
















 1-2
1-2  1-
1-





















 {q2, q3},
{q2, q3},













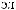



 (
(

























 ),
),  .
. . x1({q2, q3})
. x1({q2, q3}) {1,2}.
{1,2}.



 x2,
x2, 












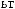



 3
3  1-
1-

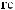 (
(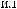

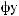





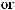













 {q8,
{q8,
q10, q11}), |
|
|
|
|
( |
|
|
|
|
|
), . . |
x2({q8, q10, q11}) {1,2}. |
|
|
|
||
|
, |
4 |
|
: |
|
1 |
[1,1] |
(x1({q2, q3}) = 1, x2({q8, q10, q11}) = 1); |
|||
2 |
[1,2] |
(x1({q2, q3}) = 1, x2({q8, q10, q11}) = 2); |
|||
3 |
[2,1] |
(x1({q2, q3}) = 2, x2({q8, q10, q11}) = 1); |
|||
4 |
[2,2] |
(x1({q2, q3}) = 2, x2({q8, q10, q11}) = 2). |
|||
. 4.10 |
, |
|
|
: |
|
, |
|
|
|
1 |
- |
|
2 |
3 (2-3). |
, |
|
|
|
|
|
(2-3 |
1), |
|
|
|
|
|
|
|
[y1, y2]. |
, |
|
{q4, q7} |
- |
|
|
1 |
2. |
|
|
|
|
, |
|
[y1, y2] |
y1, - |
|
|
|
|
2-3 |
1- |
, |
|
|
|
|
{q4, q7}, |
|
|
|
( |
|
|
|
|
|
), . . y1({q4, |
q7}) |
{1,2}. |
y2, |














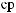


 1
1  1-
1-

 (
(





















 {q5, q6}),
{q5, q6}), 

 -
-











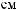


 (
(
























 ),
),  .
. . y2({q5, q6})
. y2({q5, q6}) {1,2,3}.
{1,2,3}.
, |
6 |
: |
1 [1,1] |
(y1({q4, q7}) = 1, y2({q5, q6}) = 1); |
|
|
147 |
|

2 |
[1,2] |
(y1({q4, q7}) = 1, |
y2({q5, q6}) = 2); |
|
3 |
[1,3] |
(y1({q4, q7}) = 1, |
y2({q5, q6}) = 3); |
|
4 |
[2,1] |
(y1({q4, q7}) = 2, |
y2({q5, q6}) = 1); |
|
5 |
[2,2] |
(y1({q4, q7}) = 2, |
y2({q5, q6}) = 2); |
|
6 |
[2,3] |
(y1({q4, q7}) = 2, |
y2({q5, q6}) = 3). |
|
q 1 |
|
1, 2, 3 |
|
|
( |
|
) |
|
0.1, |
0.2, 0.7. |
|
|
|
|
|
|
|
q9, |
1 |
|
|
1/3, |
2 |
|
2/3. |
|
|
|
|
({Ai, Bj}, q, a), |
{Ai, Bj}(i = 1, ,4; j = 1, ,6) |
, |
|
Ai, Bj, |
; |
q 
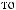







 ;
; 






 .
.



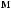 ,
, 






 {Ai, Bj}
{Ai, Bj} 






 q
q 

 -
-
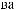
 ,
, 







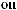
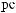










 ,
, 






 ({Ai, Bj}, q, a) = 1;
({Ai, Bj}, q, a) = 1; 















 -
-















 ,
, 
 ({Ai, Bj}, q, a) = 0.
({Ai, Bj}, q, a) = 0.


 ,
, 


 ,
, 









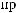







 -
- 

 2
2  [1,2]:
[1,2]:
x1({q2, q3}) = 1, x2({q8, q10, q11}) = 2, 



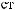



 6
6  [2,3]:
[2,3]:
y1({q4, q7}) = 2, y2({q5, q6}) = 3.
|
|
|
{A2, B6}. |
: |
|
|
|
q1 |
({A2, B6}, q1, 1) |
= 0.1, |
p({A2, B6}, q1, 2) = 0.2, |
|
p({A2, B6}, q1, 3) |
= 0.7; |
|
q2 |
p({A2, B6}, q2, 1) = 1, |
({A2, B6}, q2, 2) = 0; |
|
q 3 |
p({A2, B6}, q3, 1) = 1, |
({A2, B6}, q3, 2) = 0; |
|
q 4 |
p({A2, B6}, q4, 1) = 0, |
({A2, B6}, q4, 2) = 1; |
|
q 5 |
p({A2, B6}, q5, 1) = 0, |
p({A2, B6}, q5, 2) = 0, |
|
|
({A2, B6}, q5, 3) = 1; |
|
|
q6 |
p({A2, B6}, q6, 1) = 0, |
({A2, B6}, q6, 2) = 0, |
|
|
({A2, B6}, q6, 3) = 1; |
|
|
|
148 |
|
|

q7 |
p({A2, B6}, q7, 1) = 0, |
({A2, B6}, q7, 2) = 1; |
|
|
q 8 |
p({A2, B6}, q8, 1) = 0, |
({A2, B6}, q8 , 2) = 1; |
|
|
q 9 |
p({A2, B6}, q9, l) = 1/3, |
({A2, B6}, q9, 2) |
= 2/3; |
|
q 10 |
p({A2, B6}, q10, 1) = 0, |
({A2, B6}, q10, 2) = 1; |
|
|
q 11 |
p({A2, B6}, q11, 1) = 0, |
({A2, B6}, q11, 2) |
= 1. |
|
|
{A i, Bj} |
|
; tk |
|
, |
|
; q1, , qr |
, |
|
|
. |
({Ai, Bj}, tk) |
- |
|
, |
|
tk, |
|
- |
|
{Ai, Bj}. |
|
|
|
|
|
|
|
|
({Ai, Bj}, tk) = |
({Ai , B j}, qs , a s(t k )), |
s |
1,.., r |
qs 











 ,
, 











 -
-




 , as(tk )
, as(tk ) 





 ,
, 











 qs ,
qs , 







 t k .
t k .
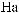


 ,
, 














 {A2, B6},
{A2, B6},








 ,
, 
 ({A2, B6}, t1) =
({A2, B6}, t1) =
= ({A2, B6}, q1, 1) ·
({A2, B6}, q1, 1) · ({A2, B6}, q2, 1) ·
({A2, B6}, q2, 1) · ({A2, B6}, q5, 1) = = 0.1 · 1· 0 = 0;
({A2, B6}, q5, 1) = = 0.1 · 1· 0 = 0;
 ({A2, B6}, t2) =
({A2, B6}, t2) =
= ({A2, B6}, q1, 1) ·
({A2, B6}, q1, 1) · ({A2, B6}, q2, 1) ·
({A2, B6}, q2, 1) · ({A2, B6}, q5, 2) =
({A2, B6}, q5, 2) =
=0.1 · 1 · 0 = 0;
P({A2, B6}, t3) =
= ({A2, B6}, q1, 1) ·
({A2, B6}, q1, 1) · ({A2, B6}, q2, 1) ·
({A2, B6}, q2, 1) · ({A2, B6}, q5, 3) = = 0.1 · 1 · 1 = 0.1;
({A2, B6}, q5, 3) = = 0.1 · 1 · 1 = 0.1;
P({A2, B6}, t4) =
= ({A2, B6}, q1, 1) ·
({A2, B6}, q1, 1) · ({A2, B6}, q2, 2) ·
({A2, B6}, q2, 2) · ({A2, B6}, q6, 1) = = 0.1 · 0 · 0 = 0;
({A2, B6}, q6, 1) = = 0.1 · 0 · 0 = 0;
P({A2, B6}, t5) =
= ({A2, B6}, q1, 1) ·
({A2, B6}, q1, 1) · ({A2, B6}, q2, 2) ·
({A2, B6}, q2, 2) · ({A2, B6}, q6, 2) = = 0.1 · 0 · 0 = 0;
({A2, B6}, q6, 2) = = 0.1 · 0 · 0 = 0;
149

P({A2, B6}, t6) =
= ({A2, B6}, q1, 1) ·
({A2, B6}, q1, 1) · ({A2, B6}, q2, 2) ·
({A2, B6}, q2, 2) · ({A2, B6}, q6, 3) = = 0.1 · 0 · 1 = 0;
({A2, B6}, q6, 3) = = 0.1 · 0 · 1 = 0;
P({A2, B6}, t7) =
=  ({A2, B6}, q1, 2) ·
({A2, B6}, q1, 2) · ({A2, B6}, q3, 1) = 0.2 · 1 = 0.2;
({A2, B6}, q3, 1) = 0.2 · 1 = 0.2;
P({A2, B6}, t8) =
= ({A2, B6}, q1, 2) ·
({A2, B6}, q1, 2) · ({A2, B6}, q3, 2) ·
({A2, B6}, q3, 2) · ({A2, B6}, q7, 1) =
({A2, B6}, q7, 1) =
=0.2 · 0 · 0 = 0;
P({A2, B6}, t9) =
= ({A2, B6}, q1, 2) ·
({A2, B6}, q1, 2) · ({A2, B6}, q3, 2) ·
({A2, B6}, q3, 2) · ({A2, B6}, q7, 2) = = 0.2 · 0 · 0 = 0;
({A2, B6}, q7, 2) = = 0.2 · 0 · 0 = 0;
P({A2, B6}, t10) =
=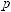 ({A2, B6}, q1, 3) ·
({A2, B6}, q1, 3) · ({A2, B6}, q4, 1) ·
({A2, B6}, q4, 1) · ({A2, B6}, q8, 1) =
({A2, B6}, q8, 1) =
=0.7 · 0 · 0 = 0;
P({A2, B6}, t11) =
= ({A2, B6}, q1, 3) ·
({A2, B6}, q1, 3) · ({A2, B6}, q4, 1) ·
({A2, B6}, q4, 1) · ({A2, B6}, q8, 2) = = 0.7 · 0 · 1 = 0;
({A2, B6}, q8, 2) = = 0.7 · 0 · 1 = 0;
P({A2, B6}, t12) =
= ({A2, B6}, q1, 3) ·
({A2, B6}, q1, 3) · ({A2, B6}, q4, 2) ·
({A2, B6}, q4, 2) · ({A2, B6}, q9, 1)
({A2, B6}, q9, 1)  ({A2, B6}, q10, 1) = 0.7 · 1 · 1
({A2, B6}, q10, 1) = 0.7 · 1 · 1 3 · 0 = 0;
3 · 0 = 0;
P({A2, B6}, t13) =
= ({A2, B6}, q1, 3) ·
({A2, B6}, q1, 3) · ({A2, B6}, q4, 2) ·
({A2, B6}, q4, 2) · ({A2, B6}, q9, 1)
({A2, B6}, q9, 1)  ({A2, B6}, q10, 2) = 0.7 · 1 · 1
({A2, B6}, q10, 2) = 0.7 · 1 · 1 3 · 1 = 7/30;
3 · 1 = 7/30;
P({A2, B6}, t14) =
= ({A2, B6}, q1, 3) ·
({A2, B6}, q1, 3) · ({A2, B6}, q4, 2) ·
({A2, B6}, q4, 2) · ({A2, B6}, q9, 2 )
({A2, B6}, q9, 2 )  ({A2, B6}, q11, 1) = 0.7 · 1 · 2
({A2, B6}, q11, 1) = 0.7 · 1 · 2 3 · 0 = 0;
3 · 0 = 0;
P({A2, B6}, t15) =
=  ({A2, B6}, q1, 3) ·
({A2, B6}, q1, 3) · ({A2, B6}, q4, 2) ·
({A2, B6}, q4, 2) · ({A2, B6}, q9, 2)
({A2, B6}, q9, 2)  ({A2, B6}, q11, 2) = 0.7 · 1 · 2
({A2, B6}, q11, 2) = 0.7 · 1 · 2 3 · 1 = 7
3 · 1 = 7 15 .
15 .
150








 ,
, 



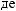











 -
-






 .
.

 ,
, 


 ,
, 












 (1),
(1), 










 [2,1].
[2,1]. 







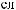

 : 1)
: 1) 
 2)
2) 


 = 1,
= 1, 

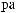





















 = 1,
= 1, 









 ,
, 

 = 2,
= 2, 
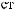






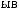


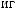












 = 1,
= 1, 









 ,
, 











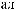





 1-
1-




 -
-




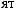



 0.5
0.5  0.5,
0.5, 


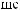










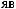









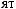




 ,
, 





 ,
,


 .
.
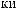




 ,
, 


 :
: 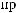

 = 1
= 1 1
1 2
2

 = 2
= 2 1
1 2
2






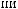
















 .
.





 ,
, 


 :
: 

 = 1
= 1 1
1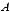 2
2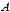 3
3 4
4

 = 2
= 2 1
1 2
2 3
3 4
4 :
:








 [4].
[4].

 4.9.
4.9. {
{




 : {
: { {
{






 :
:



 ,
,









 :
: 




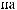 1-
1-




 3
3 






 1
1 
 2.
2. 





 ,
, 












 -
-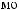






 1-
1-

 (1-2
(1-2 
 3),
3), 









 -
- 















 [
[
 3
3
 . 4.10
. 4.10