Особенности термодинамики растворов полимеров Умеренно концентрированные растворы

Под умеренно концентрированными растворами понимают раство­ры, в которых содержание полимера достаточно для установления одинаковой концентрации звеньев во всем объеме раствора.

Положение граничной области между разбавленным и уме­ренно концентрированным раствором зависит от степени полиме­ризации макромолекул и от природы полимера и растворителя. Для систем, с которыми чаще всего приходится иметь дело на практике такое состояние достигается уже при концентрациях рас­твора, не превышающих единиц процентов.

Отклонение от идеального поведения. В случае растворов низ­комолекулярных веществ в низкомолекулярных растворителях условие H_см= 0 означает их подчинение законам идеальных растворов.

При образовании идеального раствора тепло не выделяется и не поглощается; объем раствора равен сумме объемов компонентов, т. е. V_см=0. Энтропия смешения для идеального раствора пол­ностью определяется числом энергетически эквивалентных микро­состояний, реализуемых путем всех возможных перестановок раз­нородных молекул в системе и называется геометрической или комбинаториальной. Она всегда положительна и равна

S_{см. ид} = – k(N₁ ln Х₁ + N₂ ln Х₂) (2)

где Х₁, Х₂ – мольные доли компонентов;

N₁, N₂ – числа молекул компонентов;

k – постоянная Больцмана.

Растворы полимеров никогда не удовлетворяют всей совокуп­ности этих условий. Они обнаруживают существенные отклонения от идеального поведения даже при H_см = 0. Флори и Хаггинс вывели выражение для комбинаториальной энтропии смешения для атермического раствора модельных гибких цепей в низкомолеку­лярном растворителе:

S_{см. комб.} = – k(N₁ ln ₁ + N₂ ln ₂) (3)

где ₁, ₂ – объемные доли растворителя и полимера.

Формула (3) отличается от формулы (2) тем, что в ней фактически учтен объем полимерной молекулы, который сущест­венно больше объема молекулы растворителя. Следовательно, учет разницы в размерах гибких макромолекул и молекул раствори­теля уже предсказывает отклонение растворов полимеров от иде­ального поведения.

В термодинамике растворов отклонение от идеального поведения (например, от закона Рауля) называют положительным, когда парциальное давление растворителя над раствором больше, чем идеальное. В этом случае G_см. > G_{см. ид}, т. е. компоненты сме­шиваются хуже, чем в идеальном растворе. Отрицательным называют отклонение от закона Рауля, при котором парциальное дав­ление растворителя над раствором меньше, чем идеальное. При этом G_см. < G_{см. ид}, т. е. компоненты имеют сродство друг к другу и смешиваются лучше, чем в идеальном растворе.

Атермический раствор полимера обнаруживает отрицательное отклонение от идеальности, поскольку из сопоставления уравнений (2) и (3) легко показать, что при одинаковой мольной концентрации растворенного вещества S_{см. комб} > S_{см. ид} и, сле­довательно, G_см. < G_{см. ид} .

Однако на самом деле при растворении полимера обычно Н_см.  0 и V_см.  0. В свою очередь, наличие взаимодействия между компонентами приводит к их взаимной координации, и энтропия смешения в такой системе отличается от S_{см. комб}. Для получения выражения для изменения энергии Гиббса при образо­вании реального раствора полимера, т. е. с учетом указанных фак­торов, используют выражение для G_см атермического раствора, в которое вводят дополнительный член, содержащий некоторый безразмерный параметр :

G_см. = RT(n₁ ln ₁ + n₂ ln ₂ + n₁₂) (4)

где R – газовая постоянная;

n₁, n₂ – число молей растворителя и полимера.

Принимают, что параметр  учитывают как энтальпийный, так и энтропийный вклад взаимодействия в G_см .

Из уравнения (4) можно получить выражение для измене­ния химического потенциала растворителя при образовании поли­мерного раствора:

(5)

где z – число звеньев в модельной цепи.

Это соотношение, несмотря на целый ряд допущений, сделанных при его выводе, удовлетворительно объясняет основные закономерности термодинамического поведения гибкоцепных полимеров.

Флори и Ренер провели теоретическое рассмотрение процесса набухания полимера сетчатого строения. Набухание такого полимера происходит до тех пор, пока осмотическая сила растворителя, проникающего в фазу полимера, не уравновесится упругой силой полимерной сетки. Поглощение растворителя набухающим полимером сопровождается увеличением энтропии растворителя за счет смешения его с полимером и уменьшением энтропии полимера из-за распрямления его цепей. Для изменения химического потен­циала растворителя при набухании полимера сетчатого строения было получено выражение

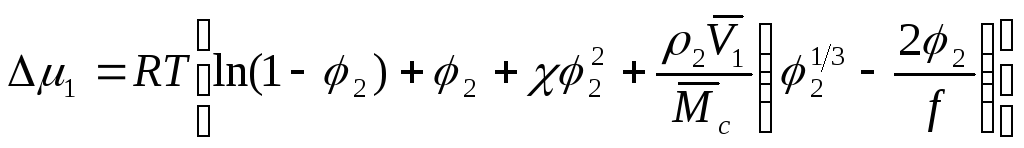
где ₂ – объемная доля полимера в набухшем образце;

₂ – плотность полимера;

–парциальный мольный объем растворителя;

f – функциональность сетки (обычно принимают, что сетка тетрафункциональна, f = 4, т. е. каждый отрезок цепи ограничивается двумя узлами сетки);

–молекулярная масса отрезков цепей между соседними узлами пространственной сетки.

Учитывая, что в равновесии ₁ = 0, и зная параметр взаимо­действия  (хи) можно определить :

(6)

Уравнение состояния полимера в растворе. Уравнением состоя­ния называется уравнение, связывающее давление, объем, темпе­ратуру, концентрацию и другие параметры системы, находящейся в равновесии. В общем виде это уравнение можно записать так: f(Р, T, V, ...) = 0.

В случае раствора полимера уравнение состояния связывает осмотическое давление с температурой, концентрацией раствора и индивидуальными характеристиками компонентов. Осмотическое давление раствора  связано с изменением химического потенциала растворителя соотношением ; поэтому, учиты­вая уравнение (5), можно получить уравнение состояния рас­твора полимера:

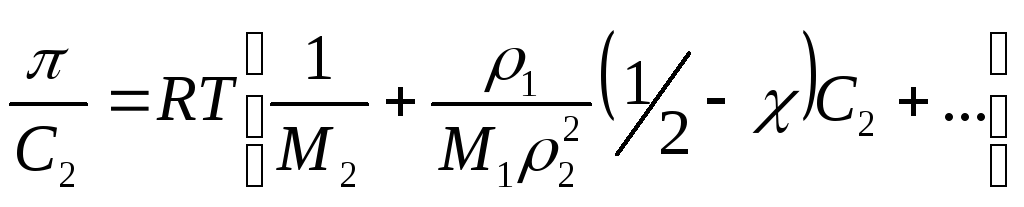(7)

где С₂ – концентрация полимера;

₁ – плотность растворителя;

М₁, М₂ – молекулярные массы растворителя и полимера.

Измеряя зависимость  от С₂ и строя ее в координатах уравнения (7), можно определить значение М₂. Уравнение (7) представляет собой частный случай вириального разложения.

В общем виде:

где А₁ и А₂ – вириальные коэффициенты.

Второй вириальный коэффициент учитывает отклонение раствора полимера от идеального поведения. При А₂=0 уравнение (7) превращается в уравнение Вант-Гоффа для идеального раствора:

.

Коэффициент А₂ определяют по тангенсу угла наклона зависимости приведенного осмотического давления от концентрации раствора (рисунок 3). В выражение для А₂ входит параметр взаимодействия полимер –растворитель . Поэтому коэффициент А₂ существенно зависит от природы растворителя и, поскольку он при достаточно малых кон­центрациях полимера не зависит от концентрации, является удоб­ной характеристикой термодинамического качества растворителя, т. е. термодинамического сродства компонентов раствора.

-состояние раствора полимера. В хороших растворителях А₂ > 0, в плохих А₂ < 0 (см. рис. 6). Из уравнения (7) сле­дует, что А₂ обращается в 0 при  = 0,5.

Как уже отмечалось, параметр  характеризует энергию взаи­модействия Гиббса, т. е. учитывает как тепловые, так и ориентационные эффекты растворения. Поэтому  можно представить в виде двух составляющих – энтальпийного (k₁) и энтропийного (₁ – пси):

(8)

Здесь параметр имеет размерность температуры и на­зывается (тэта)-температурой. Подставив (8) в (7), по­лучим для А₂:

Отсюда видно, что при Т =  коэффициент А₂ = 0, т. е. раствор полимера ведет себя как идеальный. -температуру можно опре­делить, экстраполируя зависимость А₂ от температуры к А₂ = 0.

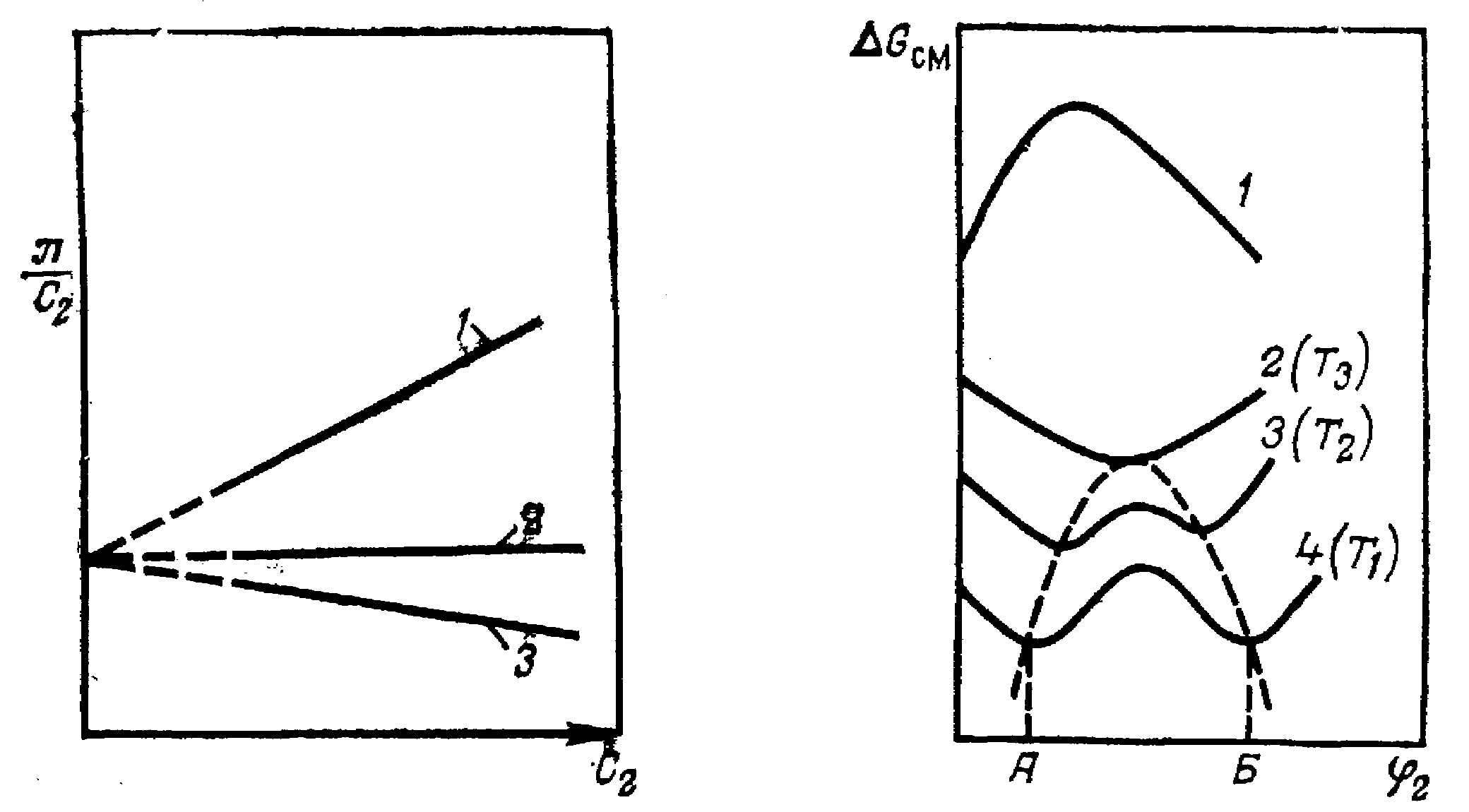
Рисунок 6 – Зависимость приведенного осмотического давления раствора полимера от концентрации раствора С₂:

1 – в хорошем растворителе, А₂ > 0; 2 – в -растворителе, А₂ =0; 3 – в плохом раствори­теле, А₂ < 0.

Рисунок 7 – Зависимость G_см системы полимер – растворитель от объемной доли полимера:

1 – компоненты не смешиваются; 2 – компоненты смешиваются во всех соотношениях; 3, 4 – компоненты частично смешиваются (Т₁ < Т₂ < Т₃).

Состояние, в котором А₂ = 0, называется -состоянием, а рас­творители, в которых оно может быть реализовано, называются  (тэта)-растворителями.

Таким образом, в -состоянии, т. е. при -температуре в -рас-творителе, раствор полимера формально подчиняется законам идеальных растворов. Однако в отличие от растворов низкомоле­кулярных веществ это состояние для каждой данной системы реа­лизуется лишь в определенных температурных точках. Поэтому его правильнее называть псевдоидеальным.

Изменение энергии Гиббса любого реального раствора можно представить в виде двух слагаемых:

G_см = G_{см. ид.} + G_см^Е

где G_см^Е – избыточное изменение энергии Гиббса, учитывающее отклонение от идеального поведения.

При G_см^Е > 0 наблюдается положительное отклонение от иде­альности, при G_см^Е < 0 – отрицательное. В свою очередь:

G_см = H_см. – TS_см^Е

где S_см^Е – избыточное изменение энтропии.

Строго говоря, раствор называется идеальным при условии G_см^Е= 0, H_см. = 0 и S_см^Е = 0. Для растворов полимеров эти условия, как уже отмечалось, в совокупности никогда не реали­зуются. Однако поведение реального раствора описывается урав­нениями для идеальных систем также и в том случае, если усло­вие G_см^Е = 0 выполняется за счет взаимной компенсации энталь-пийного и энтропийного слагаемых, т. е. H_см. = S_см^Е. Для рас­творов полимеров, равно как и для всех реальных газов и растворов, в принципе существует некоторая температура , при которой система ведет себя, как идеальная. Все расчеты при этом значительно упрощаются.

Фазовые равновесия. В растворе полимера, как и во всякой однофазной молекулярно-дисперсной системе, всегда имеют мест гомофазные флуктуации концентрации. В определенных условиях могут возникнуть гетерофазные флуктуации, которые являются зародышами новой фазы и при небольшом изменении условий превращаются в новую пространственно протяженную фазу. В результате однофазный раствор разделяется на две фазы, одна из которых представляет собой более разбавленный, а другая – более концентрированный раствор по сравнению с исходным. Такие фазовые превращения характеризуются соответствующими изменениями термодинамических функций.

Флуктуáция, флюктуáция – [<лат. fluctuatio колебание] – случайное отклонение величины, характеризующей систему из большого числа частиц, от его среднего значения; например, временное, случайное отклонение от равномерного распределения молекул в газе или жидкости, возникающее в результате теплового движения.

Компоненты смешиваются во всех соотношениях, когда G_см < 0 для любого состава раствора (рисунок 7). Если компоненты совсем не смешиваются, то G_см > 0, и система двухфазна во всей области составов, причем каждая фаза представляет собой чистый компонент. Если же компоненты смешиваются частично, то в области составов, где они не смешиваются (участок АБ на рисунке 7), сосуществуют две фазы, состав которых определяется общей касательной к двум минимумам на кривой зависимости G_см от состава. В остальной области составов система однофазна. Взаимная смешиваемость компонентов существенно зависит от температуры. Например, для многих систем область ограниченной растворимости компонентов уменьшается с повышением темпера­туры, и при некоторой температуре (Т₃ на рисунке 7) наблюдается полная смешиваемость. Эта температура и является верхней кри­тической температурой растворения. Соединив плавной кривой точки, отвечающие составам фаз, находящихся в равновесии при разных температурах и ВКТР, получим диаграмму состояния системы полимер – растворитель (так называемую бинодаль). При температуре Т₁ (см. рисунок 7) зависимость G_см от состава имеет два минимума и один максимум. С повышением темпера­туры все эти точки сближаются, пока не сольются в одну точку. Поэтому критической температуре соответствуют равенства:

Используя выражение (4), находят критическое значение параметра . Его подставляют в уравнение (8) и, решая послед­нее уравнение относительно Т_кр, получают:

(9)

где Р – степень полимеризации полимера.

Таким образом, критическая температура растворения полимера зависит от степени полимеризации, т. е. от молекулярной масс полимера и с увеличением молекулярной массы смещается сторону более высоких температур и меньших концентраций раствора (рисунок 8).

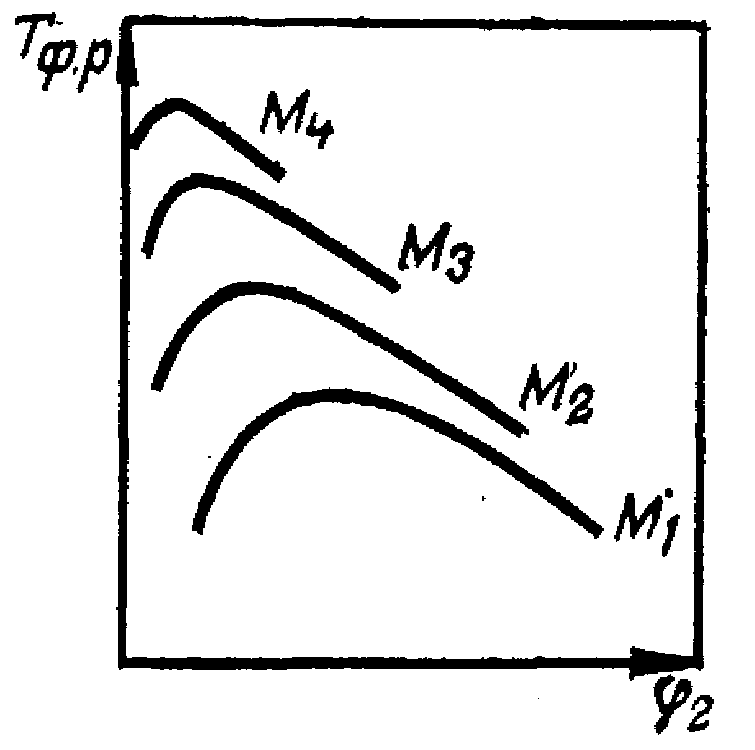
Рисунок 8 – Зависимость температуры фазового расслоения системы полимер – растворитель от объемной доли полимера разных молекулярных масс (М₁ < М₂ < М₃ < М₄).

Уравнение (9) получено на основе теории Флори – Хаггинса, которая в силу несовершенства некоторых исходных посылок предсказывает существование только одной критической температуры, а именно ВКТР; поэтому в данном случае речь идет о вктр.

На основании уравнения (9) можно дать еще одно определение -температуры как верхней критической температуры растворения полимера бесконечно большой молекулярной массы.

Если система полимер – растворитель обладает и ВКТР и НКТР, то ей должны быть свойственны две -температуры (рисунок 9, а).

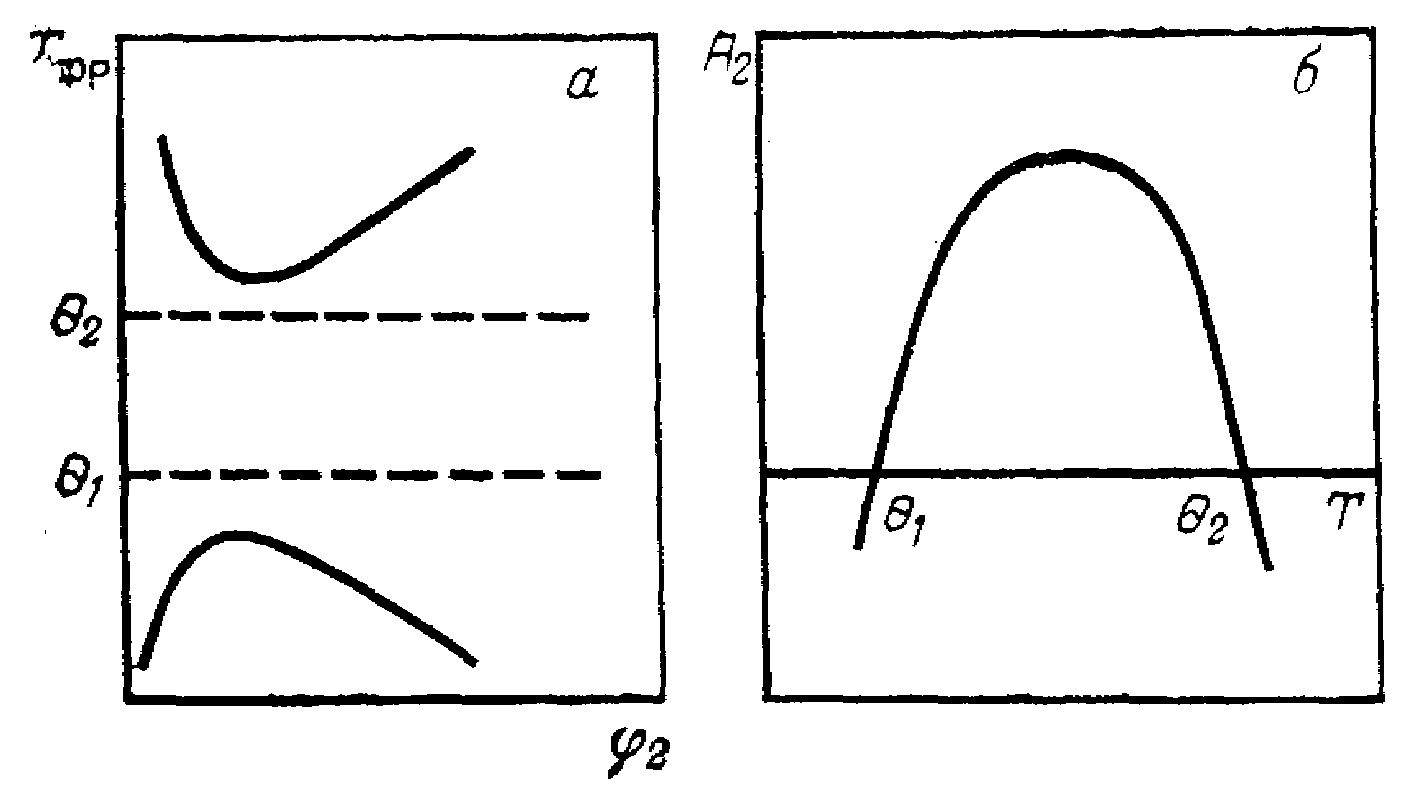
Рисунок 9 – Зависимость температуры фазового расслоения системы полимер – растворитель от объемной доли полимера (а) и второго вириального коэффициента раство­ра полимера от темпера­туры (б).

При этом качество растворителя, о котором можно судить по коэффициенту А₂, будет изменяться по кривой с макси­мумом в зависимости от температуры (рисунок 9, б). В области между ₁ и ₂, где данный растворитель является для полимера хорошим, растворы полимеров обнаруживают отрицательное от­клонение от идеальности (G_см^Е < 0), тогда как при температурах ниже ₁ и выше ₂ растворитель является плохим, и отклонение от идеальности становится положительным. С увеличением молеку­лярной массы полимера ВКТР повышается, а НКТР снижается. Поэтому для полимера одной и той же молекулярной массы кри­тические температуры могут служить мерой качества раствори­теля: чем ниже ВКТР и выше НКТР, тем лучше растворитель, шире область гомогенного раствора.